Высокоскоростной удар — различия между версиями

Версия 13:08, 11 декабря 2019

Курсовой проект по Механике дискретных сред

Исполнитель: Пальчиковская Наталия

Группа: 3630103/60101

Семестр: осень 2019

Постановка задачи

Построить модель взаимодействия ударника и препятствия. Исследовать зависимость глубины проникания в преграду от скорости ударника.

Построение модели

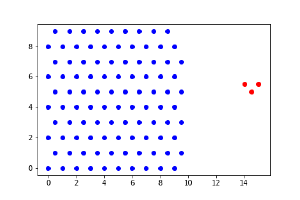
Поскольку задача состоит в исследовании зависимости глубины проникания от скорости ударника, будем рассматривать поперечное сечение преграды. Пусть это сечение представляет собой двумерную область с треугольной кристаллической решеткой(рис.1). Ударник так же моделируем, как некоторую совокупность частиц. (Введенные обозначения показаны на рисунке 2)

Рисунок 1. Модель преграды и ударника

Рисунок 2. Обозначения

Предположим, что все частицы взаимодействуют посредством потенциала Леннарда-Джонса.

Теоретическая сводка

Потенциал Леннарда-Джонса

Парный силовой потенциал взаимодействия. Определяется формулой:

[math] \varPi(r) = D\left[\left(\frac{a}{r}\right)^{12}-\left(\frac{a}{r}\right)^{6}\right], [/math]

где

• [math]r[/math] — расстояние между частицами,
• [math]D[/math] — энергия связи,
• [math]a[/math] — длина связи.

Потенциал является частным случаем потенциала Ми и не имеет безразмерных параметров.

Сила взаимодействия, соответствующая потенциалу Леннард-Джонса, вычисляется по формуле

[math] F(r) = \frac{12D}{a}\left[-\left(\frac{a}{r}\right)^{13} + \left(\frac{a}{r}\right)^{7}\right]. [/math]

Решение

В зависимости от скорости ударника возможны три результата взаимодействия.

• Случай 1:пуля не деформирует преграду
• Случай 2:пуля застревает в преграде
• Случай 3:пуля проходит насквозь преграды

При построении модели были приняты следующие значения параметров:

[math]a=1[/math]

[math]D=1[/math]

[math]m=1[/math]

[math]dt=0.001[/math] -шаг по времени

Тогда скорость диссоциации равна:

[math]Vd= \sqrt{ \frac{2D}{m}}=1.4[/math].

Случай 1

[math]V=0.1 Vd[/math] -скорость ударника

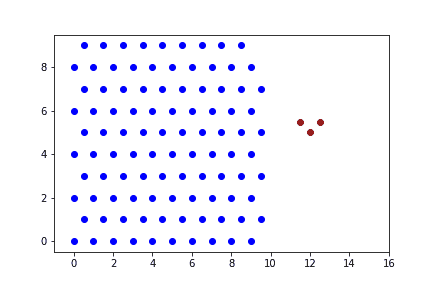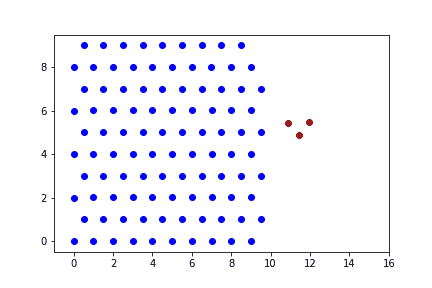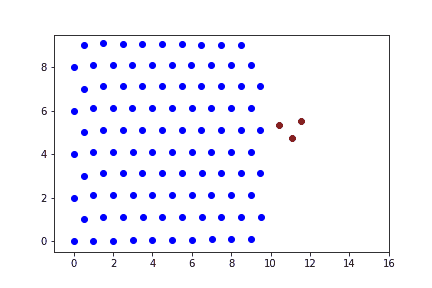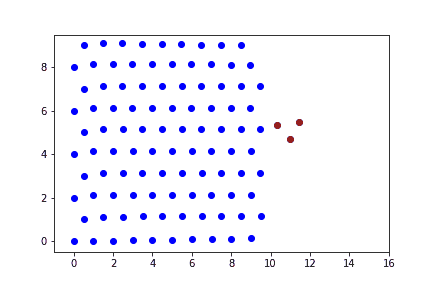
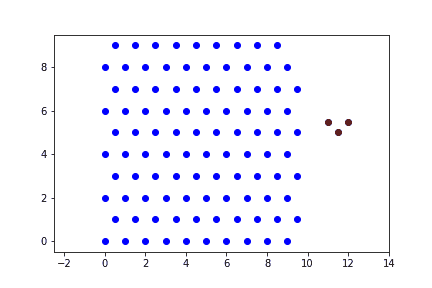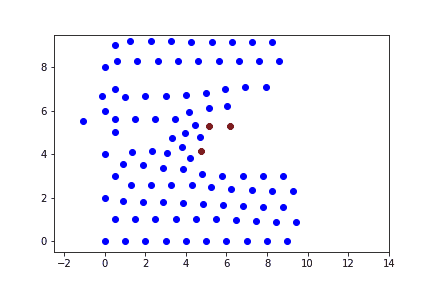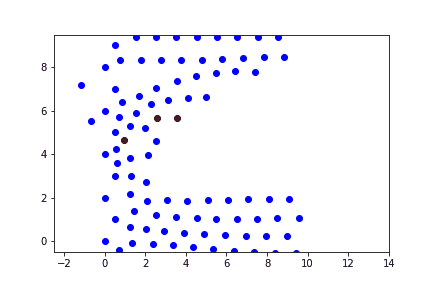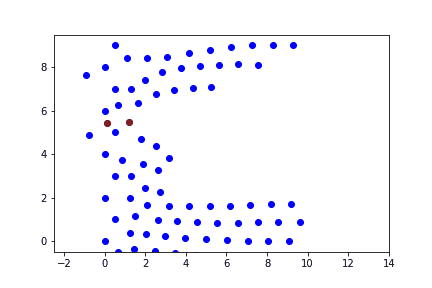
При малых скоростях ударника (не характерных для реальной пули) преграда не деформируется, пуля прилипает к стенке преграды.

Случай 2

[math]V=0.9 Vd[/math]

При малых скоростях пули в результате взаимодействия деформируется препятствие, в нем застревает ударник.

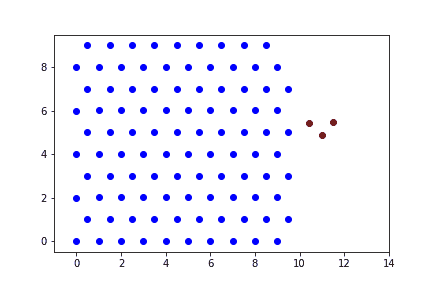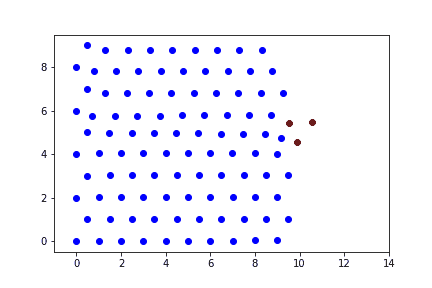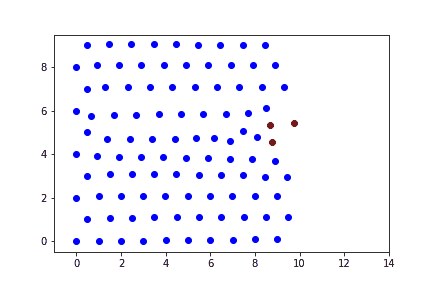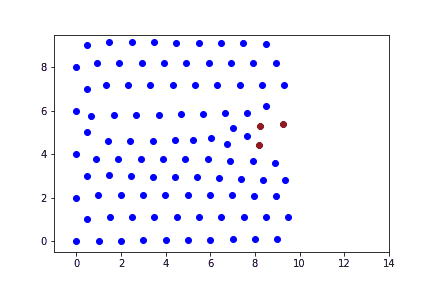
Случай 3

[math]V=10 Vd[/math]

При высоких скоростях ударника наблюдается прохождение пули насквозь препятствия.

См. также

• Метод динамики частиц
• Механика дискретных сред
• Введение в механику дискретных сред
• Виртуальная лаборатория
• Курсовые работы 2012-2013 учебного года
• Курсовые работы 2013-2014 учебного года
• Курсовые работы 2014-2015 учебного года
• Курсовые работы 2016-2017 учебного года