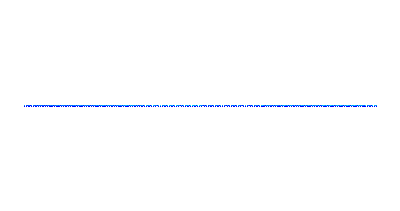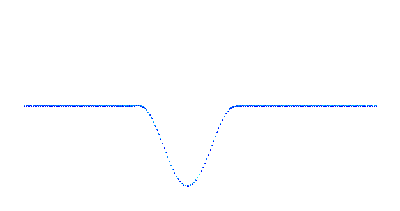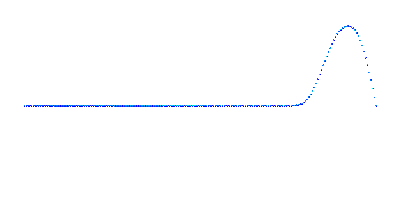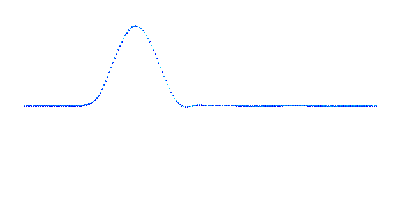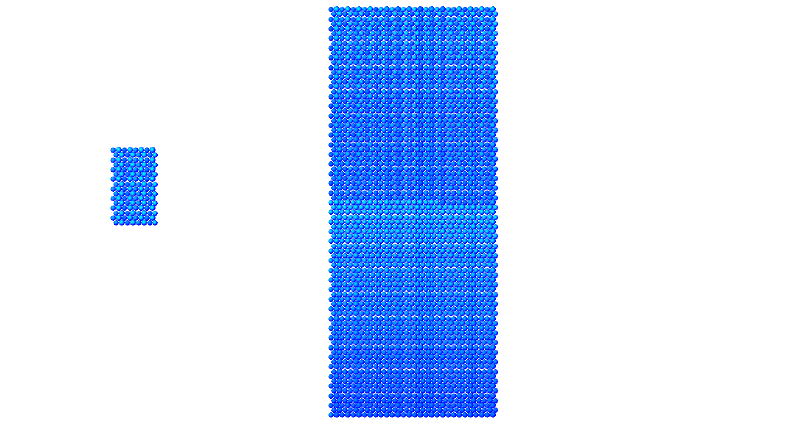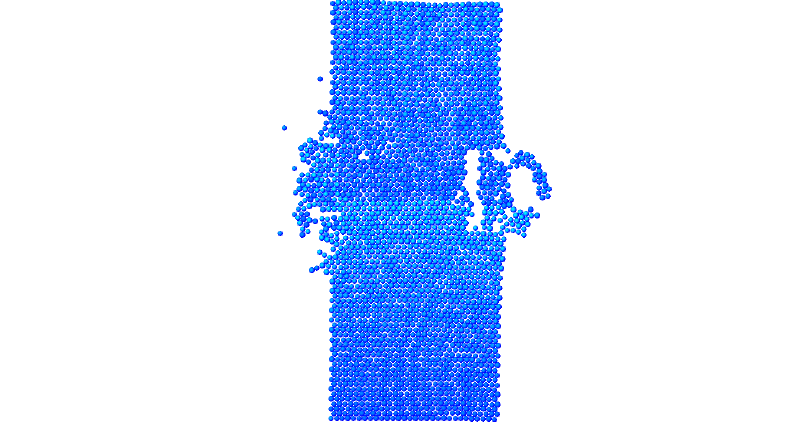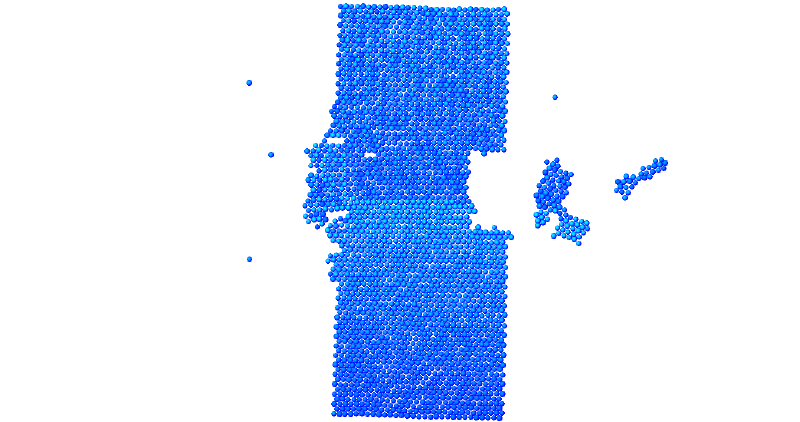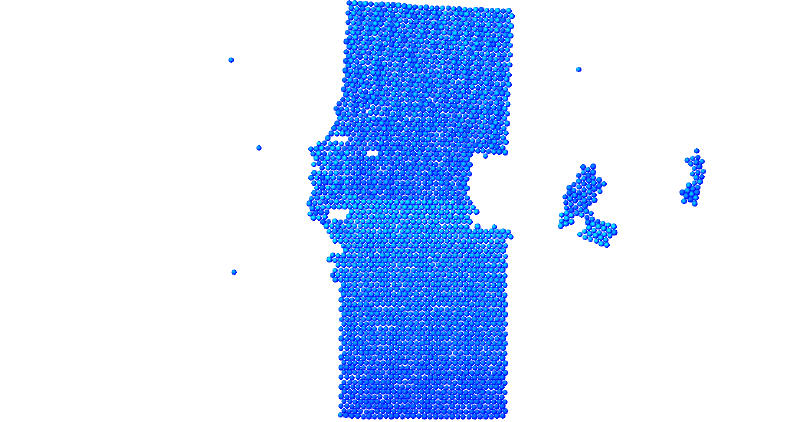Курсовые работы по ТОМДЧ: 2013-2014 — различия между версиями

Текущая версия на 08:38, 31 августа 2015

Введение в механику дискретных сред: курсовые работы 2013-2014

Предмет: "Теоретические основы метода динамики частиц"

Лектор: Виталий Андреевич Кузькин

Группа: 40510

Учебный год: 2013-2014

Семестр: осень 2013

Моделирование распространения поперечных волн в двумерном стрежне[править]

Исполнители:: Степанов Алексей

Рассматривается стержень, имеющий толщину в 1 атом. Взаимодействие между атомами, находящимися на расстоянии меньшем, чем радиус обрезания, описывается законом

[math] \underline{F}(r) = k \frac{\left|\underline{r}\right|-a_{0}}{\left|\underline{r}\right|}\underline{r} [/math]

Здесь, [math]k[/math] — жесткость связи, [math]\underline{r}[/math] — радиус-вектор, соединяющий частицы и [math]a_{0}[/math] равновесное расстояние. Радиус обрезания в работе выбран: [math] r_{cut} = 1.5 [/math].

Было смоделировано несколько различных задач:

• Отражение волны от свободного конца
• Отражение волны от заделанного конца
• Распространение волны без дисперсии
• Распространение волны с дисперсией

Во всех этих задачах, граничный условия на другом конце выглядели так:

[math] \begin{cases} y(t) = A\sin\left(\frac{2\pi t}{T}\right), t \lt \frac{T}{2}\\ F = 0, t \gt \frac{T}{2} \end{cases} [/math]

Результаты:

• Отражение волны от свободного конца

• Отражение волны от заделанного конца

• Распространение волны с дисперсией
• Соударение двух встречных волн

Моделирование распространения продольных волн (MATLAB)[править]

Исполнители: Краморов Данил

Рассматривается бегущая по цепочке частиц продольная волна в разных постановках:

• Волна отражается от свободного конца
• Волна отражается от заделанного конца
• Волна с периодическими граничными условиями
• Волна с дисперсией

Под волной с дисперсией подразумевается рассеивание волны при уменьшении длины волны - по ходу движения за главным пиком вся явнее выражаются побочные.

Результаты:

• Отражение волны от свободного конца

• Отражение волны от заделанного конца

• Волна с периодическими граничными условиями

• Волна с дисперсией

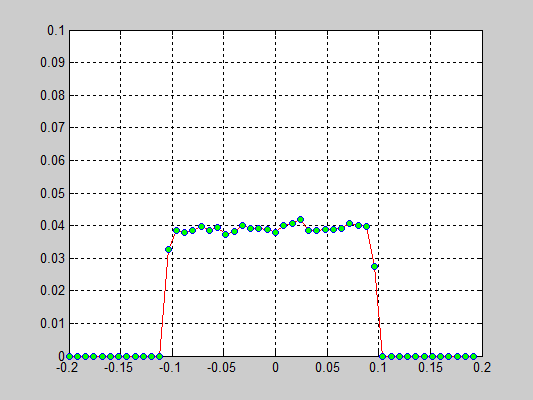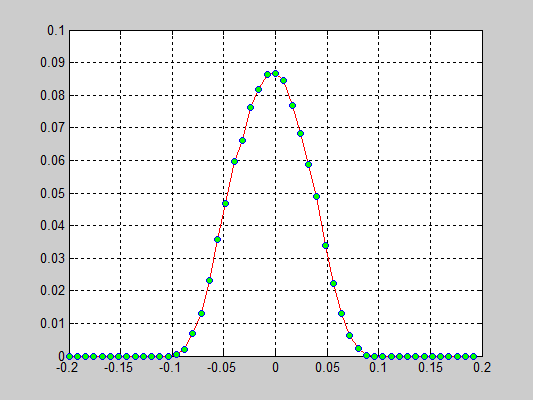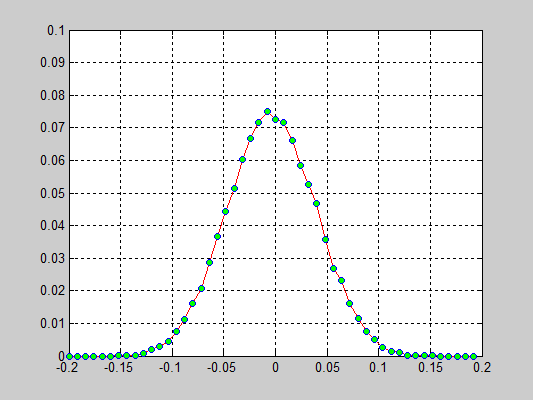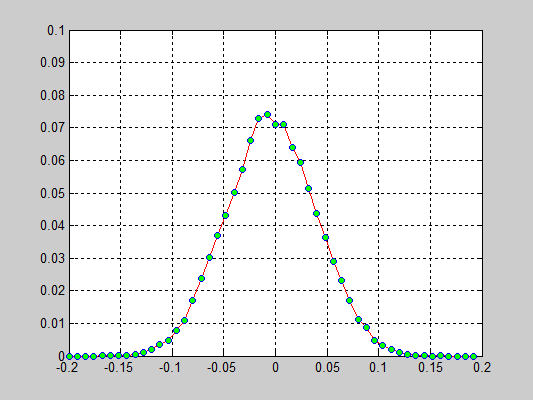
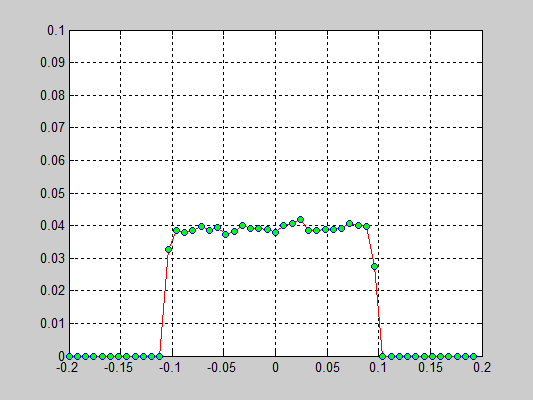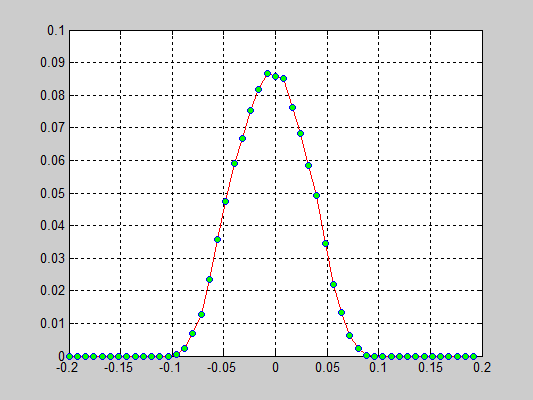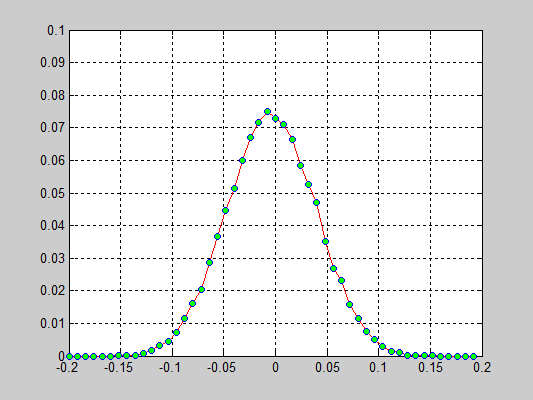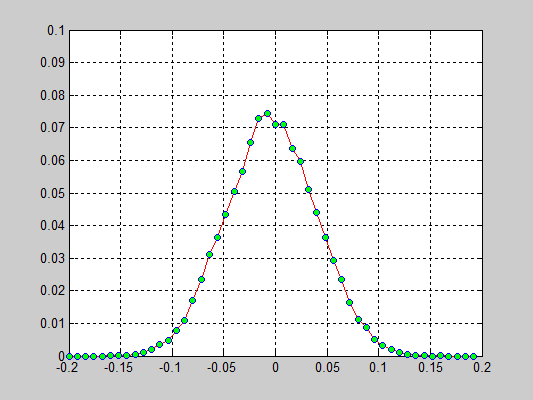
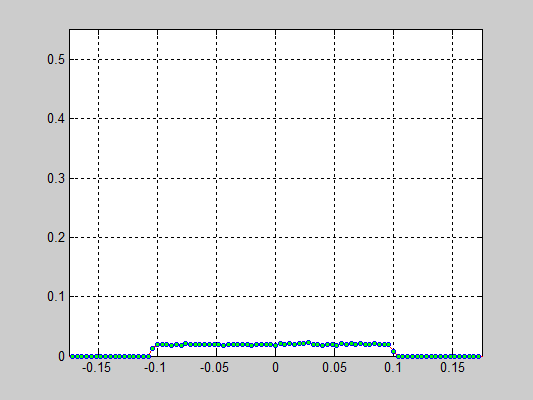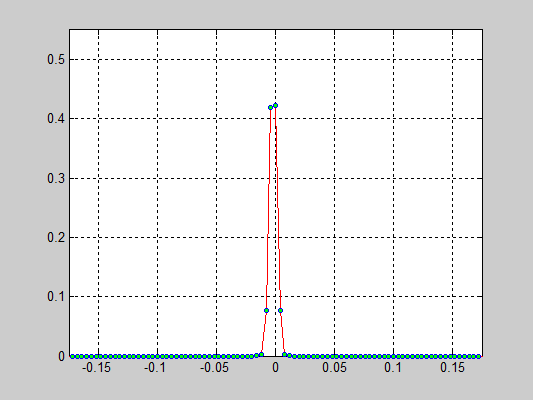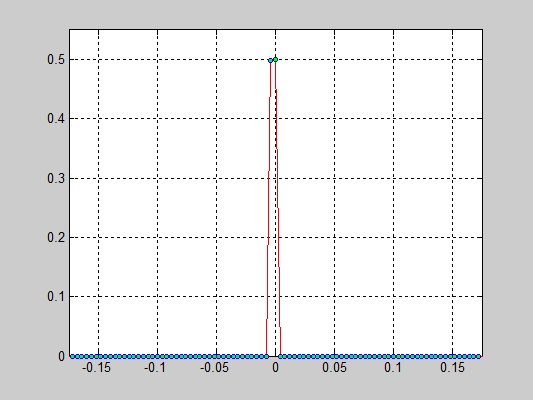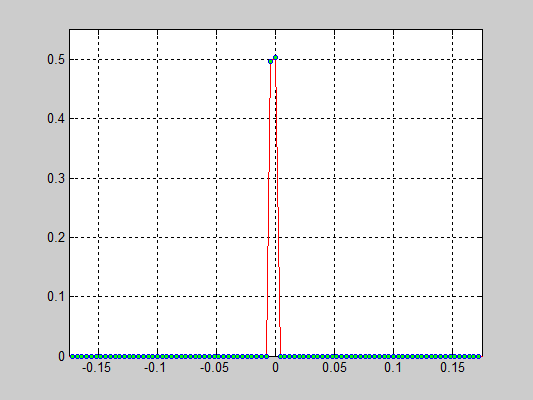
Моделирование цепочки частиц, анализ распределения скоростей[править]

Исполнители: Дзенушко Дайнис

Рассматривается цепочка частиц с периодичными граничными условиями. Задаются начальные скорости частиц, т.е. вводится начальная температура.
Исследуется распределение скоростей частиц от времени. В начальной конфигурации задается равномерное распределение скоростей.

Взаимодействие частиц описывается потенциалом Леннарда-Джонса который записывается в следующем виде:
[math]U(r) = D \left[ \left(\frac{a}{r}\right)^{12} - \left(\frac{a}{r}\right)^{6} \right],[/math]
r — расстояние между центрами частиц
D  — глубина потенциальной ямы
a — равновесное расстояние

Результаты:

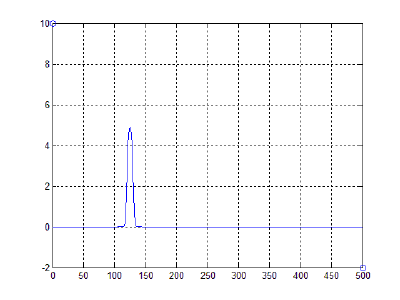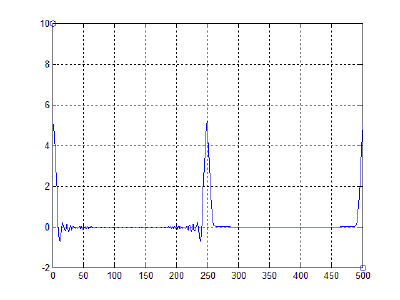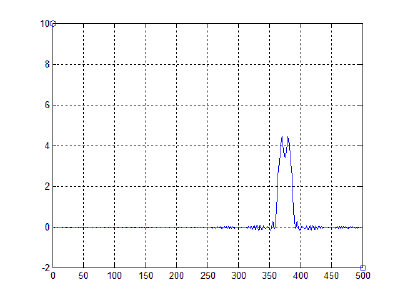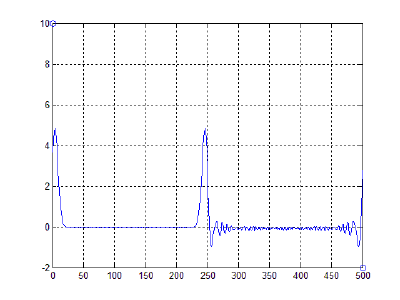
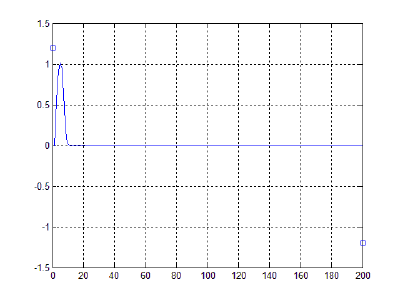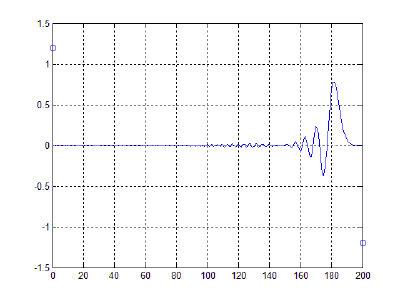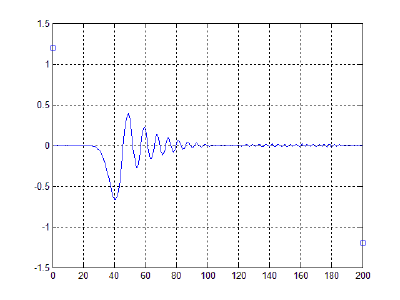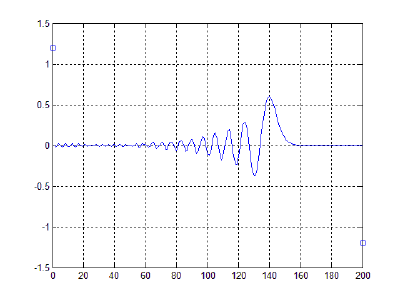
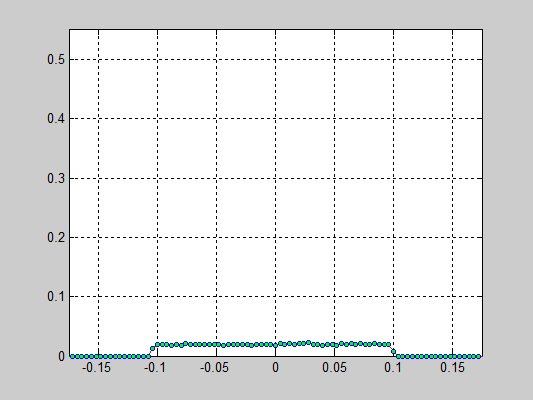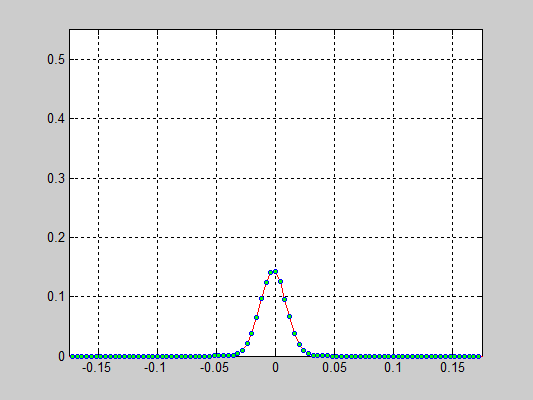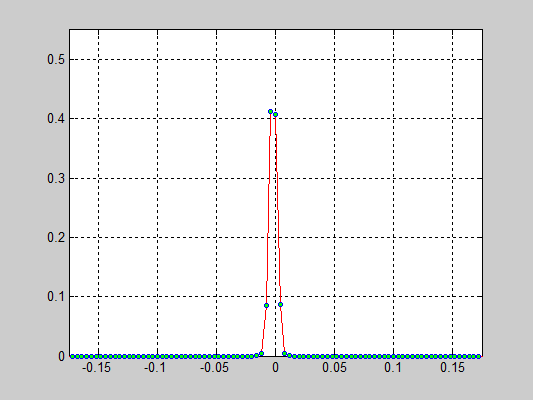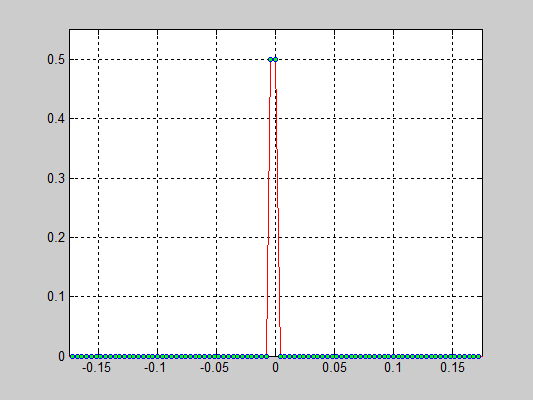
• 40000 частиц, без диссипаций, радиус обрезания a_cut = 1.4 a0 (слева) и 5.1 a0 (справа), максимальные начальные скорости v0 = 0.5 * vo / 6
  

• 40000 частиц, с диссипацией B = 2.6*Bo/100(слева) и B = 5.2*Bo/100(справа), радиус обрезания a_cut = 1.4 a0, максимальные начальные скорости v0 = 0.5 * vo / 6
  

Моделирование выстрела из лука[править]

Исполнители: Фролова Ксения

Постановка задачи:
В данной работе моделируется процесс выстрела из лука с целью получения качественного анализа поведения рассматриваемой механической конструкции. Реализация происходит в среде разработки Code::Blocks.

В реальных моделях плечи лука являются упругими стержнями, а тетива – растяжимой нитью.

Рассматривается плоская задача. В построенной модели плечи лука состоят из двух слоев частиц, находящихся друг от друга на расстоянии, равном равновесному, а тетива - из одного. Снаряд (стрела) также состоит из одного слоя частиц. Для описания взаимодействия между частицами тетивы и стрелы используется потенциал Леннарда - Джонса (1), взаимодействие между остальными частицами определяется законом (2):
[math] U(r) = 4\varepsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^{6} \right], [/math] (1)
[math] \underline{F}(r) = k \frac{\left|\underline{r}\right|-a_{0}}{\left|\underline{r}\right|}\underline{r} [/math] (2)
Где
[math]k[/math] — жесткость связи
[math]\underline{r}[/math] — радиус-вектор, соединяющий частицы
[math]a_{0}[/math] - равновесное расстояние

Примечание: при расстоянии между частицами тетивы и стрелы, превышающим равновесное расстояние, взаимодействие между этими частицами отсутствует.

Радиус обрезания [math] a_{cut} = 1.2 [/math]; жесткость связи [math]k = 2.0[/math].</math>
Частицы, составляющие плечи лука, не взаимодействуют c

• частицами тетивы (за исключением ушек – элемента тетивы, одеваемого на лук)
  
• частицами стрелы
  

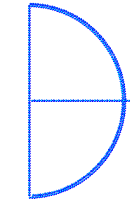
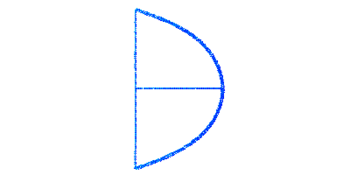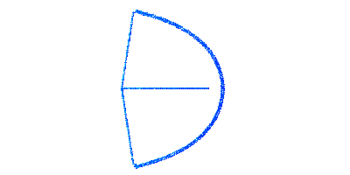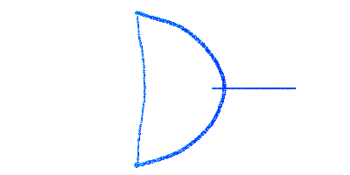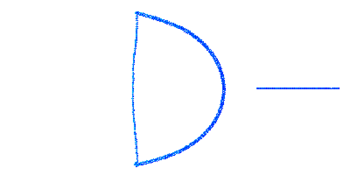
Плечи в недеформированном состоянии представляют собой полуокружность. При натянутой на лук тетиве конструкция находится в равновесии. Сила натяжения лука, приложенная к середине тетивы, задается статически – частица, находящаяся в середине тетивы, перемещается вдоль горизонтальной оси ox на величину [math] s = -0.0012a [/math].
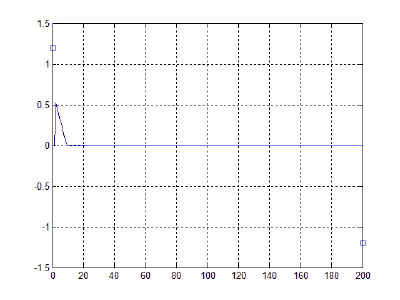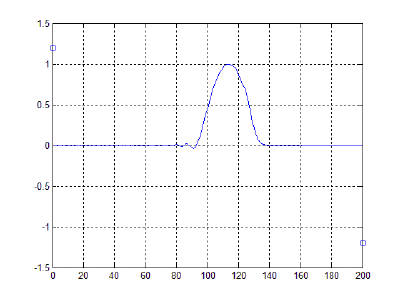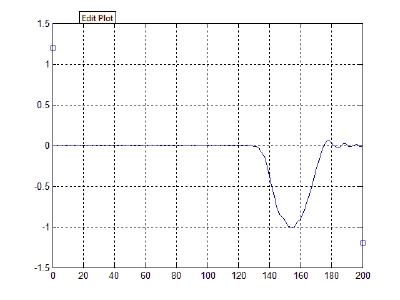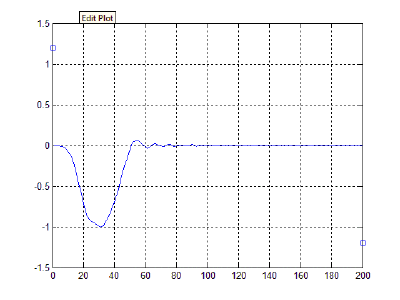
Начальная конфигурация лука представлена на рисунке 1.

• 

  Рисунок 1. Начальная конфигурация лука.

Результат:

• 

  Процесс выстрела из лука

Обсуждение результатов и выводы:
Из полученных результатов видно, что при отпускании тетивы (в момент, когда сила натяжения лука перестает действовать, т.е. частица, являющаяся серединой тетивы, останавливается) энергия, накопленная в деформированных за счет оттягивания тетивы плечах, преобразуется в кинетическую энергию полета стрелы. За счет этого, в свою очередь, и происходит движение снаряда в сторону разгибания дуги, стремящейся вернуться в исходное состояние равновесия системы. Это соответствует принципу действия реальных конструкций.
Замечание:

• Поскольку в модели не учитывается действие силы тяжести, стрела движется не по параболической траектории, как это происходит в реальности, а вдоль горизонтальной оси.
  

Потеря устойчивости стержня[править]

Исполнители:: Пшенов Антон

Рассматривается стержень состоящий из частиц взаимодействующих по потенциалу V-model, подвергающийся сжатию в квазистатической постановке. Граничные условия на концах соответсвуют заделке, тоесть перемещение и вращение крайних частиц равны нулю. Квазистатическая задача предпологает последовательное смещение каждой частицы с определенным интервалом по времени, тем самым обеспечивая сжатие стержня без возникновения значительных продольных волн.

При различных значениях скорости деформации наблюдается потеря устойчивости по разным формам.

• 

  Потеря устойчивости по I форме

• 

  Потеря устойчивости по II форме

• 

  Потеря устойчивости по III форме

• 

  Потеря устойчивости по IV форме

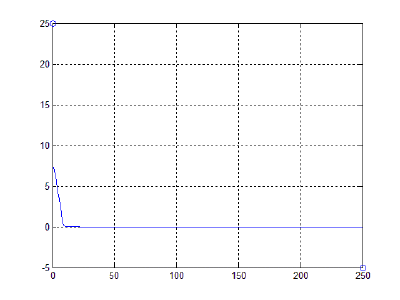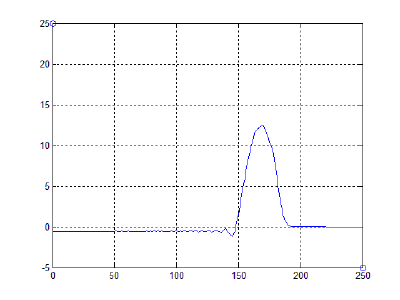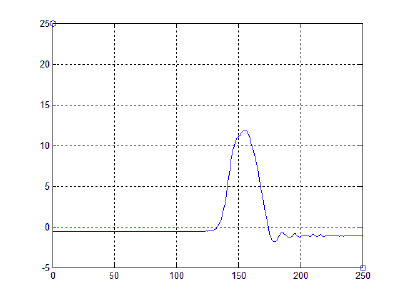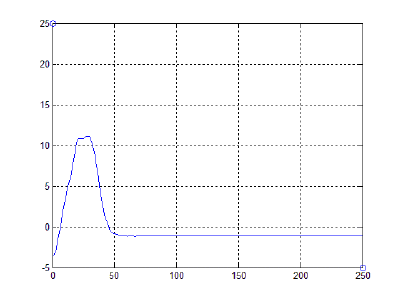
В ходе моделирования замеряется сила действующая на крайнюю частицу, соответствующая нагрузке на стержень. При потере устойчивости наблюдается резкое падение этой силы означающее переход к другому равновесному состоянию.Полученное значение максимальной нагрузки сравнивается с введенной Эйлером критической силой, вычисляющейся по формуле:

[math] P_{k} = \frac{n^{2}\cdot\pi^{2}\cdot EJ}{l^{2}} [/math]

При устремлении скорости деформации к нулю было получено близкое к аналитическому значение критической нагрузки.

Аналогичную задачу можно поставить и для кручения стержня.

• 

  Потеря устойчивости при кручении

Моделирование пробивания пластины шаром[править]

Исполнители: Веренинов Игорь

Рассматривается деформируемый шар пробивающий пластину,толщиной в одну частицу.

Результаты:

• 1000 частиц, радиус обрезания a_cut = 1.4 a0 максимальные начальные скорости v0 = 0.5 * vo / 6
  

Моделирование откольного разрушения в двумерной постановке[править]

Исполнители: Симонов Роман

Рассматривается пластина ,которую ударяет тело размером меньше в 5 раз. При соударении наблюдается откол части пластины схожей по форме с ударяемым телом.

Результаты:

• 2700 частиц, радиус обрезания a_cut = 1.4 a0
  

См. также[править]

• Метод динамики частиц
• Механика дискретных сред
• Теоретические_основы_метода_динамики_частиц
• Курсовые работы 2011-2012 учебного года
• Курсовые работы 2012-2013 учебного года