V-model

Department "Theoretical Mechanics" > Adminstration > V.A. Kuzkin > V-model

---

A model for elastic bonds in solids (EVM)

SEM image of composite consisting of nanoparticles bonded by a copolymer. (N. Preda, et. al., Mater. Res. Bull. 45, 1008 (2010))

Introduction

The article is based on the papers:

• V.A. Kuzkin and I.E. Asonov "Vector-based model of elastic bonds for simulation of granullar solids"// Phys. Rev. E, 86, 051301, 2012 (download author's version, pdf).
• Kuzkin V.A., Krivtsov A.M. Enhanced vector-based model for elastic bonds in solids // Letters on materials 7 (4), 2017, pp. 455-458 (download ArXiv version)

The Discrete (or Distinct) Element Method (DEM) is widely used for the computer simulation of solid and free-flowing granular materials. Similarly to classical molecular dynamics, in the framework of DEM the material is represented by a set of many interacting rigid body particles (granules). The equations of the particles' motion are integrated numerically. In free-flowing materials the particles interact via contact forces, dry and viscous friction forces, electrostatic forces, etc. Computer simulation of deformation and fracture of granular solids, such as rocks, concrete, ceramics, particle compounds, agglomerates, nanocomposites, etc. is even more challenging. Particles in granular solids are usually connected together by some additional bonding material such as cement or glue. The example of composite material consisting of PbS nanoparticles bonded together by a copolymer is shown in figure above. The copolymer (bonding material) resists the relative translation and rotation of neighboring PbS particles. In DEM simulations bonding material is usually taken into account implicitly using the concept of so-called bonds. Neighboring particles are connected by the bonds that resist to stretching/compression, shear, bending, and torsion. The bonds cause forces and torques acting on the particles along with contact forces. Mass of the bonding material is usually neglected. The assumption does not influence static properties of the granular material. The influence on the dynamic properties is not so straightforward and should be considered separately. However let us note that in many practical applications the mass of bonding material is much smaller than the mass of the particles (see, for example, figures below). Therefore the mass of bonding material can be neglected.

Discrete Rod: SEM image of 1D assembly of particles embedded in polymer matrix (M. Wang, et.al., Materials Today, Vol. 16, No. 4, 2013)

Discrete Shell: Colloidsome composed of polysterene spheres (A.D. Dismore, et.al. Science, 2002)

Discrete Solid: aerogel (source)

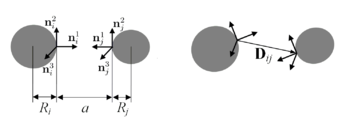
In the paper V.A. Kuzkin and I.E. Asonov "Vector-based model of elastic bonds for simulation of granullar solids"// Phys. Rev. E, 86, 051301, 2012 vector-based model(the V-model) of elastic bonds in solids is developed. The V-model is based on the combination of approaches proposed in works of P.A. Zhilin, E.A. Ivanova, A.M. Krivtsov, N.F. Morozov , and works of M.P. Allen , S.L Price. Equations describing interactions between two rigid bodies in the general case are summarized. The general expression for the potential energy of the bond is represented via vectors rigidly connected with bonded particles (see figures below).

Vectors connected with the particles

Different deformations of the bond.

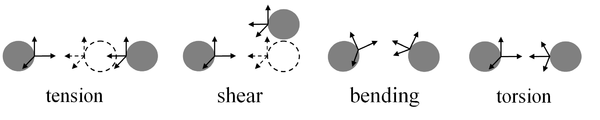
The vectors are used for description of different types of bond's deformation. The expression for potential energy corresponding to tension/compression, shear, bending, and torsion of the bond is proposed. Forces and torques acting between particles are derived from the potential energy. Two approaches for calibration of V-model parameters for bonds with different length/thickness ratios are presented. Simple analytical formulas connecting geometrical and elastic characteristics of the bond with parameters of the V-model are derived. Main aspects of numerical implementation of the model are discussed.

Advantages of the V-model

Let us summarize advantages of V-model:

• longitudinal, shear, bending, and torsional stiffnesses of the bond are independent
• applicable in the case of large turns of the particles
• conservation of energy (bonds are perfectly elastic)
• any non close packed structure, rods and shells can be simulated(see figures above)
• forces and torques are calculated as a functions of particles' positions and orientations (more accurate integration of motion equations than in the case of incremental algorithm used for BPM)
• description of bonds of any length/thickness ratio. It is shown that in the case of small deformations the behavior of the bond can fit the behavior of Bernulli-Euler rod or Timosheko rod or short cylinder connecting particles (depending on length/thickness ratio)
• simple analytical expressions connecting parameters of V-model with geometrical and mechanical characteristics of the bond
• bonds can connect points inside the particles or lying on particles surfaces (not only particle centers)
• fracture criterion for the bond can be used if required

Java Script example

Two dimmensional example: deformation of a discrete rod. Author: Ruslan Lapin

Pull the last particle using mouse.

Some examples

Press the links under the picture to see the animation.

• 

  Buckling of the discrete rod under the action of following force

• 

  Instability of a discrete rod under torsion

• 

  Rod under the action of following torque (Nikolai paradox)

• 

  Torsion of the wire

• 

  Discrete plate under the action of following shear force

• 

  Residual stresses in a discrete plate

• 

  Buckling of the discrete hemisphere

• 

  Discrete spherical shell bouncing between rigid walls

• 

  Discrete spherical shell impacting rigid walls

Debugging

The simplest way of debugging is a solution of the following four test problems for the system of 2 bonded particles. In all four cases forces and torques acting on the particles can be calculated both analytically and numerically. Obviously, the results should coincide.

• Pure stretching. Porition of one particle is fixed. Another particle is moving along the line connecting particles with constant velocity. The force acting on the particles is calculated.
• Pure shear. Orientations of the particles are fixed. Position of one particle if fixed. Another particle is moving (with constant velocity) along the line, orthogonal to initial direction of the bond. The force and torques acting on the particles are calculated.
• Pure bending. Positions of both particles are fixed and the particles are rotated along the same axis, orthogonal to the bond, but in opposite directions. The torque acting on the particles is calculated.
• Pure torsion. Positions of both particles are fixed. Orientation of one particle is fixed. Another particle is rotating around the bond. The torque acting on the particles is calculated.

DEM packages using the V-model

• LIGGGHTS, details of implementation and some examples are given here.
• WaLBerla (implemented by Igor Ostanin and Vitaliy Petrov from Skoltech)

History and acknowledgements

The idea underlining V-model was first formulated by Vitaly Kuzkin during communication with Michael Wolff in Technical University of Hamburg (March, 2011). The first formulation was very simple and coarse, but it works! The results of some test simulations were presented by Vitaly Kuzkin on APM 2011 conference (July, 2011). At the present moment V-model is much more flexible and physically meaningful than its first version. Now it is developed jointly by Vitaly Kuzkin and Igor Asonov. The V-model is implemented in DEM package LIGGGHTS by Patrick Fodor.

The authors are deeply grateful to Michael Wolff, Prof. Anton Krivtsov, Prof. Stephan Heinrich, Dr. Sergiy Antonyuk and Prof. William Hoover.

Links

• Implementation_of_V_model_in_LIGGGHTS
• Vitaly Kuzkin
• Igor Asonov
• Selected publications of Vitaly Kuzkin