"Распространение тепла в кристалле со случайными перемещениями и нулевыми скоростями"
Курсовой проект по Механике дискретных сред
Исполнитель: Полинов Михаил
Группа: 3630103/60101
Семестр: осень 2019
Постановка задачи[править]
1) Реализовать распространение тепла в одномерном кристалле со случайными перемещениями и нулевыми скоростями в начальный момент времени
2) Сравнить с распространением тепла в одномерном кристалле со случайными скоростями и нулевыми перемещениями в начальный момент времени
Построение модели[править]
Рассмотрим одномерный кристалл: цепочку одинаковых частиц массы m, соединенных одинаковыми линейными пружинами с жесткостью C.
Уравнения динамики кристалла имеют вид:
где - перемещение -й частицы; - индекс, принимающий произвольные целые значения, - жесткость связи между частицами, - масса частицы.
Кинетическая температура T определяется как:
, где — постоянная Больцмана,
Результаты[править]
При исследовании колебаний энергии в одномерных кристаллах рассматривается два метода осреднения случайных процессов:
1. По пространству: система рассчитывается для большого количества частиц, делится на 𝑛 отрезков по 𝑚 частиц, после чего находится среднее значение для каждого отрезка.
2. По ансамблю реализаций: осреднение производится по определенному количеству реализаций одной и той же системы (По ансамблю можно осреднять потому, что мы считаем один и тот же процесс, основанный на генерации случайных чисел).
Осреднение по пространству проводится следующим образом: 𝑁 частиц делится на 100 отрезков по 𝑁/100 частиц в каждом отрезке. Для каждого отрезка
находится среднее значение, которое и используется для построения графика.
Для каждой системы рассматривается 𝑅 реализаций. Температура усредняется
сначала по реализациям, а только потом по пространству
Рассматривается одномерный кристалл, состоящий из 𝑁 частиц. Исследуются
два случая:
1) В первом случае в начальный момент времени первая половина кристалла нагрета с помощью задания случайных скоростей частиц, вторая половина находится в состоянии покоя
- Число частиц , число реализаций 200
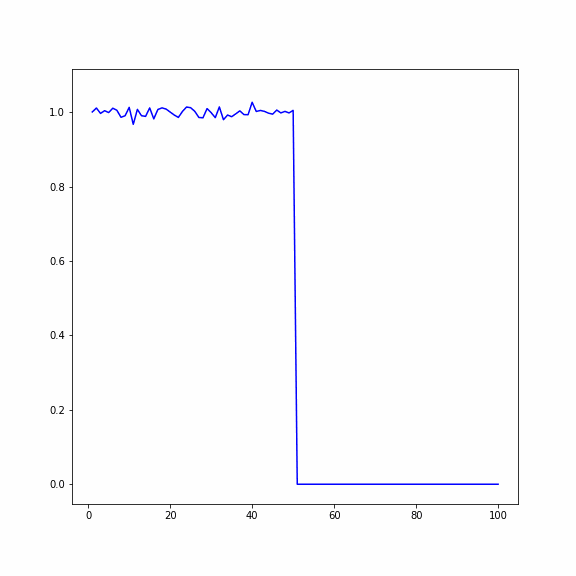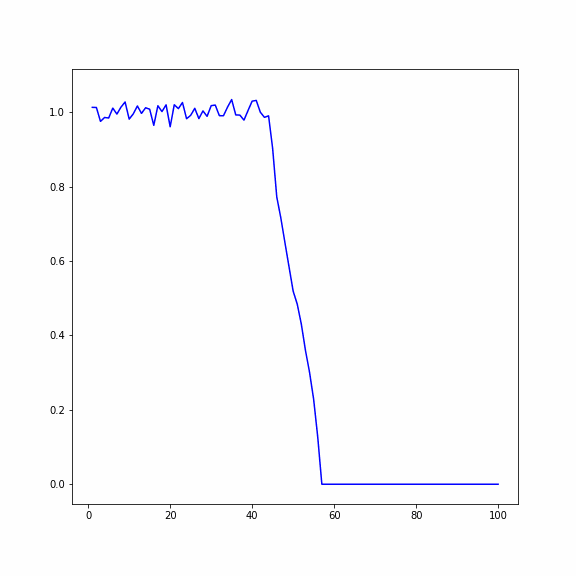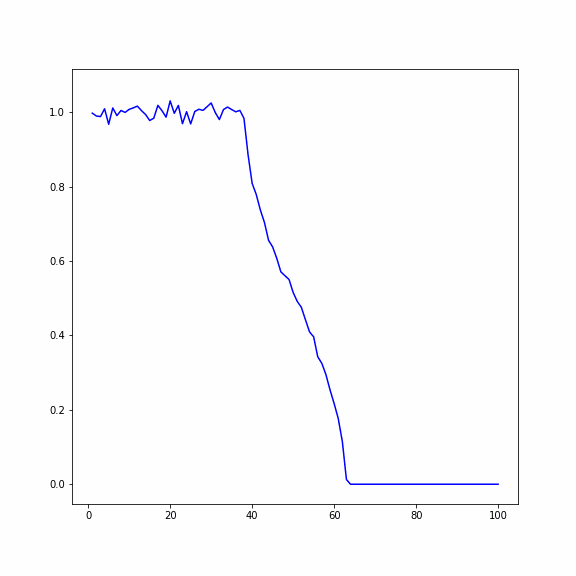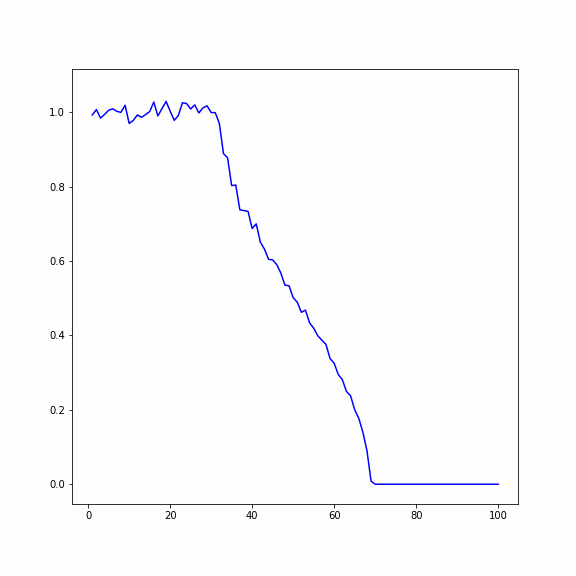
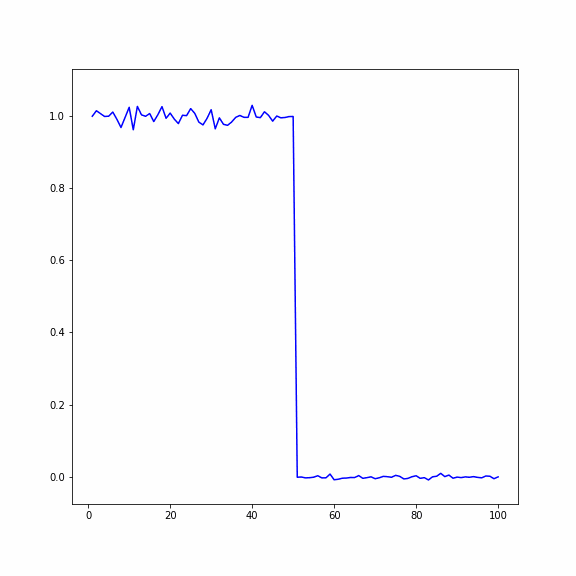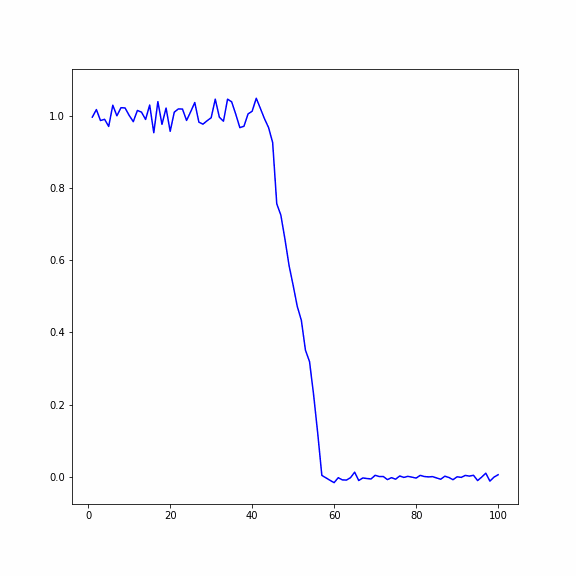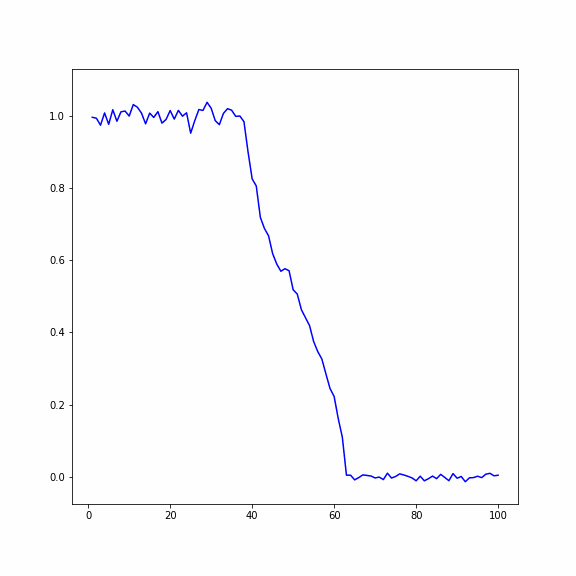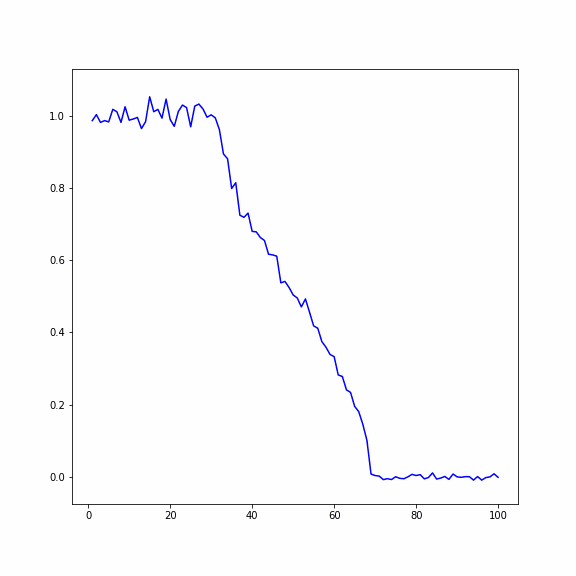
Распространение температуры в кристалле (по горизонтали длина кристалла, вертикали - температура)
2) Во втором случае в начальный момент времени всем частицам заданно случайное перемещение, при этом у первой половины перемещения в два раза больше
- Число частиц , число реализаций 200
Распространение температуры в кристалле (по горизонтали длина кристалла, вертикали - температура)
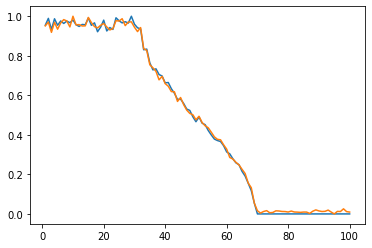
Сравнение двух случаев при числе частиц , число реализаций 200
1 import matplotlib.pyplot as plt
2 import numpy as np
3 import time
4 from numpy import pi
5 %matplotlib inline
6
7 from matplotlib import cm
8 from celluloid import Camera
9 camera = Camera(plt.figure(figsize=(8, 8)))
10
11 start = time.time()
12 Np = 10**4 # mod 100
13 Ns = 12000 # mod 2
14 C = 1
15 m = 1
16
17 w0 = np.sqrt(C/m)
18 dt = (2*pi/w0)/40
19
20 T = np.zeros((int(Ns/2)-1,100))
21 def calculation(random_number):
22 global T
23 np.random.seed(random_number)
24 U = np.zeros((2, Np))
25 V = np.zeros(Np)
26 # first step
27 # V[:(Np)//2] = (np.random.random((Np)//2) * 2 - 1)
28 # U[1,:] = V*dt
29
30 U[1,:Np//2] = (np.random.random(Np//2) * 2 - 1)*2*dt
31 U[1,Np//2:] = (np.random.random(Np//2) * 2 - 1)*dt
32
33 # next steps
34 l = lambda x,y : (x[y-1] - 2*x[y] + x[y+1])
35 for k in range(0,int(Ns/2)-1):
36 U[0,:Np-1] = dt**2 * l( U[1],np.arange(0,Np-1) ) + 2*U[1,:Np-1] - U[0,:Np-1]
37 U[1,:Np-1] = dt**2 * l( U[0],np.arange(0,Np-1) ) + 2*U[0,:Np-1] - U[1,:Np-1]
38 # velosity and temperature:
39
40 V_2 = ((U[1] - U[0])/dt)**2
41 T[k,:] = T[k,:] + np.mean(V_2.reshape(100,int(Np/100)), axis=1)
42
43 Number_of_realization = 200
44 for i in np.random.random(Number_of_realization):
45 calculation(int(i*100))
46
47 x = np.arange(1,101)
48 for k in range(59):
49 y = T[k*100,:]/(Number_of_realization)
50 y = y - np.mean(y[80:])
51 plt.plot(x, y/np.mean(y[:20]), color='blue')
52 camera.snap()
53 anim = camera.animate(blit=True)
54 anim.save('chain2.gif')
55
56 end = time.time()
57 print(end-start)