Вынужденные колебания цепочки в вязкой среде

Курсовой проект по Механике дискретных сред

Исполнитель: Шпетный Даниил

Группа: 3630103/60101

Семестр: осень 2019

Постановка задачи

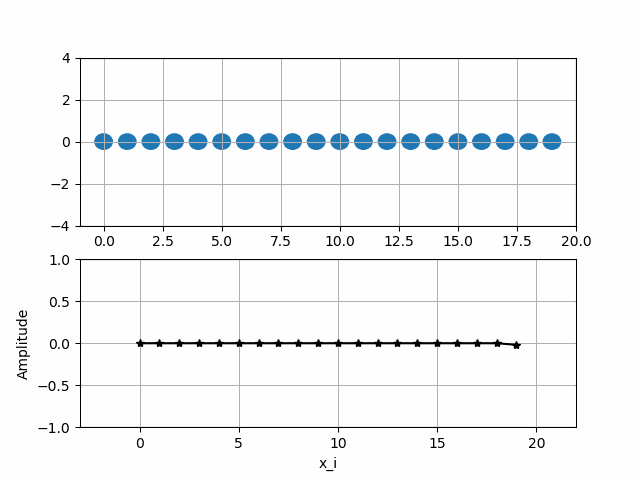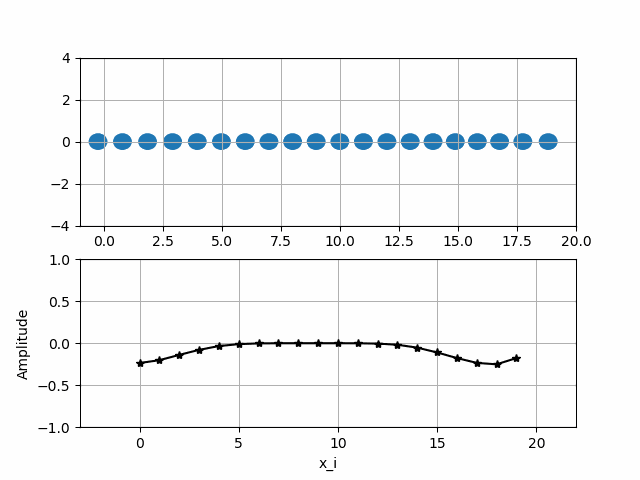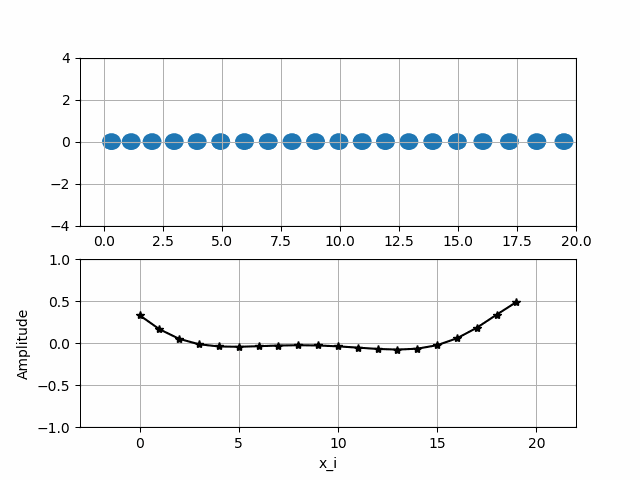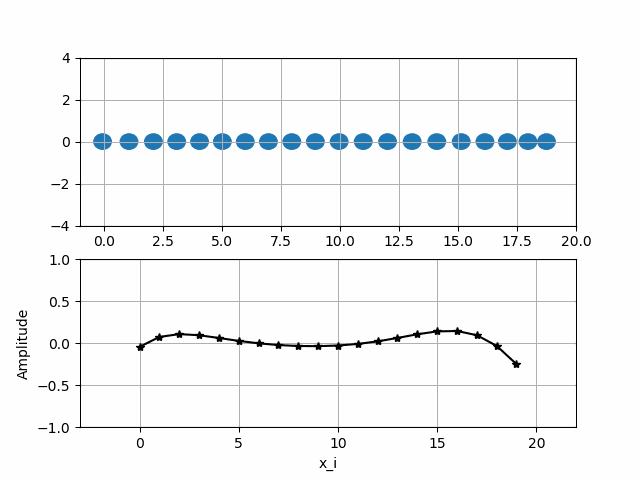
Исследовать вынужденные колебания в вязкой среде. Построить график перемещений частиц от времени.

Построение модели

Процесс моделируется как одномерные колебания цепочки частиц.

Теоретическая сводка

Парное взаимодействие определяется формулой:

[math]F = c(x_{k+1}-x_{k})[/math]

где [math]F[/math] — сила взаимодействия, [math]c[/math] — жесткость связи, [math]x_k[/math] — перемещение частицы, [math]k[/math] — номер частицы.

Уравнение скорости частиц [math]k[/math] и [math]k+1[/math]:

[math]V_{k}=\frac{F}{m}dt-2μV_{k}[/math]

[math]V_{k+1}=-\frac{F}{m}dt-2μV_{k+1}[/math]

где [math]F[/math] — сила взаимодействия, [math]m[/math] — масса частицы, [math]μ[/math] — коэффициент вязкости, [math]V_{k}[/math] — скорость частицы.

Граничные и начальные условия

Начальные условия нулевые

Периодические граничные условия:

[math]V_{N}=c(x_{1}+aN-x_{N}-1)\frac{dt}{m}-2μV_{N}+Qcos(ωt)[/math]

[math]V_{1}=-c(x_{1}+aN-x_{N}-1)\frac{dt}{m}-2μV_{1}[/math]

где [math]Q[/math] — амплитуда возмущающей силы, [math]ω[/math] — частота возмущающей силы, [math]N[/math] — количество частиц.

Визуализация

Текст программы на языке Python (среда разработки PyCharm):

 1 import numpy as np
 2 import math
 3 import matplotlib.pyplot as plt
 4 from matplotlib.patches import Circle
 5 from matplotlib.collections import PatchCollection
 6 from celluloid import Camera
 7 
 8 
 9 def Plotting(X, rad, u):
10     n = np.shape(X)[1]
11     patches = []
12     for it in range(n):
13         circle = Circle((X[0, it], 0), rad)
14         patches.append(circle)
15     p = PatchCollection(patches)
16     ax_1 = plt.subplot(2, 1, 1)
17     plt.plot()
18     ax_1.add_collection(p)
19 
20     plt.xlim([-1, N])
21     plt.ylim([-4, 4])
22     plt.grid(True)
23 
24 
25     ax_2 = plt.subplot(2, 1, 2)
26     plt.plot(np.arange(0, N), u.T, '*-k')
27     plt.xlim([-3, (n + 2) * a])
28     plt.ylim([-1, 1])
29     plt.grid(True)
30     plt.xlabel("x_i")
31     plt.ylabel("Amplitude")
32 
33     plt.pause(0.01)
34     plt.delaxes(ax_1)
35     plt.delaxes(ax_2)
36 
37 
38 
39 #Constants
40 N = 20
41 mu = 0.05
42 c = 1
43 a = 1
44 dt = 0.2
45 m = 1
46 rad = 0.4
47 q = -0.1
48 ST = 1000
49 
50 
51 #Creating arrays
52 X = np.zeros((1, N))
53 U = np.zeros((N, ST))
54 X0 = np.arange(N)
55 X[0, :] = [it*a for it in range(N)]
56 
57 V = np.zeros((1, N))
58 
59 #fig = plt.figure()
60 #fig, axes = plt.subplots(2)
61 #camera = Camera(fig)
62 
63 for st in range(ST):
64     #print(st)
65     for sp in range(0, N-1): #loop for springs
66 
67         F = c*(X[0, sp+1] - X[0, sp] - 1)
68         V[0, sp] += F / m * dt - 2*mu*V[0, sp]
69         V[0, sp+1] += -F / m * dt - 2*mu*V[0, sp+1]
70 
71 #Periodical Boundary cond
72     V[0, N-1] += c * (X[0, 0] + a * N - X[0, N-1] - 1) * dt / m - 2*mu*V[0, N-1] + q*math.cos((st)*2*math.pi/100)
73     V[0, 0] += -c * (X[0, 0] + a * N - X[0, N-1] - 1) * dt / m - 2*mu*V[0, 0]
74 #Positions
75     X[0, :] += V[0, :]*dt
76 
77     Plotting(X, rad, X-X0)
78     #camera.snap()
79     #anim = camera.animate(blit=True)
80     #anim.save('MDS.gif')

См. также

• Метод динамики частиц
• Механика дискретных сред
• Введение в механику дискретных сред
• Виртуальная лаборатория
• Курсовые работы 2012-2013 учебного года
• Курсовые работы 2013-2014 учебного года
• Курсовые работы 2014-2015 учебного года
• Курсовые работы 2016-2017 учебного года