Математическая модель лука

БАКАЛАВРСКАЯ РАБОТА
Автор работы: К.П. Фролова
Руководитель: канд. физ.-мат. наук, доцент О.С. Лобода

Предисловие

Данная работа включает в себя результаты, полученные в курсовом проекте по теоретической механике, а также является продолжением освещенной в нем темы моделирования конструкции лука.

Введение

Лук является одним из первых механических устройств, созданных человеком. В наши дни такое оружие, как лук, все еще остается популярным. Современные спортивные луки используются в соревнованиях, в том числе, в Олимпийских играх. Большим спросом пользуются и классические охотничьи луки.
Б.А. Виноградский в 2004 году проанализировал состояние и перспективы развития стрельбы из лука в мире по результатам XXVIII Олимпийских игр в Афинах. Резюмируя, он отметил, что развитие стрельбы из лука как вида спорта на международной арене можно оценить как стабильное, а также подчеркнул, что отмечается постепенный рост спортивного результата, ужесточение спортивной борьбы и повышение конкуренции.
Краткий экскурс на тему основных понятий и принципов, касающихся темы стрельбы из лука, приведен в курсовом проекте по теоретической механике.

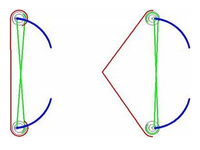
В данной работе обратим внимание на принципиальное различие между классическим и блочным луком. Заключается оно в том, что в блочном луке плечи непосредственно изгибаются не тетивой, а тросами.
При оттягивании тетивы она сматывается с блока большего радиуса и прокручивает его. На блок меньшего радиуса, вращающийся с ним синхронно, в это время наматывается силовой трос, соединенный с противоположным плечом. Таким образом, трос, наматываемый на верхний блок, сгибает нижнее плечо лука, а трос, наматываемый на нижний блок, сгибает верхнее плечо лука.
Если с конструкции снять тросы и при этом оттягивать тетиву, то плечи не согнутся.



И.Ф. Заневский отметил «эволюцию» моделей, созданных рядом ученых. Так, С.Х. Хикман описал лук моделью, в которой плечи являются прямыми и недеформируемыми, между которыми располагаются идеальные шарниры с пружиной Архимеда, а концы которых соединены нерастяжимой тетивой. Б.В. Куи и Дж.А. Спаренберг в своей модели рассмотрели плечо лука в качестве упругой полосы. Среди российских работ в области создания математической модели лука можно подчеркнуть работу А.А. Лужина, который смоделировал плечи лука пластинами Кирхгофа – Лява, тетиву - нерастяжимой нитью, а стрелу – сосредоточенной массой. При этом задача решалась в линейной постановке для малых прогибов плеч. Разработка модели блочного лука представляет наибольший интерес в современном мире. Тем не менее, для того, чтобы перейти к ней, необходимо понимание характера процессов, происходящих в классических луках. Особое внимание уделяется азиатскому луку. Особенностью его конструкции являются негнущиеся концы плеч, называемые «ушами», благодаря которым усилие натяжения лука резко увеличивается в начале и гораздо более плавно - в конце. Модель такого лука описали в своей работе Б.В.Куи и Дж.А. Спаренберг и показали, что конструкция позволяет запасти больше энергии. Математическую модель блочного лука предложил Дж.Л. Парк.

Постановка задачи

Целью является описание механической конструкции лука с помощью математического аппарата. В рамках данной работы внимание уделяется двум моделям. В одном случае плечи лука рассматриваются как абсолютно жесткие стержни, в другом у них имеется характеристика на изгиб.
Необходимо:

• Найти зависимость силы натяжения лука от смещения тетивы, построить динамические кривые
• Найти зависимости энергии, накапливаемой в конструкции, от смещения тетивы
• Найти зависимости начальной скорости стрелы от смещения тетивы
• Провести сравнение полученных результатов с экспериментальными данными

Также в рамках работы нужно продемонстрировать эффективность применения системы эксцентричных блоков в конструкции лука. Для этого

• Разобрать в теории принцип действия конструкции
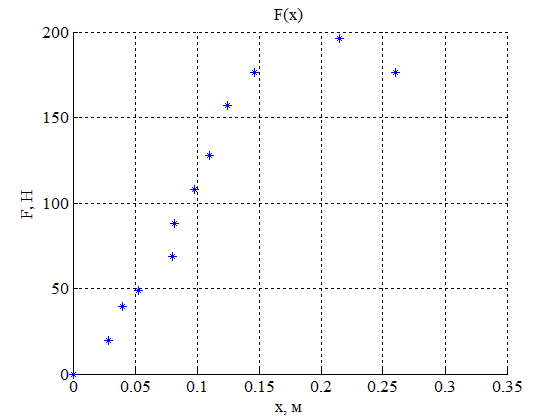
• Построить зависимость усилия натяга от смещения тетивы на основании экспериментальных данных

Модель лука с абсолютно жесткими стержнями

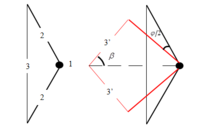
В качестве недеформированного состояния лука принимается состояние, когда плечи представляют собой два прямых стержня, концы которых соединены тетивой, имеющей некое начальное смещение.Между плечами располагается спиральная пружина конечной жесткости, моделируемая телом – точкой (т.е. она занимает нулевой объем, но при этом имеет инерцию на вращение). Плечи лука расположены симметрично относительно оси, проходящей через точку, обозначающую пружину, и середину тетивы.
Имеет место момент, создаваемый посредством пружины, описываемый формулой
[math]M \ =\ c\varphi[/math], где где M – момент пружины, c – жесткость пружины, [math]\varphi[/math] - угол отклонения плеча лука.
Поскольку конструкция лука находится в статическом равновесии в момент, когда тетива оттягивается, сила натяжения тетивы и сила натяжения лука, прикладываемая к середине тетивы, будут описываться формулами:
[math]T = \frac{c\varphi}{h}[/math], где T - сила упругости тетивы, h - плечо силы T.
[math]F \ =\ 2T\cos\beta \ =\ 2\frac{c\varphi}{h}\cos\beta[/math], где F – сила натяжения лука, [math]\beta[/math] – угол, образуемый между оттягиваемой тетивой и плечом лука.
Силу, прикладываемую к луку, необходимо выразить через геометрические параметры конструкции (длину плеча лука и базу (величину начального смещения тетивы)), через величину жесткости спиральной пружины, а также через смещение тетивы.
Оказалось, что [math]F = F( x) \ =\ \frac{\partial F}{\partial x}(0)x+ \frac{1}{2}*\frac{\partial^2F}{\partial x^2}(0)x^2 + \frac{1}{6}*\frac{\partial^3F}{\partial x^3}(0)x^3[/math]
Проведенные расчеты показали, что [math]\frac{\partial F}{\partial 0}(0) \ =\ 0 ;\quad \frac{\partial^2F}{\partial x^2}(0) \ =\ 0[/math]
[math]\frac{\partial^3F}{\partial x^3}(0) \ =\ \frac{12c(l^2 - 2x_0^2)}{l^2x_0^2\sqrt{(l^2 - x_0^2)}} [/math]
Таким образом, [math]F( x) \ =\ \frac{2c(l^2 - 2x_0^2)}{l^2x_0^2(l^2 - x_0^2)}x^3[/math]

Модель лука с упругими стержнями

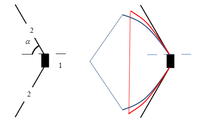
Решается статическая задача в линейной постановке теории стержней. В недеформированном состоянии плечи лука представляют собой прямые стержни, находящиеся под некоторым углом к горизонту. В решаемой задаче плечи лука допустимо моделировать балками Бернулли – Эйлера, т.к. они достаточно хорошо описывают тонкие стержни. В данном случае считается, что внешние моменты отсутствуют, также можно пренебречь инерцией вращения. Кроме того, полагается, что жесткость балки Бернулли – Эйлера на поперечный сдвиг бесконечно велика, но при этом поперечная сила остается ограниченной, что приводит к тому факту, что вектор деформаций сдвига является нулевым. Распределенные нагрузки и моменты отсутствуют.
Уравнения равновесия стержней представлены системой

Эксперименты

• Эксперимент с классическим луком

Эксперимент проводился с прямым симметричным луком. Материал плеч – стеклотекстолит.
Ход выполнения эксперимента заключался в следующем: рукоять лука фиксировалась, затем к середине тетивы крепился груз известной массы, после чего с помощью рулетки измерялось значение смещения тетивы от положения, когда она не деформирована. Таким образом, снималась зависимость массы подвешиваемого груза от смещения тетивы, которая для дальнейших расчетов преобразовывалась в зависимость силы натяжения лука от указанного перемещения.

• Эксперимент с блочным луком

Эксперимент проводился с блочным луком «Ястреб». Лук имеет стандартные эксцентричные блоки, карбоновые плечи и рукоять из алюминий - магниевого сплава.
Ход эксперимента такой же, как и в случае с классическим луком.

Результаты

Для сравнения динамических кривых, построенных для двух моделей, описывающих лук, а также для определения расхождения их с динамической кривой, построенной по экспериментальным данным, учитывалось, что такие параметры лука, как длина плеча, а также начальное смещение тетивы в обеих моделях равны соответствующим параметрам реальной конструкции. Также было принято, что совпадают значения максимальной величины силы натяжения лука.
Величина жесткости спиральной пружины в модели лука с абсолютно жесткими плечами определялась, исходя из соображений о том, что модель должна как можно точнее описывать реальную конструкцию.С этой целью использовался метод наименьших квадратов. Оказалось, что [math] c = 23.169[/math] Нм .
Жесткость лука, описываемого моделью с упругими плечами, выражалась через значения модуля Юнга и момент инерции поперечного сечения плеча лука: [math]c = EI[/math]. При этом для сравнения с экспериментом необходимо принять, что жесткость, используемая в модели, соответствует реальной жесткости плеча лука. Для этого необходимо равенство соответствующих модулей Юнга, а также моментов инерции поперечного сечения плеча лука. Момент инерции определяется следующей формулой:
[math]I \ =\ \frac{bh^3}{12}[/math], где где [math]b[/math] и [math]h[/math] – ширина и высота поперечного сечения соответственно.
В реальной конструкции плечо лука имеет переменную ширину и постоянную высоту сечения. Экспериментально снятые значения зависимости ширины сечения от координаты вдоль плеча аппроксимировались линейной функцией, описываемой следующей формулой: [math]b = 0.0316s + 0.01[/math]. В результате осреднения момента инерции по достаточно большому количеству точек оказалось, что [math] c_1 = 24.852[/math]

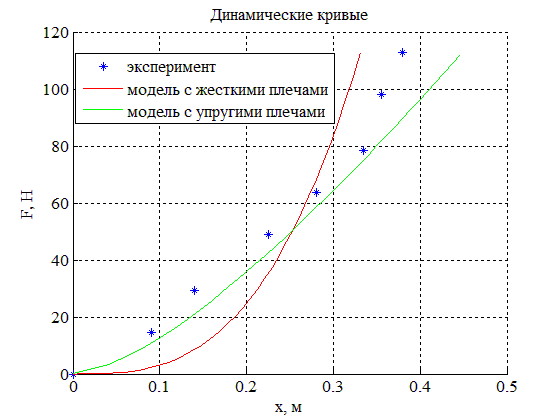
Построены динамические кривые, иллюстрирующие зависимости силы натяжения лука от смещения тетивы для обеих моделей, а также для экспериментальной конструкции.Из графиков видно, что кривая, построенная для модели лука, в котором стержни рассматриваются как балки Бернулли – Эйлера, проходит ближе к экспериментальной, нежели динамическая кривая, характеризующая лук с абсолютно жесткими плечами. Также визуально можно оценить, что площадь под графиком, построенным для модели с упругими плечами, больше, чем площадь под графиком, описывающим другую модель. Следствием этого является тот факт, что работа и, соответственно, мощность лука с упругими плечами превышает соответствующий показатель лука с абсолютно жесткими стержнями.
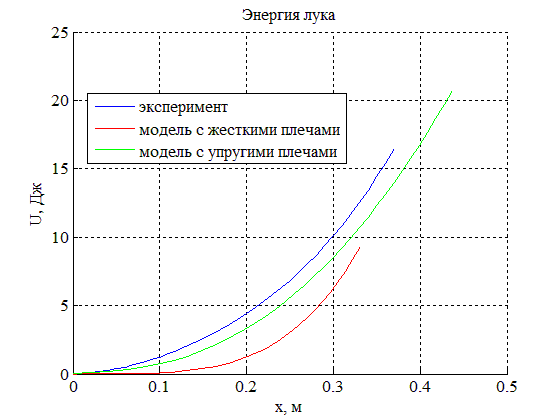
Для качественной и количественной оценки мощностей луков, описываемых обеими моделями, рассматриваемыми в данной работе, построены графики зависимости энергии, накапливаемой в конструкции лука, от величины смещения тетивы. Из графиков видно, что действительно мощность лука с упругими плечами превышает мощность лука с абсолютно жесткими стержнями и точнее описывает данную характеристику при сравнении с экспериментальными данными.
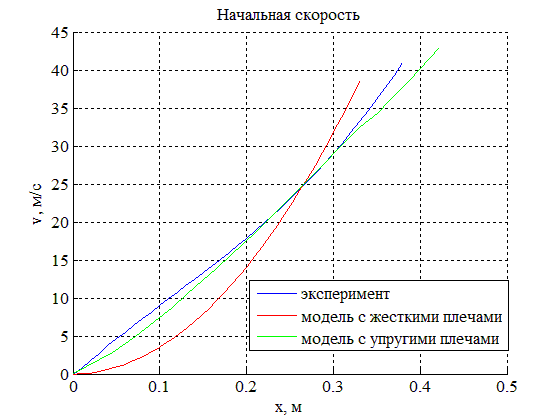
Помимо динамической кривой лука, а также его мощности, интерес представляет такая характеристика конструкции, как начальная скорость, придаваемая стреле. Видно, что зависимость начальной скорости стрелы от смещения тетивы для модели с упругими плечами точнее описывает соответствующую зависимость, построенную по экспериментальным данным, чем в случае модели с абсолютно жесткими плечами.

По экспериментальным данным для исследуемого блочного лука построена зависимость усилия натяжения лука, от смещения тетивы. Видно, что у графика имеется пик в точке, где сила натяжения лука является максимальной и составляет 20 кгс. После прохождения пика усилие, ощущаемое стрелком, падает, но при этом накопленная в деформируемых плечах луках мощность никуда не исчезает.

Заключение

В работе рассмотрены

• Модель лука с абсолютно жесткими плечами и пружиной между ними
• Модель лука с плечами, моделируемыми балками Бернулли – Эйлера, задача решена в линейном приближении
• Принцип работы блочного лука

Оказалось, что

• Мощность лука с абсолютно жесткими плечами меньше мощности лука с упругими плечами
• Модель лука с упругими стержнями описывает реальный лук точнее, а также является эффективнее
• Блоки позволяют удерживать в натяжении более мощные луки

Список использованных источников

• Б.А. Виноградский. Анализ состояния и перспективы развития стрельбы из лука в мире с учетом результатов 28 Олимпийских игр в Афинах // Наука в олимпийском спорте – 2005 - № 2 - с. 60 – 68.
• I.F. Zaniewski. Modeling of the archery bow and arrow vibrations // Shock and Vibration – 2009 - №3 - p. 307 – 317.
• С. Кондратьев. Термины в стрельбе из лука [электронный ресурс] // Стрельба из лука: [сайт] – 2011 – URL: http://www.archery-sila.ru/
• Э. Макьюэн, А. Миллер, А. Бергман. Конструкция и изготовление древних луков. // В мире науки – 1991 - № 8 - с. 38–75.
• В.Н. Казанцев. Пособие для начинающих лучников [электронный ресурс] // Стрельба из лука: [сайт ] – 2009 – URL: http://www.archery-sila.ru/
• И.Ф. Заневский. Компьютерная модель внутренней баллистики стрелы лука // Сборник научных трудов "Вестник НТУ "ХПИ": Информатика и моделирование – 2011 - №36 - c. 78 – 86.
• C.N. Hickman. Dynamics of a bow and arrow // Journal of Applied Physics – 1937 - V. 8 - p. 404-409.
• B.W. Kooi, J.A. Sparenberg. On the static deformation of a bow // Journal of Engineering Mathematics – 1980 - V. 14, № 1 - p. 27-45.
• А.А. Лужин. Моделирование выстрела из лука: дис. на соискание ученой степени к.ф.-м.н. – Москва, 2008 - 103 с.
• T.M. Hamilton. Native American Bow. Columbia: Published by Missouri Archeological Society, 1982 – 148 p.
• J.L. Park. The behaviour of an arrow shot from a compound archery bow // Proc. Of the IMechE, Part P: Journal of Sports Engineering and Technology. – 2011. – V. 225, № 8. – p. 8 - 21.
• П.А. Жилин. Прикладная механика. Теория тонких упругих стержней. СПб.: Изд-во Политехнического университета, 2007 - 101 с.
• J.E. Gordon. Structures, or why Things don't Fall Down. Harmondsworth: Published by the Penguin Books, 1978 – 395 p.