Математическая модель лука — различия между версиями
(→Эксперимент) |
(→Эксперимент и обработка полученных данных) |
||
| Строка 34: | Строка 34: | ||
==Модель лука с абсолютно жесткими стержнями== | ==Модель лука с абсолютно жесткими стержнями== | ||
==Модель лука с упругими стержнями== | ==Модель лука с упругими стержнями== | ||
| − | ==Эксперимент | + | ==Эксперимент== |
* Эксперимент с классическим луком | * Эксперимент с классическим луком | ||
Эксперимент проводился с прямым симметричным луком. Материал плеч – стеклотекстолит<br> | Эксперимент проводился с прямым симметричным луком. Материал плеч – стеклотекстолит<br> | ||
[[Файл:Bow.jpg|200px|thumb|left|]] | [[Файл:Bow.jpg|200px|thumb|left|]] | ||
Ход выполнения эксперимента заключался в следующем: рукоять лука фиксировалась, затем к середине тетивы крепился груз известной массы, после чего с помощью рулетки измерялось значение смещения тетивы от положения, когда она не деформирована. Таким образом, снималась зависимость массы подвешиваемого груза от смещения тетивы, которая для дальнейших расчетов преобразовывалась в зависимость силы натяжения лука от указанного перемещения. <br> | Ход выполнения эксперимента заключался в следующем: рукоять лука фиксировалась, затем к середине тетивы крепился груз известной массы, после чего с помощью рулетки измерялось значение смещения тетивы от положения, когда она не деформирована. Таким образом, снималась зависимость массы подвешиваемого груза от смещения тетивы, которая для дальнейших расчетов преобразовывалась в зависимость силы натяжения лука от указанного перемещения. <br> | ||
| + | ==Результаты== | ||
| + | Для сравнения динамических кривых, построенных для двух моделей, описывающих лук, а также для определения расхождения их с динамической кривой, построенной по экспериментальным данным, учитывалось, что такие параметры лука, как длина плеча, а также начальное смещение тетивы в обеих моделях равны соответствующим параметрам реальной конструкции. Также было принято, что совпадают значения максимальной величины силы натяжения лука. <br> | ||
| + | Величина жесткости спиральной пружины в модели лука с абсолютно жесткими плечами определялась, исходя из соображений о том, что модель должна как можно точнее описывать реальную конструкцию.С этой целью использовался метод наименьших квадратов. Оказалось, что ''с'' = 23.169 Нм. | ||
==Заключение== | ==Заключение== | ||
==Список использованных источников== | ==Список использованных источников== | ||
Версия 00:32, 15 июня 2014
БАКАЛАВРСКАЯ РАБОТА
Автор работы: К.П. Фролова
Руководитель: канд. физ.-мат. наук, доцент О.С. Лобода
Содержание
Предисловие
Данная работа включает в себя результаты, полученные в курсовом проекте по теоретической механике, а также является продолжением освещенной в нем темы моделирования конструкции лука.
Введение
Лук является одним из первых механических устройств, созданных человеком. В наши дни такое оружие, как лук, все еще остается популярным. Современные спортивные луки используются в соревнованиях, в том числе, в Олимпийских играх. Большим спросом пользуются и классические охотничьи луки.
Б.А. Виноградский в 2004 году проанализировал состояние и перспективы развития стрельбы из лука в мире по результатам XXVIII Олимпийских игр в Афинах. Резюмируя, он отметил, что развитие стрельбы из лука как вида спорта на международной арене можно оценить как стабильное, а также подчеркнул, что отмечается постепенный рост спортивного результата, ужесточение спортивной борьбы и повышение конкуренции.
Краткий экскурс на тему основных понятий и принципов, касающихся темы стрельбы из лука, приведен в курсовом проекте по теоретической механике.
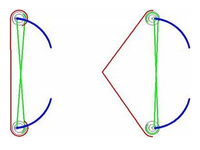
В данной работе обратим внимание на принципиальное различие между классическим и блочным луком. Заключается оно в том, что в блочном луке плечи непосредственно изгибаются не тетивой, а тросами.
При оттягивании тетивы она сматывается с блока большего радиуса и прокручивает его. На блок меньшего радиуса, вращающийся с ним синхронно, в это время наматывается силовой трос, соединенный с противоположным плечом. Таким образом, трос, наматываемый на верхний блок, сгибает нижнее плечо лука, а трос, наматываемый на нижний блок, сгибает верхнее плечо лука.
Если с конструкции снять тросы и при этом оттягивать тетиву, то плечи не согнутся.
И.Ф. Заневский отметил «эволюцию» моделей, созданных рядом ученых. Так, С.Х. Хикман описал лук моделью, в которой плечи являются прямыми и недеформируемыми, между которыми располагаются идеальные шарниры с пружиной Архимеда, а концы которых соединены нерастяжимой тетивой. Б.В. Куи и Дж.А. Спаренберг в своей модели рассмотрели плечо лука в качестве упругой полосы. Среди российских работ в области создания математической модели лука можно подчеркнуть работу А.А. Лужина, который смоделировал плечи лука пластинами Кирхгофа – Лява, тетиву - нерастяжимой нитью, а стрелу – сосредоточенной массой. При этом задача решалась в линейной постановке для малых прогибов плеч. Разработка модели блочного лука представляет наибольший интерес в современном мире. Тем не менее, для того, чтобы перейти к ней, необходимо понимание характера процессов, происходящих в классических луках. Особое внимание уделяется азиатскому луку. Особенностью его конструкции являются негнущиеся концы плеч, называемые «ушами», благодаря которым усилие натяжения лука резко увеличивается в начале и гораздо более плавно - в конце. Модель такого лука описали в своей работе Б.В.Куи и Дж.А. Спаренберг и показали, что конструкция позволяет запасти больше энергии. Математическую модель блочного лука предложил Дж.Л. Парк.
Постановка задачи
Целью является описание механической конструкции лука с помощью математического аппарата. В рамках данной работы внимание уделяется двум моделям. В одном случае плечи лука рассматриваются как абсолютно жесткие стержни, в другом у них имеется характеристика на изгиб.
Необходимо:
- Найти зависимость силы натяжения лука от смещения тетивы, построить динамические кривые
- Найти зависимости энергии, накапливаемой в конструкции, от смещения тетивы
- Найти зависимости начальной скорости стрелы от смещения тетивы
- Провести сравнение полученных результатов с экспериментальными данными
Также в рамках работы нужно продемонстрировать эффективность применения системы эксцентричных блоков в конструкции лука. Для этого
- Разобрать в теории принцип действия конструкции
- Построить зависимость усилия натяга от смещения тетивы на основании экспериментальных данных
Модель лука с абсолютно жесткими стержнями
Модель лука с упругими стержнями
Эксперимент
- Эксперимент с классическим луком
Эксперимент проводился с прямым симметричным луком. Материал плеч – стеклотекстолит
Ход выполнения эксперимента заключался в следующем: рукоять лука фиксировалась, затем к середине тетивы крепился груз известной массы, после чего с помощью рулетки измерялось значение смещения тетивы от положения, когда она не деформирована. Таким образом, снималась зависимость массы подвешиваемого груза от смещения тетивы, которая для дальнейших расчетов преобразовывалась в зависимость силы натяжения лука от указанного перемещения.
Результаты
Для сравнения динамических кривых, построенных для двух моделей, описывающих лук, а также для определения расхождения их с динамической кривой, построенной по экспериментальным данным, учитывалось, что такие параметры лука, как длина плеча, а также начальное смещение тетивы в обеих моделях равны соответствующим параметрам реальной конструкции. Также было принято, что совпадают значения максимальной величины силы натяжения лука.
Величина жесткости спиральной пружины в модели лука с абсолютно жесткими плечами определялась, исходя из соображений о том, что модель должна как можно точнее описывать реальную конструкцию.С этой целью использовался метод наименьших квадратов. Оказалось, что с = 23.169 Нм.