Динамическая потеря устойчивости при кручении — различия между версиями

Текущая версия на 15:09, 25 февраля 2020

Курсовой проект по Механике дискретных сред

Исполнитель: Исаева Сабина

Группа: 3630103/60101

Семестр: осень 2019

Постановка задачи[править]

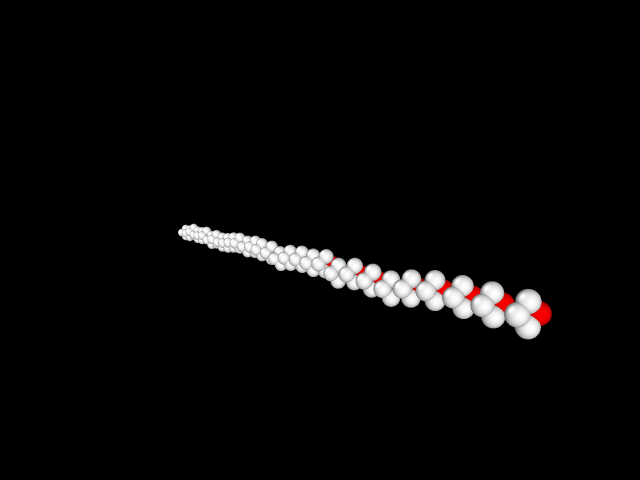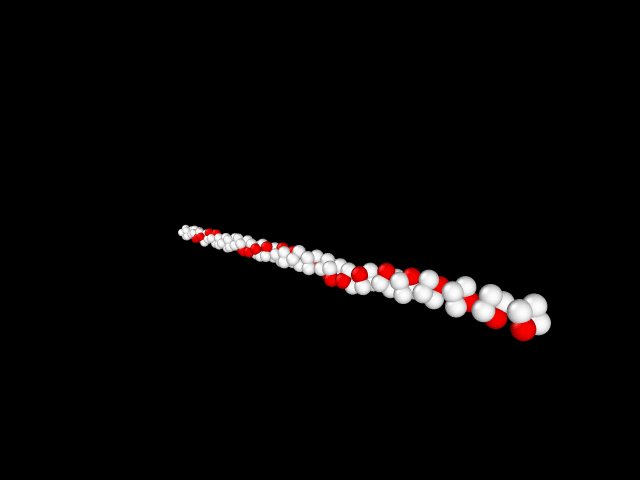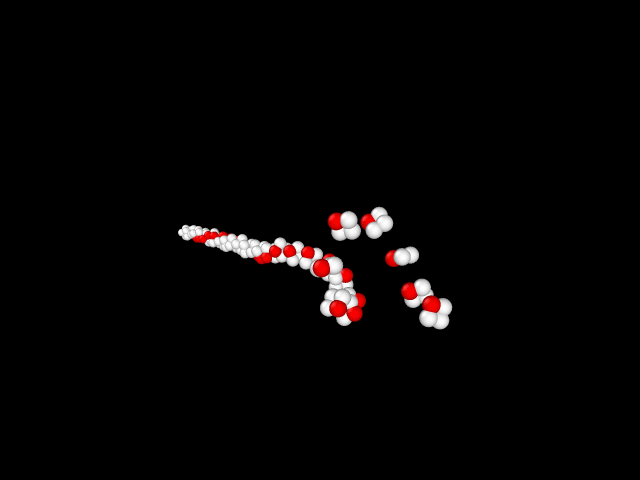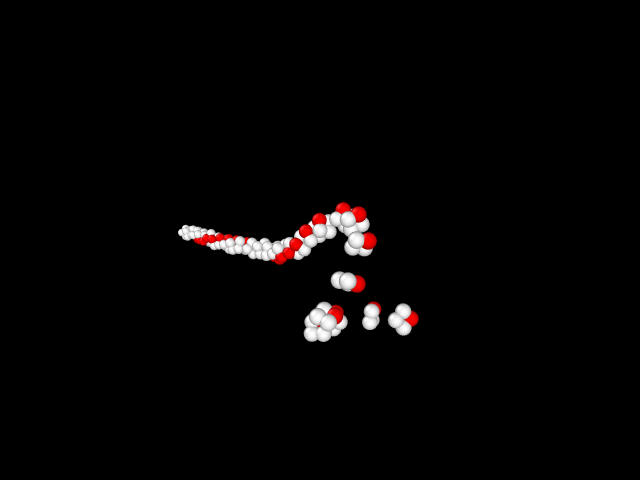
Реализовать динамическую потерю устойчивости при кручении стержня. Один конец стержня жестко закреплен,а другой вращается с угловой скорость ,увеличивающейся со временем.

Построение модели[править]

Материал представлен в виде набора частиц (твердых тел), связанных упругими связями. Граничные условия: Один конец нашей балки жестко зафесирован,другой- вращается

Уравнения сил: [math] F_{ij}=B_{1}(r_{ij}-a)e_{ij}+\frac{B_{2}}{2r_{ij}}(n_{j1}-n_{i1}-e_{ij}\cdot (n_{j1}-n_{i1})e_{ij})) ,[/math]

Уравнение моментов:

[math] M_{ij}=-\frac{B_{2}}{2}e_{ij}\times n_{i1}+M^{TB} ,[/math]
[math] M_{ji}=-\frac{B_{2}}{2}e_{ij}\times n_{j1}+M^{TB} ,[/math]
[math]M^{TB}=B_{3}n_{j1}\times n_{i1}-\frac{B_{4}}{2}(n_{j2}\times n_{i2}+n_{j3}\times n_{i3}),[/math]

где [math]B_{1}=\frac{ES}{a},[/math]
[math]B_{2}=\frac{12EJ}{a},[/math]
[math]B_{3}=\frac{-2EJ}{a}-\frac{GJ_{p}}{2a},[/math]
[math]B_{4}=\frac{GJ_{p}}{a},[/math]
[math] E [/math] - модуль Юнга [math]G [/math]- модуль сдвига [math]a [/math] - общая длина

Результаты[править]

При исследовании вращения нашего тела ,получили неустойчивость.

См. также[править]

• Метод динамики частиц
• Механика дискретных сред
• Введение в механику дискретных сред
• Виртуальная лаборатория
• Курсовые работы 2012-2013 учебного года
• Курсовые работы 2013-2014 учебного года
• Курсовые работы 2014-2015 учебного года
• Курсовые работы 2016-2017 учебного года