Вынужденные колебания цепочки в вязкой среде — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
(→‎Граничные и начальные условия)
Строка 27: Строка 27:
 
где <math>F</math> — сила взаимодействия, <math>m</math> — масса частицы, <math>μ</math> — коэффициент вязкости, <math>V_{k}</math> — скорость частицы.
 
где <math>F</math> — сила взаимодействия, <math>m</math> — масса частицы, <math>μ</math> — коэффициент вязкости, <math>V_{k}</math> — скорость частицы.
  
−
===Граничные и начальные условия===
+
'''Полужирное начертание'''===Граничные и начальные условия===
 
Начальные условия нулевые
 
Начальные условия нулевые
−
:Периодические граничные условия:
+
Периодические граничные условия:
 
:<math>V_{N}=c(x_{1}+aN-x_{N}-1)\frac{dt}{m}-2μV_{N}+Qcos(ωt)</math>
 
:<math>V_{N}=c(x_{1}+aN-x_{N}-1)\frac{dt}{m}-2μV_{N}+Qcos(ωt)</math>
 
:<math>V_{1}=-c(x_{1}+aN-x_{N}-1)\frac{dt}{m}-2μV_{1}</math>
 
:<math>V_{1}=-c(x_{1}+aN-x_{N}-1)\frac{dt}{m}-2μV_{1}</math>

Версия 19:36, 22 января 2020

Курсовой проект по Механике дискретных сред

Исполнитель: Шпетный Даниил

Группа: 3630103/60101

Семестр: осень 2019


Постановка задачи

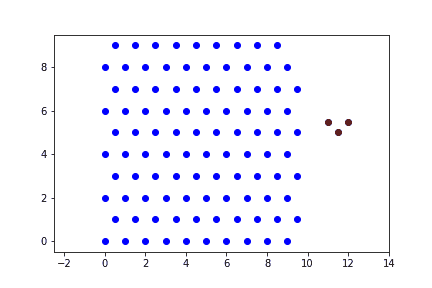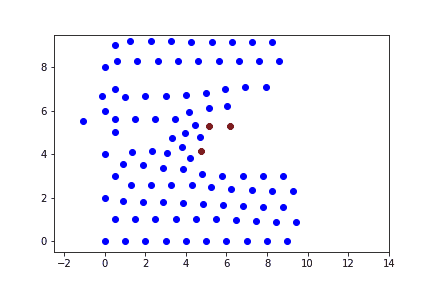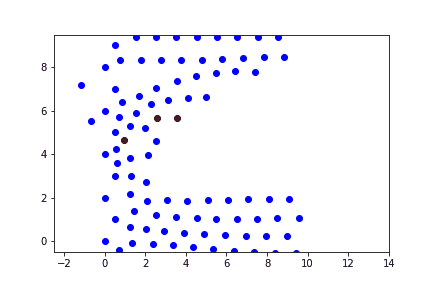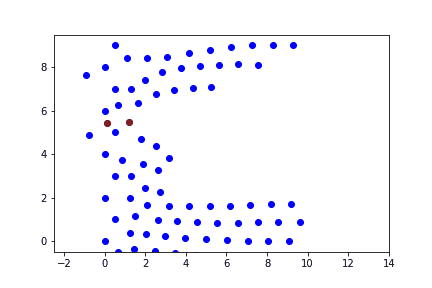
Исследовать вынужденные колебания в вязкой среде. Построить график перемещений частиц от времени.

Построение модели

Процесс моделируется как одномерные колебания цепочки частиц.

Теоретическая сводка

Парное взаимодействие определяется формулой:

[math]F = c(x_{k+1}-x_{k}-1)[/math]

где [math]F[/math] — сила взаимодействия, [math]c[/math] — жесткость связи, [math]x_k[/math] — перемещение частицы, [math]k[/math] — номер частицы.

Уравнение скорости частиц [math]k[/math] и [math]k+1[/math]:

[math]V_{k}=\frac{F}{m}dt-2μV_{k}[/math]
[math]V_{k+1}=-\frac{F}{m}dt-2μV_{k+1}[/math]

где [math]F[/math] — сила взаимодействия, [math]m[/math] — масса частицы, [math]μ[/math] — коэффициент вязкости, [math]V_{k}[/math] — скорость частицы.

Полужирное начертание===Граничные и начальные условия=== Начальные условия нулевые Периодические граничные условия:

[math]V_{N}=c(x_{1}+aN-x_{N}-1)\frac{dt}{m}-2μV_{N}+Qcos(ωt)[/math]
[math]V_{1}=-c(x_{1}+aN-x_{N}-1)\frac{dt}{m}-2μV_{1}[/math]

где [math]Q[/math] — амплитуда возмущающей силы, [math]ω[/math] — частота возмущающей силы, [math]N[/math] — количество частиц.

Решение

При построении модели были приняты следующие значения параметров:

[math]a=1[/math]

[math]D=1[/math]

[math]m=1[/math]

[math]dt=0.001[/math] -шаг по времени

Пуля3.gif

См. также

Источник — «http://tm.spbstu.ru/?title=Вынужденные_колебания_цепочки_в_вязкой_среде&oldid=55000»