Bonded-Particle Model — различия между версиями

Версия 12:18, 1 сентября 2011

Силы и моменты, действующие со стороны связи на частицу

Расчет сил и моментов

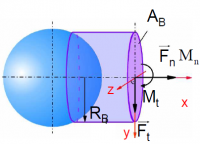
Идея моделирования с использованием Bonded-Particle Model^[1] заключается в инкрементальном изменении сил и моментов, действующих со стороны связи на частицу, согласно следующим уравнениям:

[math]\delta{F_n} = -v_n S_n A_b \delta{t}[/math]

[math]\delta{F_t} = -v_t S_t A_b \delta{t}[/math]

[math]\delta{M_n} = -\omega_n S_t J \delta{t}[/math]

[math]\delta{M_t} = -\omega_t S_n \frac{J}{2} \delta{t}[/math]

, где [math]\delta{F_{n,t}}[/math] - приращение за шаг интегрирования нормальной и тангенциальной составляющей силы, действующей со стороны связи, [math]\delta{M_{n,t}}[/math] - приращение за шаг интегрирования нормальной и тангенциальной составляющей момента, действующего со стороны связи, [math]A_b = \pi {R^2}_b[/math] - площадь поперечного сечения связи, [math]J = \frac{1}{2}\pi {R_b}^4[/math] - полярный момент инерции сечения связи, [math]R_b[/math] - радиус связи, [math]v_{n,t}[/math] - нормальная и тангенциальная проекция относительной поступательной скорости частиц соответственно, [math]\omega_{n,t}[/math] - нормальная и тангенциальная проекция относительной угловой скорости частиц соответственно, [math]S_{n,t}[/math] - нормальная и сдвиговая жесткость связи соответственно, [math]\delta t[/math] - шаг интегрирования. Как правило, при моделировании к представленным выше силам и моментам добавляются силы взаимодействия Hertz-Mindlin'a, которые возникают только при физическом контакте частиц.

Достоинства

1. Параметры модели имеют ясный физический смысл

Недостатки

1. Интеграл вектора угловой скорости не равен углу поворота; конечные повороты не обладают свойством коммутативности. Следовательно момент со стороны связи на частицу аналогичен линейная торсионной пружине только в случае бесконечномалых шагов интегрирования. С поступательным движением таких проблем нет и можно показать, что суммарная сила [math]F[/math] со стороны связи на частицу равна [math]\vec{F} = - k ( \vec{r} - \vec{r_0} )[/math], где [math]k[/math] - жесткость линейной пружины, [math]\vec{r_0}[/math] - вектор, соединяющий частицы в момент создания связи, [math]\vec{r}[/math] - вектор, соединяющий частицы в данный момент времени.
2. В данной модели сложно (если вообще возможно) использовать нелинейный закон межчастичного взаимодействия.
3. Взаимодействие не потенциально

Ссылки

1. ↑ Potyondy D. O. and Cundall P. A, A bonded-particle model for rock. International Journal of Rock Mechanics and Mining Sciences, 41, (2004), pp. 1329-1364 pdf