The mechanics of the Cosserat media
Introduction[править]
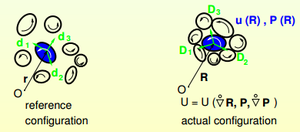
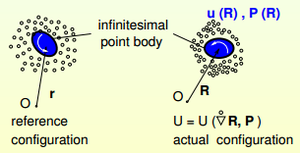
Cosserat medium is a continuum whose point bodies (particles) have rotational degrees of freedom. Examples of Cosserat media: heterogeneous materials with granular structure, composites under loading that causes rotation of (sufficiently rigid) grains (superplastic materials, acoustic metamaterials). Cosserat medium is a particular case of complex medium. Its point-body is rigid. There are other more complex media, e.g. where a point-body is deformable (protein chains, porous media, etc.) It is only a first step to the world of enriched continua. Theory is based on the fundamental laws of mechanics (balance of forces, couples, energy) and, for inelastic media, 2nd law of the thermodynamics, symmetry considerations and material frame indifference. Another branch is the microstructural approach. Experimental methods: under development. We need experiments to determine the moduli. Most of them are based on the experiments on waves (mechanics of magnetic and piezoelectric materials, mechanics of granular materials, rotational seismology...). Reduced Cosserat medium: Cosserat medium that does not react to the gradient of rotation.
Principle of material frame indifference[править]
If a piece of material performs a rigid motion, its stresses rotate together with it and do not depend on the translation. It does not matter if the system of reference is inertial or not. In other words, if the observer moves or rotates, the material does not change its physical behaviour. Mathematically: if in the material there exist stresses and it performs the motion , where do not depend on R, the stresses in this motion will be equal to (stresses are materially objective, frame indifferent).
Basic equations[править]
Stress tensors
If is a force acting upon a unit surface with normal n from the outer part of the volume, there exist a stress tensor (of forces) τ such that . is called Cauchy stress tensor. To prove it Cauchy considered a small tetrahedron and wrote the balance of forces. works on ∇v (gradient of the translational velocity in the actual configuration, v = u˙), and on ω (angular velocity).
If is a couple (torque) acting upon a unit surface with normal n, there exist a tensor µ such that . is called couple stress tensor. works on ∇ω (gradient of the angular velocity in the actual configuration).
Strain tensors in the Cosserat medium
Cosserat deformation tensor:
Transposed wryness tensor:
"Energetic tensors"
Balance of forces: 1st law of dynamics by Euler
()˙ is a material derivative with respect to time (we follow the same point bodies), F is the density of external volumetric force, , R position vector of the centre of mass of a point body, the force acting upon a unit surface S with vector of normal n (from the part of other point bodies outside of the volume V).
Balance of couples: 2nd law of dynamics by Euler
The density of kinetic moment , L is the density of the external volumetric couple, ω is the angular velocity of the point body , I is the tensor of inertia of the point body, the couple acting upon a unit surface S with vector of normal n (from the part of other point bodies outside of the volume V).
Balance of energy
The first law of dynamics by Euler. Local form
2nd law of dynamics by Euler. Local form.
, where
Balance of energy. Local form.
Balance of energy. Local form with “energetic tensors”.
Consider a hyperelastic medium: elastic energy is a funtion of strain tensors. If U = U(A, K), we obtain
These equations are called “constitutive equations”: it is the relation between internal forces/torques and deformations in the medium. They do not depend on nothing external.