Мещерский 48.26 — различия между версиями
(Новая страница: «'''Задача 48.26 из сборника задач Мещерского:''' С помощью языка программирования JavaScript смод…») |
|||
| (не показаны 23 промежуточные версии 5 участников) | |||
| Строка 1: | Строка 1: | ||
'''Задача 48.26 из сборника задач Мещерского:''' С помощью языка программирования JavaScript смоделировать систему блоков с грузом. | '''Задача 48.26 из сборника задач Мещерского:''' С помощью языка программирования JavaScript смоделировать систему блоков с грузом. | ||
| − | + | [[File:48.26.png|thumb|right]] | |
==Формулировка задачи== | ==Формулировка задачи== | ||
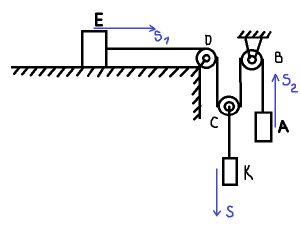
| − | Однородная нить, к концу которой привязан груз А массы m, огибает неподвижный блок В, охватывает подвижный блок С, поднимается вверх на неподвижный блок D и проходит параллельно горизонтальной плоскости, где к ее концу привязан груз Е массы m. К оси блока С прикреплен прикреплен груз К массы <math>{ | + | Однородная нить, к концу которой привязан груз А массы m, огибает неподвижный блок В, охватывает подвижный блок С, поднимается вверх на неподвижный блок D и проходит параллельно горизонтальной плоскости, где к ее концу привязан груз Е массы m. К оси блока С прикреплен прикреплен груз К массы <math>{m_1}</math>. Коэффициент трения скольжения груза Е о горизонтальную плоскость равен f. При каком условии груз К будет опускаться вниз, если начальные скорости всех грузов равнялись нулю? Найти ускорение груза К. Массами блоков и нити пренебречь. |
==Решение задачи== | ==Решение задачи== | ||
Используем уравнение Лагранжа 2-го рода: | Используем уравнение Лагранжа 2-го рода: | ||
| − | <math>\frac{d}{dt}\left(\frac{\partial T}{\partial\dot S_i}\right) - \frac{\partial T}{\partial S_i} = | + | <math>\frac{d}{dt}\left(\frac{\partial T}{\partial\dot S_i}\right) - \frac{\partial T}{\partial S_i} = Q_i , (i = 1,2)</math> , где |
T - кинетическая энергия системы | T - кинетическая энергия системы | ||
Q - обобщенные силы | Q - обобщенные силы | ||
S - независимые обобщенные координаты | S - независимые обобщенные координаты | ||
| − | В данной задаче в качестве обобщенных координат примем расстояния <math>{\partial S_1}</math> | + | В данной задаче в качестве обобщенных координат примем расстояния <math>S_1</math> и <math>S_2</math>. |
| + | : | ||
| + | С учётом выбранных направлений перемещений: <math>S = \frac{S_1 + S_2}{2}</math>. Следовательно, <math>{\dot S} = \frac{\dot S_1 + \dot S_2}{2}; \Delta S = \frac{\Delta S_1 + \Delta S_2}{2}</math> | ||
| + | : | ||
| + | Кинетическая энергия всей системы: | ||
| + | : | ||
| + | <math>T = \frac{1}{2}m\dot S_1^{2} + \frac{1}{2}m_1\dot S^{2} + \frac{1}{2}m\dot S_2^{2} = \frac{1}{2}(m(\dot S_1^{2} + \dot S_2^{2}) + \frac{m_1}{4}(\dot S_1 + \dot S_2)^{2})</math>. | ||
| + | |||
| + | Вычислим частные производные: | ||
| + | : | ||
| + | <math>\frac{\partial T}{\partial\dot S_1} = m\dot S_1 + \frac{m_1}{4}(\dot S_1 + \dot S_2); | ||
| + | \frac{d}{dt}\left(\frac{\partial T}{\partial\dot S_1}\right) = (m + \frac{m_1}{4})\ddot S_1 + \frac{m_1}{4}\ddot S_2; | ||
| + | \frac{\partial T}{\partial S_1} = 0;</math> | ||
| + | : | ||
| + | <math>\frac{\partial T}{\partial\dot S_2} = m\dot S_2 + \frac{m_1}{4}(\dot S_1 + \dot S_2);</math> | ||
| + | <math>\frac{d}{dt}\left(\frac{\partial T}{\partial\dot S_2}\right) = (m + \frac{m_1}{4})\ddot S_2 + \frac{m_1}{4}\ddot S_1;</math> | ||
| + | <math>\frac{\partial T}{\partial S_1} = 0;</math> | ||
| + | : | ||
| + | Найдем сумму работ, действующих на систему: | ||
| + | : | ||
| + | <math>A = m_1g *\Delta S - mg*\Delta S_2 - F_т*\Delta S_1 = g(-fm\Delta S_1 - m\Delta S_2 + m_1\frac{\Delta S_1 + \Delta S_2}{2}) = g((\frac{m_1}{2} - fm)\Delta S_1) + (\frac{m_1}{2}-m)\Delta S_2</math> | ||
| + | : | ||
| + | Отсюда находим обобщённые силы: | ||
| + | : | ||
| + | <math>Q_1 = g(\frac{m_1}{2} - fm)\Delta S_1;</math> | ||
| + | : | ||
| + | <math>Q_2 = g(\frac{m_1}{2}-m)\Delta S_2.</math> | ||
| + | : | ||
| + | Подставляем найденные величины в уравнения Лагранжа: | ||
| + | : | ||
| + | <math>\frac{d}{dt}\left(\frac{\partial T}{\partial\dot S_1}\right) = (m + \frac{m_1}{4})\ddot S_1 + \frac{m_1}{4}\ddot S_2 = g(\frac{m_1}{2} - fm)\Delta S_1</math> | ||
| + | <math> \frac{d}{dt}\left(\frac{\partial T}{\partial\dot S_2}\right) = (m + \frac{m_1}{4})\ddot S_2 + \frac{m_1}{4}\ddot S_1 = g(\frac{m_1}{2}-m)\Delta S_2</math> | ||
| + | : | ||
| + | Сложим уравнения: | ||
| + | : | ||
| + | <math>(m + \frac{m_1}{2})\ddot S_1 + (m + \frac{m_1}{2})\ddot S_2 = g(m_1 - fm - m).</math> | ||
| + | : | ||
| + | И так как <math>{\ddot S} = \frac{\ddot S_1 + \ddot S_2}{2}</math>, то <math>\ddot S = \frac{1}{2}*\frac{g(m_1 - m(1+f)}{m + \frac{m_1}{2}} = g\frac{m_1 - m(1+f)}{2m + m_1}.</math> Это ускорение груза К. Чтобы он опускался вниз, ускорение должно быть отрицательным или <math>m_1 > m(1+f)</math> | ||
| − | + | == Решение == | |
| − | + | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Dementjeva/48.26.html |width=800 |height=600 |border=0 }} | |
| − | |||
Текущая версия на 23:20, 24 декабря 2017
Задача 48.26 из сборника задач Мещерского: С помощью языка программирования JavaScript смоделировать систему блоков с грузом.
Формулировка задачи[править]
Однородная нить, к концу которой привязан груз А массы m, огибает неподвижный блок В, охватывает подвижный блок С, поднимается вверх на неподвижный блок D и проходит параллельно горизонтальной плоскости, где к ее концу привязан груз Е массы m. К оси блока С прикреплен прикреплен груз К массы . Коэффициент трения скольжения груза Е о горизонтальную плоскость равен f. При каком условии груз К будет опускаться вниз, если начальные скорости всех грузов равнялись нулю? Найти ускорение груза К. Массами блоков и нити пренебречь.
Решение задачи[править]
Используем уравнение Лагранжа 2-го рода:
, где
T - кинетическая энергия системы Q - обобщенные силы S - независимые обобщенные координаты
В данной задаче в качестве обобщенных координат примем расстояния и .
С учётом выбранных направлений перемещений: . Следовательно,
Кинетическая энергия всей системы:
.
Вычислим частные производные:
Найдем сумму работ, действующих на систему:
Отсюда находим обобщённые силы:
Подставляем найденные величины в уравнения Лагранжа:
Сложим уравнения:
И так как , то Это ускорение груза К. Чтобы он опускался вниз, ускорение должно быть отрицательным или
Решение[править]