Курсовой проект по Механике дискретных сред
Исполнитель: Вараев Владислав
Группа: 3630103/60101
Семестр: осень 2019
Краткое описание V - model
Тело представляется набором частиц, связанных упругими связями.
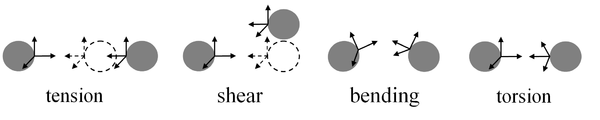
Для двух частиц возможно записать потенциал связи, параметры которого будут связаны с коэффициентами жёсткости связи, соответствующими жёсткостям на продольное растяжение, сдвиг, изгиб и кручение.
Модель описывается следующими формулами:
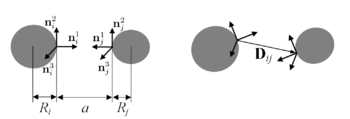
Взаимодействие двух частиц
Сила взаимодействия:
[math]\mathbf{F_{ij}} = B_1 ( D_{ij} - a) \mathbf{d_{ij}} + \frac{B_2}{2D_{ij}}(\mathbf{n_{j1}} - \mathbf{n_{i1}})\cdot(\mathbf{E}-\mathbf{d_{ij}}\mathbf{d_{ij}}) [/math]
Моменты:
[math]\mathbf{M_{ij}} = R_i \mathbf{n_{i1}} \times \mathbf{F_{ij}} - \frac{B_2}{2}\mathbf{d_{ij}}\times \mathbf{n_{i1}}+\mathbf{M_{tb}} [/math]
[math]\mathbf{M_{ji}} = R_i \mathbf{n_{j1}} \times \mathbf{F_{ji}} + \frac{B_2}{2}\mathbf{d_{ij}}\times \mathbf{n_{j1}}-\mathbf{M_{tb}} [/math]
[math]\mathbf{M_{tb}} = B_3 \mathbf{n_{j1}} \times \mathbf{n_{i1}} - \frac{B_4}{2}(\mathbf{n_{j2}}\times \mathbf{n_{i2}}+\mathbf{n_{j3}}\times \mathbf{n_{i3}}) [/math]
Где [math]B_1[/math], [math]B_2[/math], [math]B_3[/math] и [math]B_4[/math] - различные коэффициенты, которые являются характеристиками системы.
Для случая изотропии сдвиговой и изгибной жёсткостей соотношения между жёсткостями системы и коэффициентами имеют следующий вид:
- Жесткость на растяжение-сжатие: [math]c_a = B_1 [/math]
- Жесткость на сдвиг: [math]c_d = \frac{B_2}{a^2} [/math]
- Жесткость на изгиб: [math]c_b = \frac{B_2}{4} + B_3 +\frac{B_4}{2} [/math]
- Жесткость на кручение: [math]c_t = B_4 [/math]
Обобщение на анизотропный случай
Анизотропией будет являться случай, в котором виды сдвиговых и изгибных жёсткостей будут зависеть от осей, относительно которых проводился соответствующий эксперимент. То есть эти жёсткости будут зависеть от разных коэффициентов [math]B[/math].
Тогда предположим следующий вид потенциала:
[math]U = \frac{B_1}{2}(D_{ij} - a)^2 + \frac{B_2}{2}(\mathbf{n_{j1}} - \mathbf{n_{i1}})\cdot\mathbf{d_{ij}} + B_3 \mathbf{n_{i1}}\cdot\mathbf{n_{j1}} - \frac{B_4}{2}(\mathbf{n_{i2}}\cdot\mathbf{n_{j2}} + \mathbf{n_{i3}}\cdot\mathbf{n_{j3}}) + [/math]
С учётом [math] \frac{d\mathbf{d_{ij}}}{d\mathbf{r_{ij}}} = \frac{1}{D_{ij}}(\mathbf{E}-\mathbf{d_{ij}}\mathbf{d_{ij}})[/math] имеем:
[math]\mathbf{F_{ij}} = B_1 ( D_{ij} - a) \mathbf{d_{ij}} + \frac{B_2}{2D_{ij}}(\mathbf{n_{j1}} - \mathbf{n_{i1}})\cdot(\mathbf{E}-\mathbf{d_{ij}}\mathbf{d_{ij}}) + [/math]
[math]\mathbf{M_{ij}} = R_i \mathbf{n_{i1}} \times \mathbf{F_{ij}} - \frac{B_2}{2}\mathbf{d_{ij}}\times \mathbf{n_{i1}}+\mathbf{M_{tb}} + [/math]
Теперь при осуществлении сдвига вдоль оси [math] \mathbf{k} [/math] получаем следующее значение сдвиговой жёсткости:
[math]c_{dk} = \frac{B_2}{a^2} + B_{21}(...)[/math]
а при сдвиге вдоль оси [math] \mathbf{j} [/math]:
[math]c_{dj} = \frac{B_2}{a^2} + B_{22}(...)[/math]
А при изгибе относительно [math] \mathbf{n_{i2} = n_{j2}} [/math] и [math] \mathbf{n_{i3} = n_{j3}} [/math] получаем соответственно:
[math]c_{b2} = \frac{B_2}{4} + B_3 +\frac{B_4}{2} + B_{21}(...)[/math]
[math]c_{b3} = \frac{B_2}{4} + B_3 +\frac{B_4}{2} + B_{22}(...)[/math]
Ссылки