"Распространение тепла в кристалле со случайными перемещениями и нулевыми скоростями"

Курсовой проект по Механике дискретных сред

Исполнитель: Полинов Михаил

Группа: 3630103/60101

Семестр: осень 2019

Постановка задачи

1) Реализовать распространение тепла в одномерном кристалле со случайными перемещениями и нулевыми скоростями в начальный момент времени

2) Сравнить с распространением тепла в одномерном кристалле со случайными скоростями и нулевыми перемещениями в начальный момент времени

Построение модели

Рассмотрим одномерный кристалл: цепочку одинаковых частиц массы m, соединенных одинаковыми линейными пружинами с жесткостью C.

Уравнения динамики кристалла имеют вид:

[math] \ddot u_n = \omega_0^2 (u_{n-1} - 2u_n + u_{n+1}),\quad \omega_0 = \sqrt{\frac{C}{m}} ,[/math]

где [math] u_n [/math] - перемещение [math]n[/math]-й частицы; [math]n[/math] - индекс, принимающий произвольные целые значения, [math]C[/math] - жесткость связи между частицами, [math]m[/math] - масса частицы.

Кинетическая температура T определяется как: [math] T(x)= \frac{m}{k_{b}}\lt \ddot u_i^{2}\gt [/math]
, где [math]k_{b}[/math] — постоянная Больцмана,

Результаты

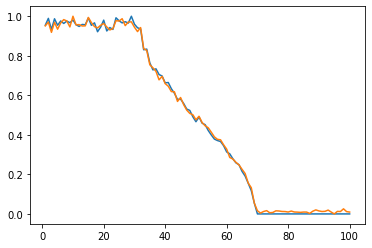
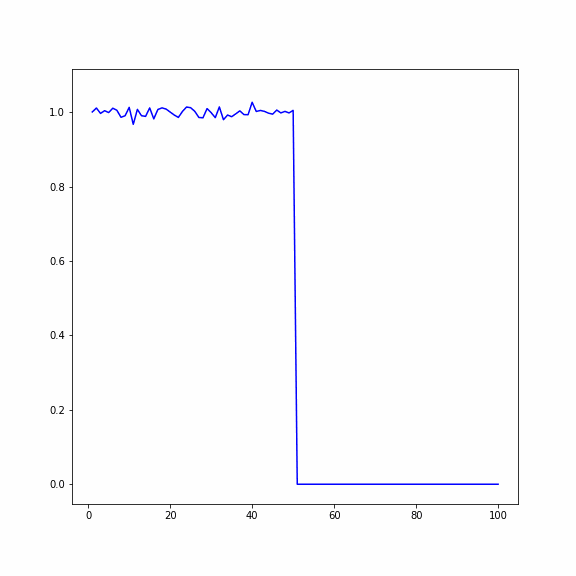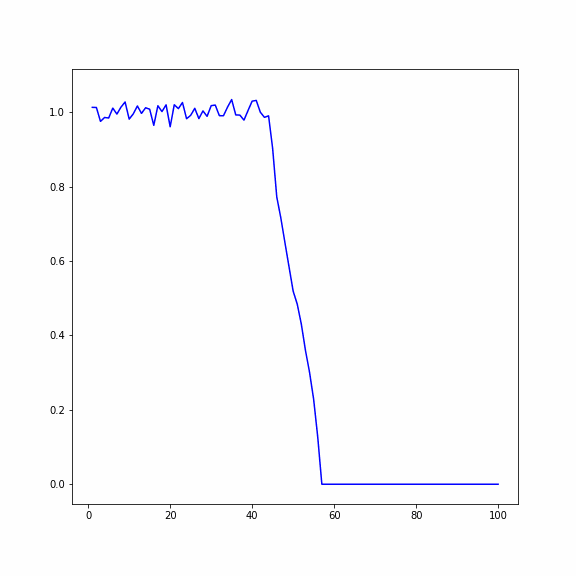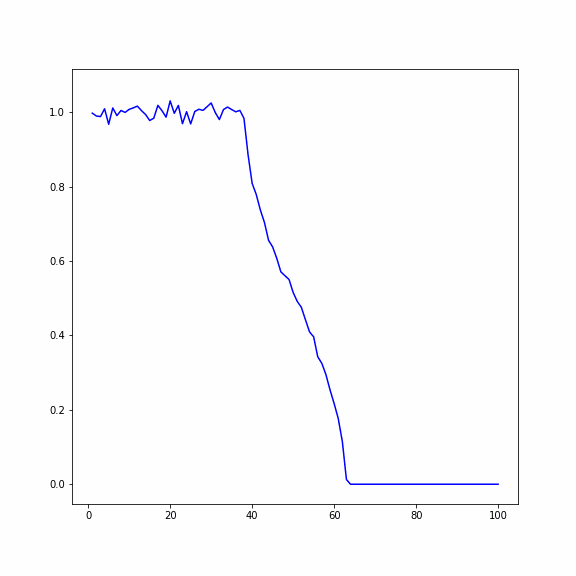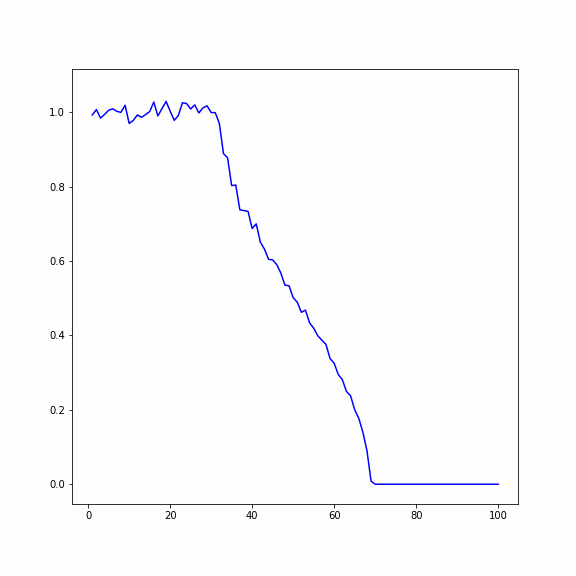
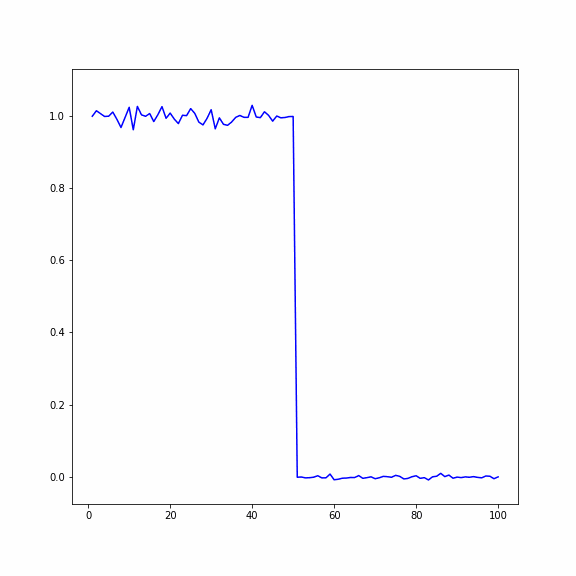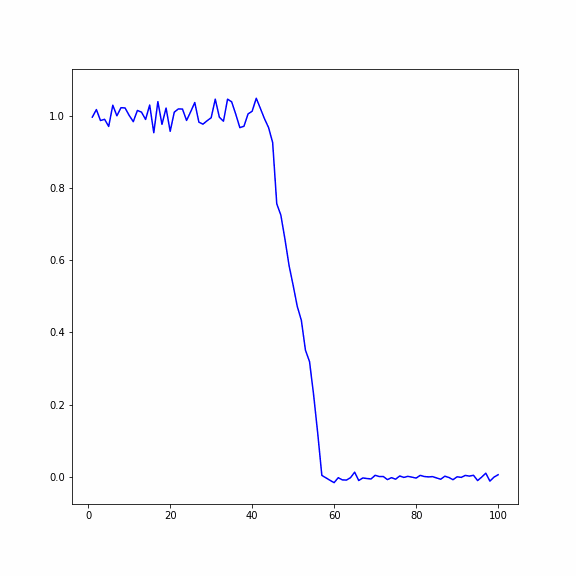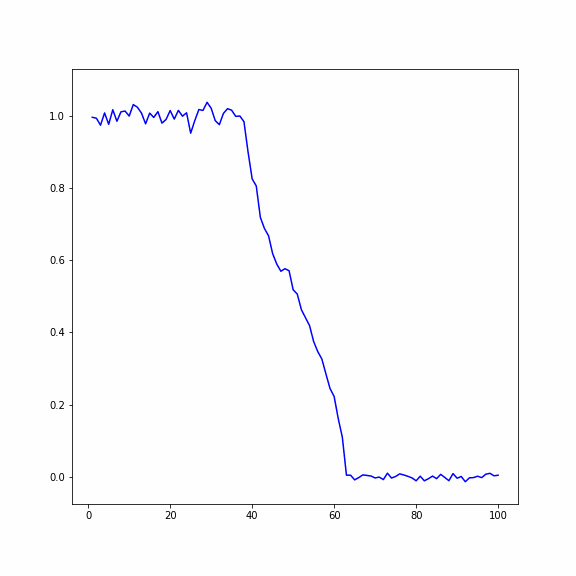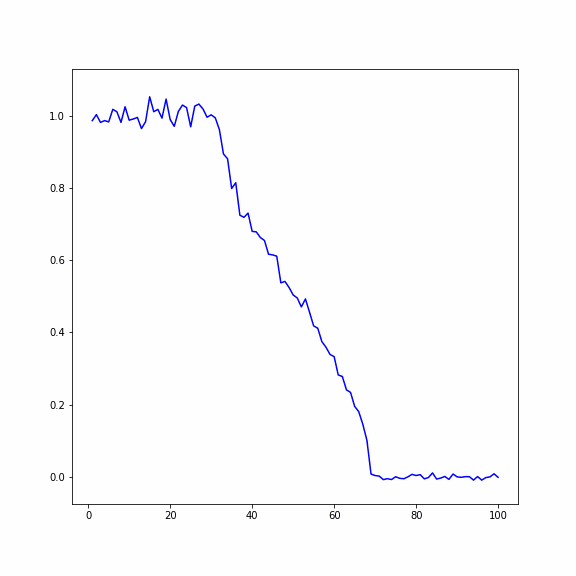
При исследовании колебаний энергии в одномерных кристаллах рассматривается два метода осреднения случайных процессов:

1. По пространству: система рассчитывается для большого количества частиц, делится на 𝑛 отрезков по 𝑚 частиц, после чего находится среднее значение для каждого отрезка.

2. По ансамблю реализаций: осреднение производится по определенному количеству реализаций одной и той же системы (По ансамблю можно осреднять потому, что мы считаем один и тот же процесс, основанный на генерации случайных чисел).

Рассматривается одномерный кристалл, состоящий из 𝑁 частиц. Исследуются два случая:

1) В первом случае в начальный момент времени первая половина кристалла нагрета с помощью задания случайных скоростей частиц, вторая половина находится в состоянии покоя

2) Во втором случае в начальный момент времени всем частицам заданно случайное перемещение, при этом у первой половины перемещения в два раза больше