Обобщение V-model на случай анизотропных сдвиговой и изгибной жёсткостей
Материал из Department of Theoretical and Applied Mechanics
Версия от 13:15, 23 января 2020; Flyingcookie (обсуждение | вклад) (Новая страница: «'''''Курсовой проект по Механике дискретных сред''''' '''Исполни…»)
Курсовой проект по Механике дискретных сред
Исполнитель: Вараев Владислав
Группа: 3630103/60101
Семестр: осень 2019
Краткое описание V - model
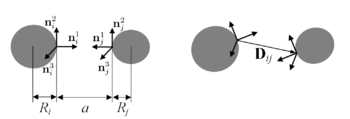
Тело представляется набором частиц, связанных упругими связями Для двух частиц возможно записать потенциал связи, параметры которого будут связаны с коэффициентами жёсткости связи, соответствующими жёсткостям на продольное растяжение, сдвиг, изгиб и кручение
Модель описывается следующими формулами:
Сила взаимодействия:
Моменты:
Где , , и - различные коэффициенты, которые являются характеристиками системы.