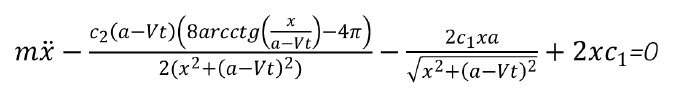Моделирование динамической потери устойчивости стержня при сжатии с постоянной скоростью
Материал из Department of Theoretical and Applied Mechanics
Курсовые работы 2018-2019 учебного года > Моделирование динамической потери устойчивости стержня при сжатии с постоянной скоростью
Курсовой проект по Механике дискретных сред
Исполнитель: Лосева Татьяна
Группа: 43604/1
Семестр: осень 2018
Содержание
Постановка задачи
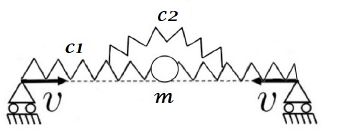
Рассматривалась простая одномерная модель, которая отражает основные физические характеристики стержня, подвергающегося сжатию с постоянной скоростью. Стержень моделируется с помощью частицы, двух линейных пружин, одной угловой и двух подвижных опор. Частица массой m расположена посередине между двумя линейных пружинами жёсткостью С1. Жёсткость угловой пружины С2. Опоры движутся навстречу друг другу с постоянной скоростью V.(Рис.1) Главной задача исследования данной модели является поиск уравнения движения частицы m и его численное решение. Считалось, что у частицы 1 степень свободы, зависящая от перемещения по вертикали, перемещение по горизонтали не учитывается.Уравнение движения
Для поиска уравнения движения частицы была найдена её потенциальная и киническая энергия, далее было использовано уравнение Лагранжа II рода. Было получено следующее дифференциальное уравнение 2 порядка, описывающее колебания частицы m.
- с2 – жёсткость угловой пружины
- с1 – жёсткость линейных пружин
- V – cкорость подвижных опор
- a – начальная длина пружины
- t – время
- m – масса частицы
Численное решение
Для поиска численного решения полученного дифференциального уравнения движения был использован пакет Wolfram Mathematica.Результаты можно видеть на графике зависимости перемещения частицы вдоль вертикальной оси от времени.
Список литературы
- Kuzkin V.A., Dannert M.M.: Dynamic buckling of a column under constant speed compression. Acta Mech (2016) 227:1645-1652.