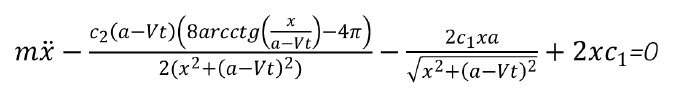Моделирование динамической потери устойчивости стержня при сжатии с постоянной скоростью
Курсовой проект по Механике дискретных сред
Исполнитель: Лосева Татьяна
Группа: 43604/1
Семестр: осень 2018
Содержание
Постановка задачи[править]
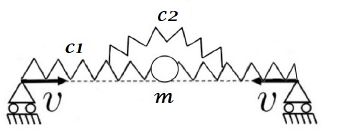
Рассматривалась простая одномерная модель, которая отражает основные физические характеристики стержня, подвергающегося сжатию с постоянной скоростью.Стержень моделируется с помощью частицы, двух линейных пружин, одной угловой и двух подвижных опор. Частица массой m расположена посередине между двумя линейных пружинами жёсткостью С1. Жёсткость угловой пружины С2. Опоры движутся навстречу друг другу с постоянной скоростью V.(Рис.1) Главной задача исследования данной модели является поиск уравнения движения частицы m и его численное решение. Считалось, что у частицы 1 степень свободы, зависящая от перемещения по вертикали, перемещение по горизонтали не учитывается.
Уравнение движения[править]
Для поиска уравнения движения частицы была найдена её потенциальная и киническая энергия, далее было использовано уравнение Лагранжа II рода. Было получено следующее дифференциальное уравнение 2 порядка, описывающее колебания частицы m.
- с2 – жёсткость угловой пружины
- с1 – жёсткость линейных пружин
- V – cкорость подвижных опор
- a – начальная длина пружины
- t – время
- m – масса частицы
Численное решение[править]
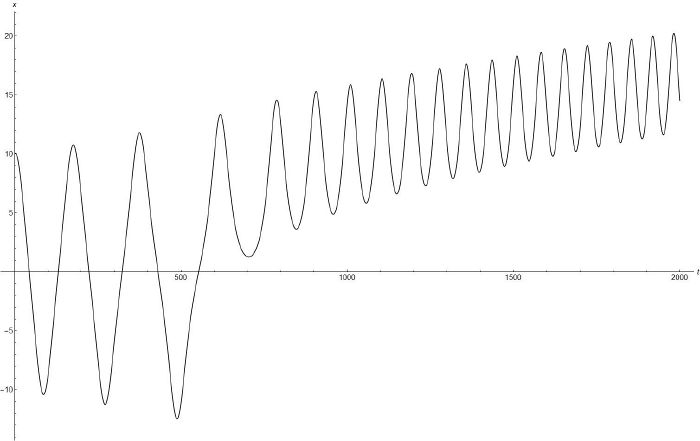
Для поиска численного решения полученного дифференциального уравнения движения был использован метод Эйлера.Результаты можно видеть на графике зависимости перемещения частицы вдоль вертикальной оси от времени.X - координата частицы по вертикальной оси,t - время.
На графике мы видим колебания системы около центрального положения равновесия (x=0), а при достижении критической силы в определенный момент времени можно заметить быстрое возрастание прогиба - происходит потеря устойчивости.
График взят при следующих параметрах :
- m = 10(масса частицы)
- c1 = 1(жесткость линейной пружины)
- c2 = 0.0001(жёсткость угловой пружины)
- a = 70(начальное расстояние между опорами)
- x0 = 10(начальные условия)
- V = 0.001(скорость)
Список литературы[править]
- Kuzkin V.A., Dannert M.M.: Dynamic buckling of a column under constant speed compression. Acta Mech (2016) 227:1645-1652.