Определение упругих свойств треугольной двумерной решётки с взаимодействиями Леннарда-Джонса

Курсовой проект по Механике дискретных сред

Исполнитель: Рубинова Раиса

Группа: 11 (43604/1)

Семестр: осень 2018

Постановка задачи

Рисунок 1. Двумерная треугольная решётка

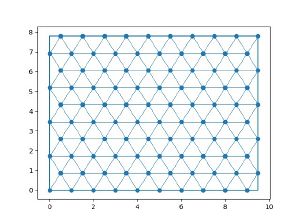
Смоделировать прямоугольную двумерную область при помощи треугольной решётки (рис. 1), частицы которой взаимодействуют между собой посредством потенциала Леннарда-Джонса. Экспериментально определить зависимость силы F, возникающей в решётке при растяжении, от величины относительной деформации ε.

Общие сведения

Потенциал Леннарда-Джонса

Парный силовой потенциал взаимодействия. Определяется формулой:

[math] \varPi(r) = D\left[\left(\frac{a}{r}\right)^{12}-\left(\frac{a}{r}\right)^{6}\right], [/math]

где

• [math]r[/math] — расстояние между частицами,
• [math]D[/math] — энергия связи,
• [math]a[/math] — длина связи.

Потенциал является частным случаем потенциала Ми и не имеет безразмерных параметров.

Сила взаимодействия, соответствующая потенциалу Леннард-Джонса, вычисляется по формуле

[math] F(r) = \frac{12D}{a}\left[-\left(\frac{a}{r}\right)^{13} + \left(\frac{a}{r}\right)^{7}\right]. [/math]

Решение

Данная задача может быть решена двумя способами.

Первый способ

Обе грани жёстко закреплены, растяжение происходит одномоментно и действует на все рассматриваемые частицы

[math] x = x(1 + ε) [/math]

В этом случае силы, действующие на частицы со стороны соседей, попробуют стянуть частицы по второй оси, по которой закрепление отсутствует, поэтому необходимо дать системе прийти в относительное состояние равновесия. После этого находится сила, действующая на частицу одной из закреплённых граней, и растяжение повторяется.

Именно данный способ реализован в уже существующей версии программы.

Второй способ

Одна грань жёстко закреплена по обеим осям, в то время как вторая перемещается с некоторой постоянной скоростью, достаточно маленькой, чтобы возмущение проходило по каждому элементу сетку.

Данный способ ещё не реализован, однако в дальнейшем планируется решить задачу определения зависимости силы от относительной деформации и при помощи этого варианта, после чего будет проведён сравнительный анализ двух способов.

Результаты

Рис. 2 Зависимость силы от относительных деформаций

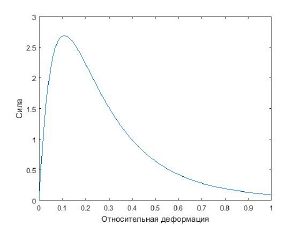
В результате моделирования был получен график зависимости силы, возникающей на закреплённой грани, от величины относительной деформации (рис. 2)

Дальнейшие планы

Сейчас реализован первый способ определения зависимости силы, возникающей на границах рассматриваемого прямоугольника, в зависимости от относительной деформации. В следующем семестре (весна 2019) планируется реализация второго способа, а также определение критических параметров растяжения получившегося материала.