Определение упругих свойств треугольной двумерной решётки с взаимодействиями Леннарда-Джонса

Курсовой проект по Механике дискретных сред

Исполнитель: Рубинова Раиса

Группа: 11 (43604/1)

Семестр: осень 2018

Основная страница: Курсовые проекты по ВМДС: 2018-2019

Постановка задачи

Рисунок 1. Двумерная треугольная решётка

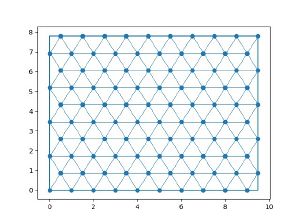
Смоделировать прямоугольную двумерную область при помощи треугольной решётки (рис. 1), частицы которой взаимодействуют между собой посредством потенциала Леннарда-Джонса. Экспериментально определить зависимость силы F, возникающей в решётке при растяжении, от величины относительной деформации ε.

Общие сведения

Потенциал Леннарда-Джонса

Парный силовой потенциал взаимодействия. Определяется формулой:

[math] \varPi(r) = D\left[\left(\frac{a}{r}\right)^{12}-\left(\frac{a}{r}\right)^{6}\right], [/math]

где

• [math]r[/math] — расстояние между частицами,
• [math]D[/math] — энергия связи,
• [math]a[/math] — длина связи.

Потенциал является частным случаем потенциала Ми и не имеет безразмерных параметров.

Сила взаимодействия, соответствующая потенциалу Леннард-Джонса, вычисляется по формуле

[math] F(r) = \frac{12D}{a}\left[-\left(\frac{a}{r}\right)^{13} + \left(\frac{a}{r}\right)^{7}\right]. [/math]

Решение

Данная задача может быть решена двумя способами.

Первый способ

Обе грани жёстко закреплены, растяжение происходит одномоментно и действует на все рассматриваемые частицы

[math] x = x(1 + ε) [/math]

В этом случае силы, действующие на частицы со стороны соседей, попробуют стянуть частицы по второй оси, по которой закрепление отсутствует, поэтому необходимо дать системе прийти в относительное состояние равновесия. После этого находится сила, действующая на частицу одной из закреплённых граней, и растяжение повторяется.

Именно данный способ реализован в уже существующей версии программы.

Второй способ

Одна грань жёстко закреплена по обеим осям, в то время как вторая перемещается с некоторой постоянной скоростью, достаточно маленькой, чтобы возмущение проходило по каждому элементу сетку.

Данный способ ещё не реализован, однако в дальнейшем планируется решить задачу определения зависимости силы от относительной деформации и при помощи этого варианта, после чего будет проведён сравнительный анализ двух способов.

Результаты

Рис. 2 Зависимость силы от относительной деформации

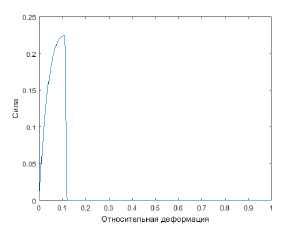
В результате моделирования первым способом был получен график зависимости силы, возникающей на закреплённой грани, от величины относительной деформации (рис. 2)