Manipulator model

Description

This is the page of a project related to project "Fencing".

Developers

Dzenushko Dainis

Global Task

The main aim of this project is development of a program which will be useful for recording and calculation of manipulator's movement.

Current task

Current task is development of fencer's hand model. That means to create mathematical model, that finds the position of a hand and comes to this position from any previous position with visualization on C# language, using parameters (changes of angles in joints and coordinates of a shoulder)

Some information about modelling

Degrees of freedom

This model has 9 degrees of freedom:
2 — translation movement of a shoulder (front/back; up/down)
3 — shoulder joint as a ball joint
1 — elbow joint 
1 — rotation of wrist round it’s axis
2 — wrist (2 perpendicular cylindrical joints)

Hand rotation

In order to rotate any 3D object we should rotate related vector.
But how to rotate vector?
This programm uses quaternions for vector rotation.

Quaternions

Usually quaternions are defined as a number system that extends the complex numbers to 4D space. In a simplier way we can define quaternions as 4 numbers with specific operations and properties.
[math]Q = (w,x,y,z) = w + xi + yj + zk[/math] , where i,j,k satisfies
[math]i^2 = j^2 = k^2 = ijk = -1[/math]

Useful formulas

We are going to use quaternion written as
[math]Q = [w,v][/math] - where [math]w[/math] - scalar and [math]v[/math] - vector
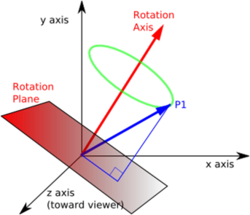
In these terms we have rotation quaternion
[math]Q = \left[ \cos \left( \frac{\alpha}{2} \right), \sin \left( \frac{\alpha}{2} \right)v \right][/math]
This is the quaternion that rotates round vector [math]v[/math] on angle [math]\alpha[/math]
[math]Q* = [w, -v][/math] - conjugated quaternion
[math]norm(Q) = \sqrt{w^2 + x^2 + y^2 +z^2}[/math] - norm of quaternion
[math]Q^{-1} = \frac{Q*}{norm(Q)}[/math] - reverse quaternion
[math]QQ' = [ ww' - v \cdot v', v \times v' + wv' + w' v][/math] - quaternion multiplication

Rotate vector

In order to rotate the vector [math]r[/math] we need to go through the following steps:
1) Cast vector to quaternion It's easy to make quaternion of vector. Just add zero to the scalar part and your vector to the vector part of quaternion
[math]R = [0,r][/math]
2) Multiply
[math]R' = Q R Q^{-1}[/math]
Now we have quaternion [math]R[/math] rotated.
3)Cast back After all we should cast quaternion [math]R'[/math] to vector [math]r'[/math]. It's as easy as first cast, just forget about scalar part. Vector part of [math]R'[/math] is ours [math]r'[/math] vector.

Rotation

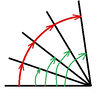
OK! We already can rotate any vector around any on any angle (but not bigger than 180deg)!
But it's not enough. We want to get motion and it should be smooth. So we need to go through many points between each position. There is a problem that appears if we try to rotate vector around two axis at the same time. Rotations are not additive, so we can't just rotate on a small angle each step. The solution is simple, we need to rotate vector on bigger angle on each step from the initial position.

About program interface

Because program doesn't have help yet, I should give some information about it's interface.
I'll tell about each tab:

Graph

This tab is responsible for visualization of movement. There are some keys working on this tab:
Up/Down – rotation around horizontal axis
Left/Right – rotation around vertical axis
Ctrl + Up/Down/Left/Right – faster rotation
+/- (OemPlus/OemMinus) –Foundation Zoom

• 



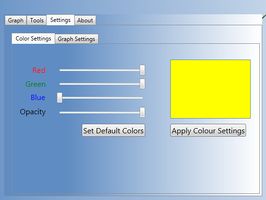
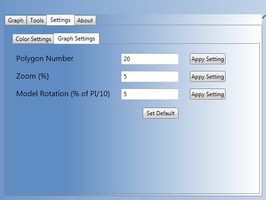
Settings

This one is responsible for customization of model appearance. You can change model color and opacity, quality and speed of basis rotation.

• 
• 



3D Graphics realization

Program interface is developed by using special library WPF (Windows Presentation Foundation) and Microsoft Visual Studio's built-in XAML redactor.

• What is WPF:
  

“The Windows Presentation Foundation is Microsoft’s next generation UI framework to create applications with a rich user experience. It is part of the .NET framework 3.0 and higher. WPF combines application UIs, 2D graphics, 3D graphics, documents and multimedia into one single framework. Its vector based rendering engine uses hardware acceleration of modern graphic cards. This makes the UI faster, scalable and resolution independent. etc.”

• Viewport3D element:
  

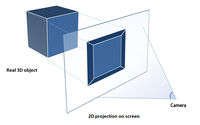
Graphics contents in 3-D WPF application is encapsulated in Viewport3D element, which can be placed on two-dimensional element such as program window. Graphics system identifies Viewport3D as two-dimensional visual element such as many in WPF. Viewport3D function as preview window of three-dimensional scene. More precisely it is projection of 3-D scene on plane (screen).

• Drawing 3D objects

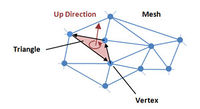
Drawing of objects is done by triangulation, that means that we need to build it of triangles. Notice that back side of triangles is transparent as default.

Maybe this can be used

This program in future can be used as a package for modelling manipulators. They are very similar to hand, so the idea is the same.

• 
• 
• 



Last Features

ver_1.0.0.33:

• Saving Graph settings to the binary file
• Rotation of hand parts
• Using quaternions instead of rotation tensors
• Rotation optimization

Future Features

Under development...

• Optimization of calculations related to rotation
• Switching to post-processing visualization instead of visualization and calculation at the same time
• Preparing the code for development of different manipulators
• Development of interface for user defined manipulators and movement

Last, sometimes stable version

ver_1.0.0.33:
Hand_Model_x86.zip
Hand_Model_x64.zip