Ковалев Олег. Курсовой проект по теоретической механике

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск

Тема проекта

Вычисление энергии напряженного состояния для платоновых углеводородов

Постановка задачи

Рассчитать энергию напряженного состояния для молекул тетраэдрана, кубана и додекаэдрана.

Общие сведения о платоновых углеводородах

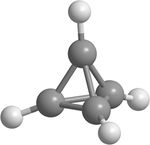
  • Тетраэдран

Представляет собой химическое соединение [math]C_4H_4[/math], в котором атомы углерода расположены в вершинах тетраэдра. Длина связи C-C равна 0,1522 нм, С-H равна 0,1068 нм. Проблема синтеза остается нерешенной.

Tetraedran
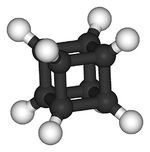
  • Кубан

Представляет собой химическое соединение [math]C_8H_8[/math], в котором атомы углерода расположены в вершинах куба. Длина связи C-C равна 0,157 нм, C-H равна 0,1082. Синтезированы.

Cubane
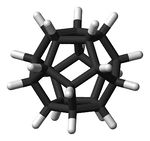
  • Додекаэдран

Представляет собой химическое соединение [math]C_20H_20[/math], в котором атомы углерода расположены в вершинах додекаэдра. Синтезированы.

Dodecahedrane

Решение

Рассмотрим следующую модель молекулы. Предположим, что связи между C-C можно заменить линейными пружинами жесткости [math] k = 660 H/m[/math] (соответствует графиту). Также, предположим, что связи C-C и С-С скреплены угловыми пружинами жесткости [math] c = 1,35 H*m[/math] (соответствует алмазу). Тогда упрощенное уравнение расчета энергии напряжения в рамка механической модели будет иметь следующий вид [?]:

[math] U=1/2kn_a(a - a_0)^2 + 1/2cn_\alpha(sin^2(\alpha - \alpha_0)), [/math]

Здесь каждое слагаемое относится к отдельным компонентам напряжения: деформациям расстояний (а) и валентных углов [math]\alpha[/math]. Тогда, в силу симметрии молекул, можно записать простые соотношение для энергии.

  • Для тэтраэдрана

[math] U_t=3k(a - a_0)^2 + 6c(sin^2(\alpha - \alpha_0)), [/math]

где [math]\alpha = 60^0[/math] - угол между связями C-C и С-H в молекуле тетраэдрана, [math]\alpha_0 = 109,5^0[/math] - угол между С-С и С-H, в недеформированном состоянии; [math]a[/math] - длина связи С-С в молекуле тетраэдрана, [math]a_0[/math] - длина связи C-C в алканах.

При подстановке значений получаем: [math] U_t=5,4 eV/at, [/math]

  • Для кубана

[math] U_k=6k(a - a_0)^2 + 12c(sin^2(\alpha - \alpha_0)), [/math]

где [math]\alpha = 90^0[/math] - угол между связями C-C и С-H в молекуле кубана, [math]\alpha_0 = 109,5^0[/math] - угол между С-С и С-H, в недеформированном состоянии; [math]a[/math] - длина связи С-С в молекуле кубана, [math]a_0[/math] - длина связи C-C в алканах.

При подстановке значений получаем: [math] U_t=11,3 eV/at, [/math]

  • Для додекаэдрана

[math] U_d=15k(a - a_0)^2 + 30c(sin^2(\alpha - \alpha_0)), [/math]

где [math]\alpha = 108^0[/math] - угол между связями C-C и С-H в молекуле додекаэдрана, [math]\alpha_0 = 109,5^0[/math] - угол между С-С и С-H, в недеформированном состоянии; [math]a[/math] - длина связи С-С в молекуле додекаэдрана, [math]a_0[/math] - длина связи C-C в алканах.

При подстановке значений получаем: [math] U_t=12.6 eV/at, [/math]

Обсуждение результатов и выводы

В результате работы били вычислены потенциальные энергии тетраэдрана, кубана и додекаэдрана. Значение энергии для тетраэдрана отличается от результатов, полученных в работе [3] на 37%, для кубана на 60% [1]. Данные расхождения вероятно связаны с ошибкой модели.

Ссылки по теме

  • 1. Термическая устойчивость кубана C8H8. М.М. Маслов, Д.А. Лобанов, А.И. Подливаев, Л.А. Опенов. http://journals.ioffe.ru/ftt/2009/03/p609-612.pdf
  • 2. Термическая устойчивость линейных олигомеров, построенных из кубиленовых единиц. М.М. Маслов. http://journals.ioffe.ru/ftt/2009/03/p609-612.pdf
  • 3. Термическая устойчивость молекулы тетраэдрана C4H4. М.М. Маслов.
  • 4. Description of elastic properties of diamond using angular atomic interaction. S. S. Khakalo A. M. Krivtsov O. S. Loboda.
  • "Фуллерены С20 и С60"

См. также

Источник — «http://tm.spbstu.ru/?title=Ковалев_Олег._Курсовой_проект_по_теоретической_механике&oldid=12549»