Асонов Игорь: Моделирование деформирования и разрушения хрупких гранулированных материалов методом динамики частиц
Проект посвящен созданию DEM(MD)-модели, которая бы корректно учитывала наличие полимерного мостика между керамическими частицами. Работа с проектом ведется параллельно с Michael Szelwis: "Modeling the plastic behavior of ceramic-polymer-composites".
Содержание
Существующие DEM-модели
Как правило (cсылки), в подобных композитных системах для моделирования связи между частицами в механике дискретных сред используются подходы, основанные на Bonded-Particle Model предложенной Potyondy D.O. и Cundall P.A. [1].
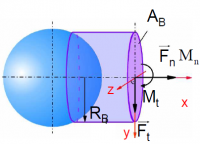
Bonded-Particle Model заключается в инкрементальном изменении сил и моментов, действующих со стороны связи на частицу, согласно следующим уравнениям:
, где - приращение за шаг интегрирования нормальной и тангенциальной составляющей силы, действующей со стороны связи, - приращение за шаг интегрирования нормальной и тангенциальной составляющей момента, действующего со стороны связи, - площадь поперечного сечения связи, - момент инерции сечения связи относительно оси z, - радиус связи, - нормальная и тангенциальная проекция относительной поступательной скорости частиц соответственно, - нормальная и тангенциальная проекция относительной угловой скорости частиц соответственно, - нормальная и сдвиговая жесткость связи соотвественно, - шаг интегрирования. При моделировании представленные выше силы и моменты со стороны связи складываются с силами и моментами Hertz-Mindlin'a[2], которые возникают только при физическом контакте частиц.
Недостатки существующих моделей
- Интегрирование вектора угловой скорости не равно углу поворота (Так ли это?). Следовательно момент со стороны связи на частицу считается не как линейная пружина. С поступательным движением таких проблем нет и можно показать, что суммарная сила со стороны связи на частицу равна , где - жесткость линейной пружины, - вектор, соединяющий частицы в момент создания связи, - вектор, соединяющий частицы в данный момент времени.
- С использованием BPM сложно (если вообще возможно) использовать нелинейный закон межчастичного взаимодействия.
Спросить у Michael Wolff
Предлагаемое решение
Использовать V-model предложенную Виталием Кузькиным. В качестве программного пакета в котором будет осуществляться моделирование механических свойств керамико-полимерных композитов был выбран коммерческий пакет EDEM. Реализацией V-model для EDEM в качестве подключающейся библиотеки контактных взаимодействий я сейчас и занимаюсь.
Ссылки
- ↑ Potyondy D. O. and Cundall P. A, A bonded-particle model for rock. International Journal of Rock Mechanics and Mining Sciences, 41, 1329-1364 (2004) pdf
- ↑ Alberto Di Renzo, Francesco Paolo Di Maio, Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes. Chemical Engineering Science, 59 525 – 541, (2004)