Ковалев Олег. Курсовой проект по теоретической механике

Материал из Department of Theoretical and Applied Mechanics
Версия от 17:14, 16 июня 2012; 37.144.36.61 (обсуждение) (→‎Обсуждение результатов и выводы)

Перейти к: навигация, поиск

Тема проекта

Вычисление энергии напряженного состояния для платоновых углеводородов

Постановка задачи

Рассчитать энергию напряженного состояния для молекул тетраэдрана, кубана и додекаэдрана.

Общие сведения о платоновых углеводородах

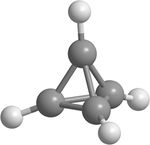
  • Тетраэдран

Представляет собой химическое соединение [math]C_4H_4[/math], в котором атомы углерода расположены в вершинах тетраэдра. Длина связи C-C равна 0,1522 нм, С-H равна 0,1068 нм. Проблема синтеза остается нерешенной.

Tetraedran
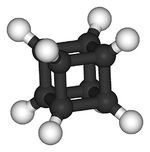
  • Кубан

Представляет собой химическое соединение [math]C_8H_8[/math], в котором атомы углерода расположены в вершинах куба. Длина связи C-C равна 0,157 нм, C-H равна 0,1082. Синтезированы.

Cubane
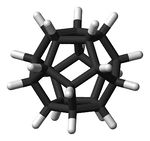
  • Додекаэдран

Представляет собой химическое соединение [math]C_{20}H_{20}[/math], в котором атомы углерода расположены в вершинах додекаэдра. Синтезированы.

Dodecahedrane

Решение

Существует три подхода расчета энергии напряжения: экспериментальный, основанный на вычислении тепловой энергии, образующейся при сжигании материала; приближенные квантовохимические расчеты; методом расчета механической модели молекулы [6]. В данной работе используется третий подход.

Рассмотрим следующую модель молекулы. Предположим, что связи между C-C можно заменить линейными пружинами жесткости [math] k = 660 H/m[/math] (соответствует графиту). Также, предположим, что связи C-C и С-С скреплены угловыми пружинами жесткости [math] c = 1,35\cdot 10^{-18} H\cdot m[/math] (соответствует алмазу). Тогда упрощенное уравнение расчета энергии напряжения в рамка механической модели будет иметь следующий вид [5]:

[math] U=1/2kn_a(a - a_0)^2 + 1/2cn_\alpha(sin^2(\alpha - \alpha_0)), [/math]

Здесь каждое слагаемое относится к отдельным компонентам напряжения: деформациям расстояний ([math]a[/math]) и валентных углов [math]\alpha[/math]. Тогда, в силу симметрии молекул, можно записать простые соотношение для энергии.

  • Для тэтраэдрана

[math] U_t=3k(a - a_0)^2 + 6c(sin^2(\alpha - \alpha_0)), [/math]

где [math]\alpha = 60^0[/math] - валентный угол в молекуле тетраэдрана, [math]\alpha_0 = 109,5^0[/math] - валентный угол в недеформированном состоянии; [math]a[/math] - длина связи С-С в молекуле тетраэдрана, [math]a_0[/math] - длина связи C-C в алканах.

  • Для кубана

[math] U_k=6k(a - a_0)^2 + 12c(sin^2(\alpha - \alpha_0)), [/math]

где [math]\alpha = 90^0[/math] - валентный угол в молекуле кубана, [math]\alpha_0 = 109,5^0[/math] - валентный угол в недеформированном состоянии; [math]a[/math] - длина связи С-С в молекуле кубана, [math]a_0[/math] - длина связи C-C в алканах.

  • Для додекаэдрана

[math] U_d=15k(a - a_0)^2 + 30c(sin^2(\alpha - \alpha_0)), [/math]

где [math]\alpha = 108^0[/math] - валентный угол между в молекуле додекаэдрана, [math]\alpha_0 = 109,5^0[/math] - валентный угол в недеформированном состоянии; [math]a[/math] - длина связи С-С в молекуле додекаэдрана, [math]a_0[/math] - длина связи C-C в алканах.

Обсуждение результатов и выводы

Молекула Длина связи, nm Валентный угол Энергия напряжения, kcal/mol
Тэтраэдран
0.152
[math]60.0^0[/math]
676.0
Кубан
0.157
[math]90.0^0[/math]
265.3
Додекаэдран
0.154
[math]108.0^0[/math]
4.0
Алмаз
0.154
[math]109.5^0[/math]
0.0
Вещество Энергия, kcal/mol
Пентан
838.7
Бензин
Тратил

В результате работы били вычислены энергии напряжения для тетраэдрана, кубана и додекаэдрана (значения приведены в таблице). Из таблицы видно, что с ростом валентного угла, растет энергия напряжения. Это связано с тем, что основной вклад в энергию вносят деформации валентных углов (у додекаэдрана наименьшая, у тетраэдрана наибольшая). Вклад межатомных связей мал, так как мала их деформация. Значение энергии для кубана отличается от значения 150 kcal/mol, приведенного в работе [6] на 43%, однако в работе не указан способ получения данного значения.

Ссылки по теме

См. также

Источник — «http://tm.spbstu.ru/?title=Ковалев_Олег._Курсовой_проект_по_теоретической_механике&oldid=13010»