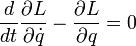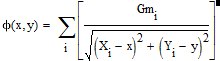КП: Движение спутника в двойной системе — различия между версиями

Версия 21:41, 2 июня 2015

Курсовой проект по Теоретической механике

Исполнитель: Мущак Никита

Группа: 09 (23604)

Семестр: весна 2015

Модель системы

Формулировка задачи

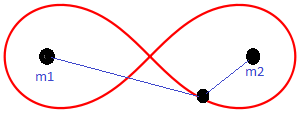
Исследовать движение спутника двойной системы. Двойная система состоит из 2 неподвижных планет и спутника вращающегося вокруг них как показано на рисунке сверху. Определить стационарные орбиты спутника, а также устойчивость движения спутника.

Общие сведения по теме

Задачи подобного рода можно решать разными способами. Но решать данную задачу будем 2 способами :

с помощью уравнения Лагража 2-ого рода и как упрощенная задача 3-х тел

1 способ: уравнение Лагранжа 2-ого рода:

,где L - функция Лагранжа (лагранжиан),q- обобщенная координата, t — время, i— число степеней свободы механической системы

Функцию Лагранжа будем считать как разность кинетической и потенциальной энергий системы.

Дальнейшим дифференцированием получаем уравнение движения.

2 способ:записываем 2-ой закон Ньютона для данной задачи и получаем:

,где - гравитационная постоянная,m- массы планет,q - координаты планет.

Решение

Ланранжиан будет иметь вид: , где m - масса спутника, q - обобщенная координата, - потенциал гравитационного поля.

Подставляя полученное выражение в уравнение Лагранжа, можно получить уравнение движения:

Как можно заметить из уравнения движения масса спутника никак не влияет на траекторию.

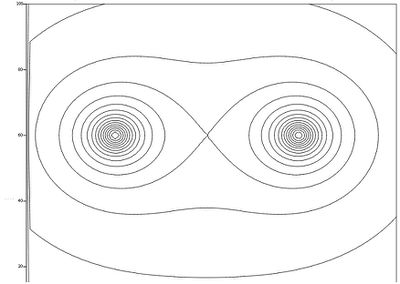
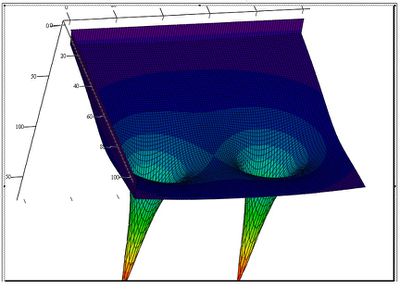
Отдельного рассмотрения заслуживает конфигурация потенциального гравитационного поля.

Оно будет иметь вид:

При этом графики такого поля будут выглядеть:

Контурный график

Сравнение с овалами Кассини

3D график

Стационарные орбиты спутника будут близки к овалам Кассини

-это семейство кривых, которые задаются уравнением , где 2c-расстояние между фокусами, а- некоторая константа.

графики овалов Кассини:

Частным случаем овалов Кассини является лемниската Бернулли, которая выглядит как знак бесконечности или восьмерка

В случае трех материальных тел на каждое из них действуют две силы со стороны двух других тел. Например, на тело m₁ действуют следующие силы (F₂ и F₃):

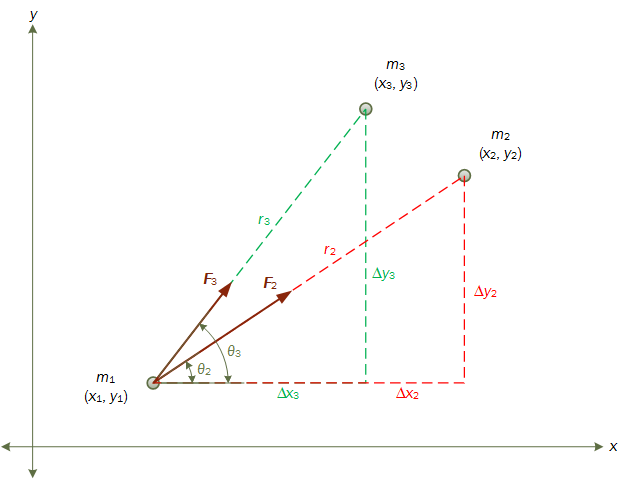
Сначала заметим, что результирующая силаF₁, действующая на тело m₁, будет суммой сил F₂ и F₃. Это значит, что F₁ = m₁a₁ = F₂ + F₃.

Обсуждение результатов и выводы

Скачать отчет:
Скачать презентацию:Движение спутника в двойной системе

Ссылки по теме

См. также

• Справочная информация
• Курсовые проекты ТМ