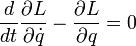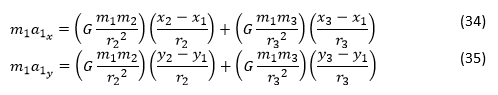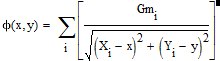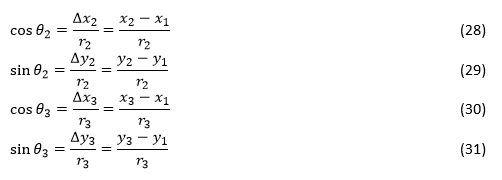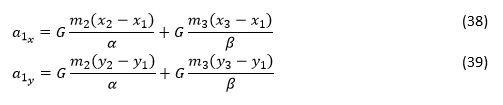КП: Движение спутника в двойной системе
Курсовой проект по Теоретической механике
Исполнитель: Мущак Никита
Группа: 09 (23604)
Семестр: весна 2015
Содержание
Аннотация проекта[править]
Данный проект посвящен изучению движения спутника в двойной системе под действием гравитации. В ходе работы над проектом была написана программа, которая моделирует процесс движения спутника. Программа написана на языке JavaScript.
Формулировка задачи[править]
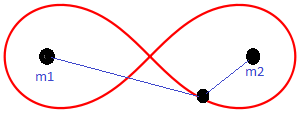
Исследовать движение спутника двойной системы под действием гравитационной силы. Двойная система состоит из 2 неподвижных планет и спутника вращающегося вокруг них как показано на рисунке сверху. Определить стационарные орбиты спутника, а также устойчивость движения спутника.
Общие сведения по теме[править]
Задачи подобного рода можно решать разными способами. Но решать данную задачу будем 2 способами :
с помощью уравнения Лагража 2-ого рода и как упрощенная задача 3-х тел
1 способ: уравнение Лагранжа 2-ого рода:
,где L - функция Лагранжа (лагранжиан),q- обобщенная координата, t — время, i— число степеней свободы механической системы
Функцию Лагранжа будем считать как разность кинетической и потенциальной энергий системы.
Дальнейшим дифференцированием получаем уравнение движения.
2 способ: записываем 2-ой закон Ньютона для данной задачи и получаем:
, где G- гравитационная постоянная,m- массы планет.
Решение[править]
Ланранжиан будет иметь вид:
![]() , где m - масса спутника, q - обобщенная координата,
, где m - масса спутника, q - обобщенная координата,
![]() - потенциал гравитационного поля.
- потенциал гравитационного поля.
Подставляя полученное выражение в уравнение Лагранжа, можно получить уравнение движения:
![]()
Как можно заметить из уравнения движения масса спутника никак не влияет на траекторию.
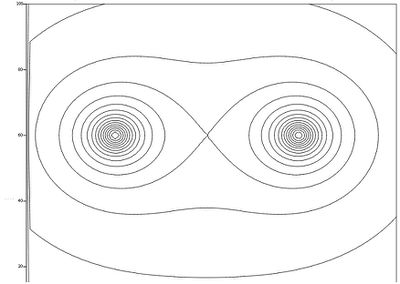
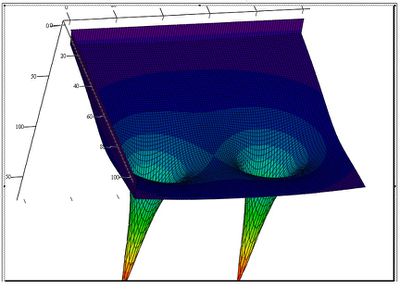
Отдельного рассмотрения заслуживает конфигурация потенциального гравитационного поля.
При этом графики такого поля будут выглядеть:
Стационарные орбиты спутника будут близки к овалам Кассини
-это семейство кривых, которые задаются уравнением ![]() , где 2c-расстояние между фокусами, а- некоторая константа.
, где 2c-расстояние между фокусами, а- некоторая константа.
Частным случаем овалов Кассини является лемниската Бернулли, которая выглядит как знак бесконечности или восьмерка
Программа: скачать
Файл "K3.html"
1 <!DOCTYPE html>
2
3 <html>
4 <head>
5 <meta charset="utf-8" />
6 <meta http-equiv="X-UA-Compatible" content="IE=Edge" /> <!-- For IE on an intranet. -->
7 <title>Moon in Binary System</title>
8 <style>
9 html, body {
10 margin: 0;
11 padding: 0;
12 }
13
14 html {
15 overflow-y: scroll; /* There's an issue with the scrollbar "randomly" appearing - this just keeps it always visible in case the user is using a very wide and narrow monitor. */
16 }
17
18 body {
19 width: 1024px; /* Currently, most screens can handle this. */
20 margin: auto; /* Center the page content. */
21 background-color: #777;
22 font-family: "Segoe UI", Tahoma, Geneva, Verdana, sans-serif; /* Start screen font. */
23 }
24
25 header {
26 color: #FFF;
27 text-shadow: 5px 5px 10px #333;
28 }
29
30 section {
31 position: relative; /* Float children relative to this element. */
32 }
33
34 section form {
35 width: 210px; /* This is a bit less than the "section #WebGLCanvasElementContainer margin-left" value to provide a nice space between the form and the viewport. */
36 float: left;
37 text-align: center; /* Center the button elements. */
38 }
39
40 section form fieldset {
41 text-align: left; /* Undo the button center aligning trick for the text in the form. */
42 margin-bottom: 1.25em; /* Adjust this so that the height of the form is about the same height as the WebGL Three.js viewport element. */
43 }
44
45 section form fieldset input {
46 width: 100%;
47 }
48
49 section form td {
50 white-space: nowrap; /* Don't let words like "x-position" break at the hyphen (which occurs in Chrome). */
51 }
52
53 section #WebGLCanvasElementContainer {
54 border: 1px solid #DDD; /* Match the native color of the fieldset border. */
55 width: 800px; /* The assumed fixed width of the WebGL Three.js viewport element. */
56 height: 600px; /* The assumed fixed height of the WebGL Three.js viewport element. */
57 margin-left: 224px; /* This is "body width" minus "section #WebGLCanvasElementContainer width" or 1024px - 800px = 224px. */
58 background-image: url('starField.jpg'); /* 0.15 opacity value. */
59 }
60
61 section article {
62 padding: 0 1em;
63 color: white;
64 }
65
66 section button {
67 width: 4.5em;
68 }
69 </style>
70 <script>
71 /*// Preload all images/bitmaps.
72 var preloadImages = [];
73 var preloadImagePaths = ["jupiter.png", "saturn.png", "moon.png", "starField.jpg", "starField.jpg"];
74
75 for (var i = 0; i < preloadImagePaths.length; i++) {
76 preloadImages[i] = new Image();
77
78 preloadImages[i].onerror = function() {
79 if (console) {
80 console.error(this.src + " error.");
81 } // if
82 }; // onerror
83
84 preloadImages[i].src = preloadImagePaths[i]; // Preload images to improve perceived app speed.
85 } // for
86 */</script>
87 </head>
88
89 <body>
90 <header>
91 <h1>Moon in Binary System </h1>
92 </header>
93 <section>
94 <form id="initialConditions">
95 <fieldset>
96 <legend>Moon</legend>
97 <table id="mass1">
98 <tr>
99 <td>mass:</td>
100 <td><input id="m1_mass" type="number" value="1E18" required="required" /></td>
101 </tr>
102 <tr>
103 <td>x-position:</td>
104 <td><input id="m1_position_x" type="number" value="-141" required="required" /></td>
105 </tr>
106 <tr>
107 <td>y-position:</td>
108 <td><input id="m1_position_y" type="number" value="0" required="required" /></td>
109 </tr>
110 <tr>
111 <td>x-velocity:</td>
112 <td><input id="m1_velocity_x" type="number" value="0" required="required" /></td>
113 </tr>
114 <tr>
115 <td>y-velocity:</td>
116 <td><input id="m1_velocity_y" type="number" value="2" required="required" /></td>
117 </tr>
118 <tr style="display: none;">
119 <td>bitmap:</td>
120 <td><input type="text" value="moon.png" required="required" /></td>
121 </tr>
122 </table>
123 </fieldset>
124 <fieldset>
125 <legend>1st star</legend>
126 <table id="mass2">
127 <tr>
128 <td>mass:</td>
129 <td><input type="number" value="1E19" required="required" /></td>
130 </tr>
131 <tr>
132 <td>x-position:</td>
133 <td><input type="number" value="-100" required="required" /></td>
134 </tr>
135 <tr>
136 <td>y-position:</td>
137 <td><input type="number" value="0" required="required" /></td>
138 </tr>
139 <tr>
140 <td>x-velocity:</td>
141 <td><input type="number" value="0" required="required" /></td>
142 </tr>
143 <tr>
144 <td>y-velocity:</td>
145 <td><input type="number" value="0" required="required" /></td>
146 </tr>
147 <tr style="display: none;">
148 <td>bitmap:</td>
149 <td><input type="text" value="jupiter.png" required="required" /></td>
150 </tr>
151 </table>
152 </fieldset>
153 <fieldset>
154 <legend>2nd star</legend>
155 <table id="mass3">
156 <tr>
157 <td>mass:</td>
158 <td><input type="number" value="1E19" required="required" /></td>
159 </tr>
160 <tr>
161 <td>x-position:</td>
162 <td><input type="number" value="100" required="required" /></td>
163 </tr>
164 <tr>
165 <td>y-position:</td>
166 <td><input type="number" value="0" required="required" /></td>
167 </tr>
168 <tr>
169 <td>x-velocity:</td>
170 <td><input type="number" value="0" required="required" /></td>
171 </tr>
172 <tr>
173 <td>y-velocity:</td>
174 <td><input type="number" value="0" required="required" /></td>
175 </tr>
176 <tr style="display: none;">
177 <td>bitmap:</td>
178 <td><input type="text" value="saturn.png" required="required" /></td>
179 </tr>
180 </table>
181 </fieldset>
182 <button id="submitButton">Submit</button>
183 <button id="reloadButton">Reload</button>
184
185 </form>
186 <div id="WebGLCanvasElementContainer">
187 <!-- Three.js will add a canvas element to the DOM here. -->
188 <!-- The following <article> element (along with its content) will be removed via JavaScript just before the simulation starts: -->
189 <article>
190 <h2></h2>
191 <p>
192
193 </p>
194 <h2>Running the simulation</h2>
195 <ul>
196 <li>To start the simulation with the current set of initial conditions, click the <strong>Submit</strong> button.</li>
197 <li>To orbit, left-click and drag the mouse.</li>
198 <li>To pan, right-click and drag the mouse.</li>
199 <li>To zoom, roll the mouse wheel.</li>
200 <li>To enter your own initial conditions, enter numeric values of your choice (in the form to the left) and click <strong>Submit</strong>.
201 Note that large values such as 10<sup>18</sup> can be entered as 1E18.</li>
202 <li>To restart the simulation from scratch, click the <strong>Reload</strong> button (equivalent to refreshing the page).</li>
203 <li>For additional information and resources, click the <strong>Info</strong> button.</li>
204 </ul>
205 </article>
206 </div>
207 </section>
208 <script src="https://rawgithub.com/mrdoob/three.js/master/build/three.js"></script> <!-- The "CDN" for Three.js -->
209 <script src="https://rawgithub.com/mrdoob/three.js/master/examples/js/controls/OrbitControls.js"></script> <!-- Allows for orbiting, panning, and zooming. -->
210 <script>
211 var DENSITY= 1.38E14; // This value determined qualitatively by observing how large the spheres look onscreen (i.e., their radii).
212
213 document.getElementById('submitButton').addEventListener('click', handleSubmitButton, false);
214 document.getElementById('reloadButton').addEventListener('click', handleReloadButton, false);
215
216
217 var simulation = Simulation(); // Call the Simulation constructor to create a new simulation object.
218
219 function Simulation() { // A constructor.
220 var that = {}; // The object returned by this constructor.
221 var worker; // Will contain a reference to a fast number-chrunching worker thread that runs outside of this UR/animation thread.
222 var requestAnimationFrameID = null; // Used to cancel a prior requestAnimationFrame request.
223 var gl = {}; // Will contain WebGL related items.
224
225 gl.viewportWidth = 800; // The width of the Three.js viewport.
226 gl.viewportHeight = 600; // The height of the Three.js viewport.
227
228 gl.cameraSpecs = {
229 aspectRatio: gl.viewportWidth / gl.viewportHeight, // Camera frustum aspect ratio.
230 viewAngle: 50 // Camera frustum vertical field of view, in degrees.
231 };
232
233 gl.clippingPlane = {
234 near: 0.1, // The distance of the near clipping plane (which always coincides with the monitor).
235 far: 1000 // The distance of the far clipping plane (note that you get a negative far clipping plane for free, which occurs at the negative of this value).
236 };
237
238 gl.quads = 32; // Represents both the number of vertical segments and the number of horizontal rings for each mass's sphere wireframe.
239
240 gl.renderer = window.WebGLRenderingContext ? new THREE.WebGLRenderer({ alpha: true }) : new THREE.CanvasRenderer({ alpha: true }); // If WebGL isn't supported, fallback to using the canvas-based renderer (which most browsers support). Note that passing in "{ antialias: true }" is unnecessary in that this is the default behavior. However, we pass in "{ alpha: true }" in order to let the background PNG image shine through.
241 gl.renderer.setClearColor(0x000000, 0); // Make the background completely transparent (the actual color, black in this case, does not matter) so that the PNG background image can shine through.
242 gl.renderer.setSize(gl.viewportWidth, gl.viewportHeight); // Set the size of the renderer.
243
244 gl.scene = new THREE.Scene(); // Create a Three.js scene.
245
246 gl.camera = new THREE.PerspectiveCamera(gl.cameraSpecs.viewAngle, gl.cameraSpecs.aspectRatio, gl.clippingPlane.near, gl.clippingPlane.far); // Set up the viewer's eye position.
247 gl.camera.position.set(0, 450, 0); // The camera starts at the origin, so move it to a good position.
248 gl.camera.lookAt(gl.scene.position); // Make the camera look at the origin of the xyz-coordinate system.
249
250 gl.controls = new THREE.OrbitControls(gl.camera, gl.renderer.domElement); // Allows for orbiting, panning, and zooming via OrbitsControls.js by http://threejs.org. For an example, see http://threejs.org/examples/misc_controls_orbit.html.
251
252 gl.pointLight = new THREE.PointLight(0xFFFFFF); // Set the color of the light source (white).
253 gl.pointLight.position.set(0, 250, 250); // Position the light source at (x, y, z).
254 gl.scene.add(gl.pointLight); // Add the light source to the scene.
255
256 gl.spheres = []; // Will contain WebGL sphere mesh objects representing the point masses.
257
258 var init = function (initialConditions) { // Public method, resets everything when called.
259 if (requestAnimationFrameID) {
260 cancelAnimationFrame(requestAnimationFrameID); // Cancel the previous requestAnimationFrame request.
261 }
262
263 if (worker) {
264 worker.terminate(); // Terminate the previously running worker thread to ensure a responsive UI.
265 }
266 worker = new Worker('K3.js'); // Spawn a fast number-chrunching thread that runs outside of this UR/animation thread.
267
268 document.getElementById('WebGLCanvasElementContainer').style.backgroundImage = "url('starField.jpg')"; // Switch back to the non-opaque PNG background image.
269 document.getElementsByTagName('article')[0].style.display = "none"; // Remove from page-flow the one (and only) article element (along with all of its content).
270 document.getElementById('WebGLCanvasElementContainer').appendChild(gl.renderer.domElement); // Append renderer element to DOM.
271
272 while (gl.spheres.length) { // Remove any prior spheres from the scene and empty the gl.spheres array:
273 gl.scene.remove(gl.spheres.pop());
274 } // while
275
276 for (var i = 0; i < initialConditions.length; i++) { // Set the sphere objects in gl.spheres to initial conditions.
277 initializeMesh(initialConditions[i]); // This call sets the gl.spheres array.
278 } // for
279
280 worker.postMessage({
281 cmd: 'init', // Pass the initialization command to the web worker.
282 initialConditions: initialConditions // Send a copy of the initial conditions to the web worker, so it can initialize its persistent global variables.
283 }); // worker.postMessage
284
285 worker.onmessage = function (evt) { // Process the results of the "crunch" command sent to the web worker (via this UI thread).
286 for (var i = 0; i < evt.data.length; i++) {
287 gl.spheres[i].position.x = evt.data[i].p.x;
288 gl.spheres[i].position.z = evt.data[i].p.y;
289 gl.spheres[i].position.y = 0; // 3BodyWorker.js is 2D (i.e., the physics are constrained to a plane).
290 gl.spheres[i].rotation.y += initialConditions[i].rotation; // Place worker.onmessage in the init method in order to access its initialConditions array.
291 }
292 gl.renderer.render(gl.scene, gl.camera); // Update the positions of the masses (sphere meshes) onscreen based on the data returned by 3BodyWorker.js.
293 }; // worker.onmessage
294
295 function initializeMesh(initialCondition) {
296 var texture = THREE.ImageUtils.loadTexture(initialCondition.bitmap); // Create texture object based on the given bitmap path.
297 var material = new THREE.MeshPhongMaterial({ map: texture }); // Create a material (for the spherical mesh) that reflects light, potentially causing sphere surface shadows.
298 var geometry = new THREE.SphereGeometry(initialCondition.radius, gl.quads, gl.quads); // Radius size, number of vertical segments, number of horizontal rings.
299 var mesh = new THREE.Mesh(geometry, material); // A mesh represents the object (typically composed of many tiny triangles) to be displayed - in this case a hollow sphere with a bitmap on its surface.
300
301 mesh.position.x = initialCondition.position.x;
302 mesh.position.z = initialCondition.position.y; // Convert from 2D to "3D".
303 mesh.position.y = 0; // The physics are constrained to the xz-plane (i.e., the xy-plane in 3BodyWorker.js).
304
305 gl.scene.add(mesh); // Add the sphere to the Three.js scene.
306 gl.spheres.push(mesh); // Make the Three.js mesh sphere objects accessible outside of this helper function.
307 } // initializeMesh
308 } // init
309 that.init = init; // This is what makes the method public.
310
311 var run = function () { // Public method.
312 worker.postMessage({
313 cmd: 'crunch' // This processing occurs between animation frames and, therefore, is assumed to take a relatively small amount of time (as compared to current frame rates).
314 }); // worker.postMessage
315 gl.controls.update(); // Allows for orbiting, panning, and zooming.
316 requestAnimationFrameID = requestAnimationFrame(run); // Allow for the cancellation of this requestAnimationFrame request.
317 }; // run()
318 that.run = run;
319
320 return that; // The object returned by the constructor.
321 } // Simulation
322
323 function handleSubmitButton(evt) {
324 var m1 = InitialCondition(document.getElementById('mass1').querySelectorAll('input')); // A constructor returning an initial condition object.
325 var m2 = InitialCondition(document.getElementById('mass2').querySelectorAll('input'));
326 var m3 = InitialCondition(document.getElementById('mass3').querySelectorAll('input'));
327
328 evt.preventDefault(); // Don't refresh the page when the user clicks this form button.
329
330 if (!window.WebGLRenderingContext) { displayCanvasRendererWarning(); } // If necessary, warn the user that they're using a canvas-based Three.js renderer and that they should upgrade their browser so that a faster WebGL-based renderer can be used instead.
331 ///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
332 simulation.init([m1, m2, m3]);
333 ///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
334 simulation.run(); // The images have been preloaded so this works immediately.
335
336 function InitialCondition(inputElements) {
337 var mass = parseFloat(inputElements[0].value);
338
339 return {
340 mass: mass,
341 radius: calculateRadius(mass),
342 rotation: calculateRotation(mass),
343 position: { x: parseFloat(inputElements[1].value), y: parseFloat(inputElements[2].value) },
344 velocity: { x: parseFloat(inputElements[3].value), y: parseFloat(inputElements[4].value) },
345 bitmap: inputElements[5].value // This is a string value (hence the non-use of parseFloat).
346 };
347
348 function calculateRadius(mass) {
349 /*
350 Mass equals density times volume or m = D * V = D * (4/3 * PI * r^3), and solving for r = [(3 * m)/(4 * PI * D)]^(1/3)
351 */
352 var radicand = (3 * mass) / (4 * Math.PI * DENSITY); // Only change the value of DENSITY to affect the value returned by this function.
353
354 return Math.pow(radicand, 1 / 3);
355 } // calculateRadius
356
357 function calculateRotation(mass) {
358 /*
359 Using a power model, let the x-axis represent the radius and the y-axis the rotational rate of the sphere.
360 The power model is y = a * x^b, where a and b are constants (which were empirically derived).
361 */
362 var radius = calculateRadius(mass);
363
364 return 1.7 * Math.pow(radius, -1.9); // Rotational rate as a function of the sphere's radius.
365 } // calculateRotation
366 } // InitialCondition
367 } // handleSubmitButton
368
369 function handleReloadButton(evt) {
370 /*
371 Clicking a form button automatically refreshes the page, which is exactly the behavior we want (i.e., location.reload() is not necessary here).
372 */
373 } // handleReloadButton
374
375 function handleInfoButton(evt) {
376 /*
377 Note that when the info page covers up the animation, the animation stops because this is how requestAnimationFrame works. In this sense, we get a free pause feature.
378 */
379 evt.preventDefault(); // Don't refresh the page when the user clicks this form button.
380 window.open("info.html"); // Open the info.html page in another tab.
381 } // handleInfoButton
382
383 function displayCanvasRendererWarning() { // This assumes that the user's browser at least supports canvas.
384 var articleElement = document.getElementsByTagName('article')[0];
385
386 articleElement.innerHTML = "<h2>WebGL not supported, using canvas-based renderer, please upgrade your browser.</h2>";
387 articleElement.style.display = "block";
388 }
389 </script>
390 </body>
391 </html>
Файл "K3.js"
1 /*
2 The acceleration equations for the 2D three-body problem (see equations 42 through 50):
3
4 d^2[x1]/dt^2 = G*m2*(x2 - x1)/alpha + G*m3*(x3 - x1)/beta
5
6 d^2[y1]/dt^2 = G*m2*(y2 - y1)/alpha + G*m3*(y3 - y1)/beta
7
8 d^2[x2]/dt^2 = G*m1*(x1 - x2)/alpha + G*m3*(x3 - x2)/gamma
9
10 d^2[y2]/dt^2 = G*m1*(y1 - y2)/alpha + G*m3*(y3 - y2)/gamma
11
12 d^2[x3]/dt^2 = G*m1*(x1 - x3)/beta + G*m2*(x2 - x3)/gamma
13
14 d^2[y3]/dt^2 = G*m1*(y1 - y3)/beta + G*m2*(y2 - y3)/gamma
15
16 where G = gravitational constant = 6.6725985 X 10^(-11) N-m^2/kg^2
17 alpha = [ (x2 - x1)^2 + (y2 - y1)^2 ]^(3/2) AND alpha <> 0
18 beta = [ (x1 - x3)^2 + (y1 - y3)^2 ]^(3/2) AND beta <> 0
19 gamma = [ (x3 - x2)^2 + (y3 - y2)^2 ]^(3/2) AND gamma <> 0
20 */
21
22 var N = 3; // The number of bodies (point masses) this code is designed to handle.
23 var G = 6.67384E-11; // Big-G, in N(m/kg)^2.
24 var h = 0.000001; // Interval between time steps, in seconds. The smaller the value the more accurate the simulation. This value was empirically derived by visually observing the simulation over time.
25 var iterationsPerFrame = 400; // The number of calculations made per animation frame, this is an empirically derived number based on the value of h.
26
27 var m1;
28 var m1_half; // Initially, will contain a copy of m1.
29 var m2;
30 var m2_half;
31 var m3;
32 var m3_half;
33
34 self.onmessage = function (evt) { // evt.data contains the data passed from the calling main page thread.
35 switch (evt.data.cmd) {
36 case 'init':
37 init(evt.data.initialConditions); // Transfer the initial conditions data to the persistant variables in this thread.
38 break;
39 case 'crunch':
40 crunch();
41 break;
42 default:
43 console.error("ERROR FROM worker.js: SWITCH STATEMENT ERROR IN self.onmessage");
44 } // switch
45 };
46
47 // The denominators alpha, beta, and gamma for the acceleration equations 42 through 47:
48 function alpha(m1, m2) { // Equation 48.
49 var delta_x = m2.p.x - m1.p.x;
50 var delta_y = m2.p.y - m1.p.y;
51
52 var delta_x_squared = delta_x * delta_x;
53 var delta_y_squared = delta_y * delta_y;
54
55 var base = delta_x_squared + delta_y_squared;
56
57 return Math.sqrt(base * base * base); // Raise the base to the 3/2 power so as to calculate (x_2 - x_1 )^2 + (y_2 - y_1 )^2]^(3/2), equation 48.
58 }
59
60 function beta(m1, m3) { // Equation 49.
61 var delta_x = m3.p.x - m1.p.x;
62 var delta_y = m3.p.y - m1.p.y;
63
64 var delta_x_squared = delta_x * delta_x;
65 var delta_y_squared = delta_y * delta_y;
66
67 var base = delta_x_squared + delta_y_squared;
68
69 return Math.sqrt(base * base * base); // Raise the base to the 3/2 power so as to calculate (x3 - x1)^2 + (y3 - y1)^2 ]^(3/2), equation 49.
70 }
71
72 function gamma(m2, m3) { // Equation 50.
73 var delta_x = m3.p.x - m2.p.x;
74 var delta_y = m3.p.y - m2.p.y;
75
76 var delta_x_squared = delta_x * delta_x;
77 var delta_y_squared = delta_y * delta_y;
78
79 var base = delta_x_squared + delta_y_squared;
80
81 return Math.sqrt(base * base * base); // Raise the base to the 3/2 power so as to calculate (x3 - x2)^2 + (y3 - y2)^2]^(3/2), equation 50.
82 }
83
84 /*
85 Note that the alpha, beta, and gamma functions could be replaced with a single alpha_beta_gamma(massA, massB) function but for clarity, this was not done.
86 */
87
88 this.init = function (initialConditions) {
89
90 // Define local mass object constructor function:
91 function Mass(initialCondition) {
92 this.m = initialCondition.mass; // The mass of the point mass.
93 this.p = { x: initialCondition.position.x, y: initialCondition.position.y }; // The position of the mass.
94 this.v = { x: initialCondition.velocity.x, y: initialCondition.velocity.y }; // The x- and y-components of velocity for the mass.
95 this.a = {}; // Will contain the x- and y-components of acceleration for the mass.
96 }
97
98 if (initialConditions.length != N) {
99 console.error("ERROR FROM worker.js: THE initialConditions ARRAY DOES NOT CONTAIN EXACTLY " + N + " OBJECTS - init() TERMINATED");
100 return;
101 }
102
103 // Set the local mass object global variables:
104 m1 = new Mass(initialConditions[0]);
105 m1_half = new Mass(initialConditions[0]); // Create a copy of m1.
106 m2 = new Mass(initialConditions[1]);
107 m2_half = new Mass(initialConditions[1]);
108 m3 = new Mass(initialConditions[2]);
109 m3_half = new Mass(initialConditions[2]);
110
111 // Calculate initial acceleration values (using initial conditions) in preparation for using equation 25:
112 m1.a.x = G * m2.m * (m2.p.x - m1.p.x) / alpha(m1, m2) + G * m3.m * (m3.p.x - m1.p.x) / beta(m1, m3); // Equation 42.
113 m1.a.y = G * m2.m * (m2.p.y - m1.p.y) / alpha(m1, m2) + G * m3.m * (m3.p.y - m1.p.y) / beta(m1, m3); // Equation 43.
114 m2.a.x = G * m1.m * (m1.p.x - m2.p.x) / alpha(m1, m2) + G * m3.m * (m3.p.x - m2.p.x) / gamma(m2, m3); // Equation 44.
115 m2.a.y = G * m1.m * (m1.p.y - m2.p.y) / alpha(m1, m2) + G * m3.m * (m3.p.y - m2.p.y) / gamma(m2, m3); // Equation 45.
116 m3.a.x = G * m1.m * (m1.p.x - m3.p.x) / beta(m1, m3) + G * m2.m * (m2.p.x - m3.p.x) / gamma(m2, m3); // Equation 46.
117 m3.a.y = G * m1.m * (m1.p.y - m3.p.y) / beta(m1, m3) + G * m2.m * (m2.p.y - m3.p.y) / gamma(m2, m3); // Equation 47.
118
119 function equation25(x, v, a) {
120 return x + 0.5 * h * v + 0.25 * (h * h) * a; // Equation 25.
121 }
122
123 // For the first iteration (and only the first iteration), use equation 25 (instead of equation 22) to calculate the initial half-integer position values:
124 m1_half.p.x = equation25(m1.p.x, m1.v.x, m1.a.x);
125 m1_half.p.y = equation25(m1.p.y, m1.v.y, m1.a.y);
126 m2_half.p.x = equation25(m2.p.x, m2.v.x, m2.a.x);
127 m2_half.p.y = equation25(m2.p.y, m2.v.y, m2.a.y);
128 m3_half.p.x = equation25(m3.p.x, m3.v.x, m3.a.x);
129 m3_half.p.y = equation25(m3.p.y, m3.v.y, m3.a.y);
130 } // this.init
131
132
133 this.crunch = function () {
134 for (var i = 0; i < iterationsPerFrame; i++) {
135 // Calculate half-integer acceleration values (using equations 18 through 21) in preparation for using equation 23:
136 m1_half.a.x = G * m2_half.m * (m2_half.p.x - m1_half.p.x) / alpha(m1_half, m2_half) + G * m3_half.m * (m3_half.p.x - m1_half.p.x) / beta(m1_half, m3_half); // Equation 42.
137 m1_half.a.y = G * m2_half.m * (m2_half.p.y - m1_half.p.y) / alpha(m1_half, m2_half) + G * m3_half.m * (m3_half.p.y - m1_half.p.y) / beta(m1_half, m3_half); // Equation 43.
138 m2_half.a.x = G * m1_half.m * (m1_half.p.x - m2_half.p.x) / alpha(m1_half, m2_half) + G * m3_half.m * (m3_half.p.x - m2_half.p.x) / gamma(m2_half, m3_half); // Equation 44.
139 m2_half.a.y = G * m1_half.m * (m1_half.p.y - m2_half.p.y) / alpha(m1_half, m2_half) + G * m3_half.m * (m3_half.p.y - m2_half.p.y) / gamma(m2_half, m3_half); // Equation 45.
140 m3_half.a.x = G * m1_half.m * (m1_half.p.x - m3_half.p.x) / beta(m1_half, m3_half) + G * m2_half.m * (m2_half.p.x - m3_half.p.x) / gamma(m2_half, m3_half); // Equation 46.
141 m3_half.a.y = G * m1_half.m * (m1_half.p.y - m3_half.p.y) / beta(m1_half, m3_half) + G * m2_half.m * (m2_half.p.y - m3_half.p.y) / gamma(m2_half, m3_half); // Equation 47.
142
143 // Calculate velocity values using equation 23:
144 m1.v.x = equation23(m1.v.x, m1_half.a.x);
145 m1.v.y = equation23(m1.v.y, m1_half.a.y);
146 m2.v.x = equation23(m2.v.x, m2_half.a.x);
147 m2.v.y = equation23(m2.v.y, m2_half.a.y);
148 m3.v.x = equation23(m3.v.x, m3_half.a.x);
149 m3.v.y = equation23(m3.v.y, m3_half.a.y);
150
151 // Calculate position values using equation 24:
152 m1.p.x = equation24(m1_half.p.x, m1.v.x);
153 m1.p.y = equation24(m1_half.p.y, m1.v.y);
154 m2.p.x = equation24(m2_half.p.x, m2.v.x);
155 m2.p.y = equation24(m2_half.p.y, m2.v.y);
156 m3.p.x = equation24(m3_half.p.x, m3.v.x);
157 m3.p.y = equation24(m3_half.p.y, m3.v.y);
158
159 // Calculate half-integer position values using equation 22:
160 m1_half.p.x = equation22(m1.p.x, m1.v.x);
161 m1_half.p.y = equation22(m1.p.y, m1.v.y);
162 m2_half.p.x = equation22(m2.p.x, m2.v.x);
163 m2_half.p.y = equation22(m2.p.y, m2.v.y);
164 m3_half.p.x = equation22(m3.p.x, m3.v.x);
165 m3_half.p.y = equation22(m3.p.y, m3.v.y);
166 } // for
167 //////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
168 self.postMessage([m1/*, m2, m3*/]); // Send the crunched data back to the UI thread to be rendered onscreen.
169 //////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
170 function equation23(v, a) {
171 return v + h * a; // Equation 23.
172 }
173
174 function equation24(x, v) {
175 return x + 0.5 * h * v; // Equation 24.
176 }
177
178 function equation22(x, v) {
179 return x + 0.5 * h * v; // Equation 22, this function is of course the same as the equation24(x, v) function.
180 }
181 } // this.crunch
В случае трех материальных тел на каждое из них действуют две силы со стороны двух других тел. Например, на тело m₁ действуют следующие силы (F₂ и F₃):
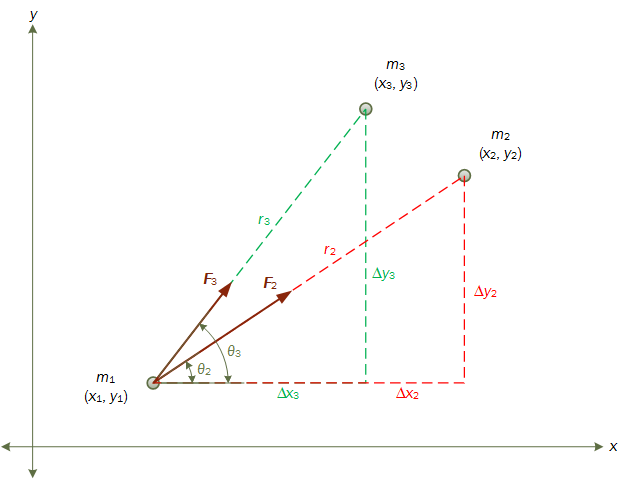
Сначала заметим, что результирующая сила F₁, действующая на тело m₁, будет суммой сил F₂ и F₃. Это значит, что F₁ = m₁a₁ = F₂ + F₃.
Теперь по тригонометрическим законам, мы можем разложить модуль результирующей силы F₁, действующей на тело m₁, на компоненты x и y:

В красном и зеленом треугольниках на рис. мы видим:
Согласно закону всемирного тяготения Ньютона, F₂ и F₃ можно выразить как:

Подставляя формулы, получим:
Эту систему уравнений (34,35,38-41) можно решить численно методом интегрирования "чехарда" (формулы 22–24) по заданным начальным условиям (значения массы, положения и скорости для каждого тела) с приемлемой точностью и стабильностью. Чтобы быстро добиться высокой точности, можно использовать рабочий веб-процесс для выполнения численного интегрирования в потоке, отдельном от потока пользовательского интерфейса главной страницы.
Рассмотрим N небесных тел. Пусть i обозначает одно из тел (i = 1, …, N), а h — малый интервал времени. В позиционном алгоритме Верле следующие значения положения и скорости тела i вычисляются следующим образом:

номера возле формул соответствуют номерам формул в программе(см.текст программы K3.js)
firekeepers casino <a href="https://onlinecasinodd.com/">zone online casino games</a> free slots games <a href="https://onlinecasinodd.com/">online casino gambling</a> | https://onlinecasinodd.com/ - free online casino https://onlinecasinodd.com/ - firekeepers casino
Ссылки по теме[править]
- Физические законы и формулы для задачи двух и трех тел.
- Овалы Кассини и лемниската- Курс высшей математики, Т.1
- «Гравитация» А. Н. Петров