КП: Движение спутника в двойной системе — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
(→Общие сведения по теме) |
(→Общие сведения по теме) |
||
| Строка 18: | Строка 18: | ||
Задачи подобного рода решаются с помощью уравнения Лагранжа 2-ого рода: | Задачи подобного рода решаются с помощью уравнения Лагранжа 2-ого рода: | ||
| − | [[Файл:Lagrange.png|thumbnail]] | + | [[Файл:Lagrange.png|thumbnail|200px|thumb|left]] |
| − | ,где [[Файл:L.png|thumbnail]]- функция Лагранжа (лагранжиан),[[Файл:Q.png| | + | ,где [[Файл:L.png|thumbnail|200px|thumb|left]]- функция Лагранжа (лагранжиан),[[Файл:Q.png|thumbnai|200px|thumb|leftl]]- обобщенная координата, t — время, |
i— число степеней свободы механической системы | i— число степеней свободы механической системы | ||
Версия 16:29, 7 апреля 2015
А.М. Кривцов > Теоретическая механика > Курсовые проекты ТМ 2015 > Движение спутника в двойной системе
Курсовой проект по Теоретической механике
Исполнитель: Мущак Никита
Группа: 09 (23604)
Семестр: весна 2015
Содержание
Формулировка задачи
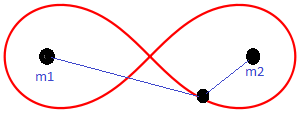
Исследовать движение спутника двойной системы. Двойная система состоит из 2 неподвижных планет. Определить устойчивость такого движения, а также его траекторию.
Общие сведения по теме
Задачи подобного рода решаются с помощью уравнения Лагранжа 2-ого рода:
,гдеФайл:L.png
thumb
Файл:Q.png
leftl
i— число степеней свободы механической системы
Лагранжиан будем считать как разность кинетической и потенциальной энергий системы.
Дальнейшим интегрированием получаем уравнение движения.
Решение
Обсуждение результатов и выводы
Скачать отчет:
Скачать презентацию: