Курсовые работы по ТОМДЧ: 2012-2013 — различия между версиями

Версия 17:44, 24 января 2013

Общие сведения

Предмет: "Теоретические основы метода динамики частиц"

Лектор: Виталий Андреевич Кузькин

Группа: 40510

Учебный год: 2012-2013

Семестр: осень 2012

Моделирование кручения стержня квадратного сечения

Исполнители: Чебышев Игорь

Начальные условия:

Крайние сечения ( 2 ряда ) поворачиваем на угол [math]\alpha = 0,005/-0,005 [/math] радиан относительно оси симметрии, которая проходит вдоль стержня.

Для поворота сечения используются следующие формулы:

[math]Y = y Cos(\alpha) - x Sin (\alpha)[/math]

[math]X = y Sin (\alpha) + x Cos(\alpha)[/math]

Размеры стержня в частицах:

[math]X=200[/math]

[math]Y=Z=25[/math]

Всего частиц [math]125000[/math]

Моделирование деформирования прямоугольной пластины под действием силы на группу частиц

‎

Исполнители: Цветков Денис

Рассматривается пластина, закрепленная сверху, под действием некоторой силы, действующей на нижнюю часть пластины.

Для описания взаимодействия между частицами использовался потенциал Леннард-Джонса. На каждую частицу действует объемная сила, имитирующая гравитационные силы.

Сила воздействует на тело в течении ~1/8 периода колебания пластины.

Моделирование течения двухфазной жидкости

Исполнители: Буковская Карина

Рассматривается установившееся течение несжимаемой жидкости с постоянной вязкостью в тонкой цилиндрической трубке круглого сечения под действием постоянной разности давлений. Если предположить, что течение будет ламинарным и одномерным, то уравнение решается аналитически, и для скорости получается параболический профиль (часто называемый профилем Пуазейля) — распределение скорости в зависимости от расстояния до оси канала

                v=(ρ_1-ρ_1)/4μl(1-r^2)

v — скорость жидкости вдоль трубопровода, м/с;r — расстояние от оси трубопровода, м;p1 − p2 — разность давлений на входе и на выходе из трубы, Па;μ — вязкость жидкости, Н•с/м²;l — длина трубы, м. Закон Хагена — Пуазейля, определяющий расход жидкости при установившемся течении вязкой несжимаемой жидкости в тонкой цилиндрической трубе круглого сечения.

               Q=(π∙d^4∙(ρ_(1-) ρ_2))/(128∙μ∙l)=(π∙r^4∙(ρ_(1-) ρ_2))/(8∙μ∙l)

Q — расход жидкости в трубопроводе, м³/с;d — диаметр трубопровода, м;r — радиус трубопровода, м;p1 − p2 — разность давлений на входе и на выходе из трубы, Па;μ — вязкость жидкости, Н•с/м²;l — длина трубы, м.

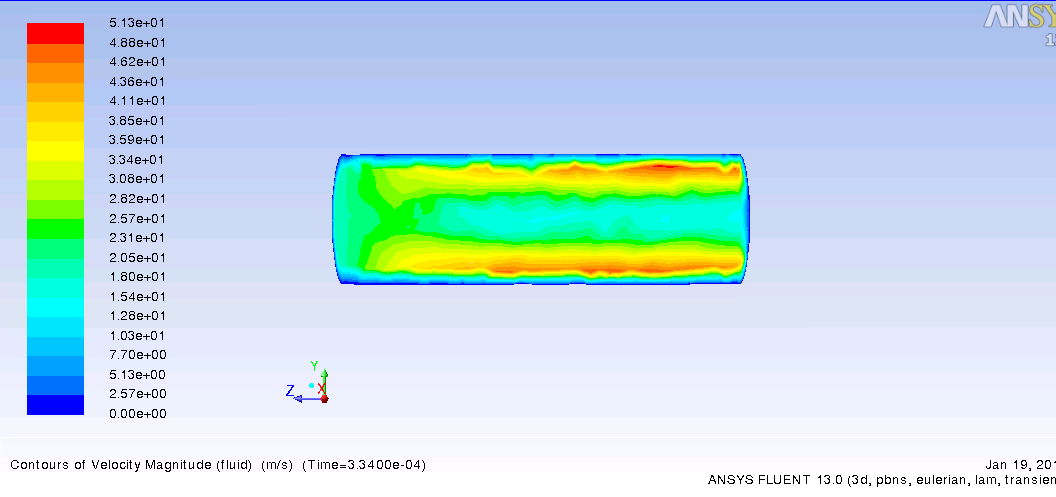-график показателей скорости 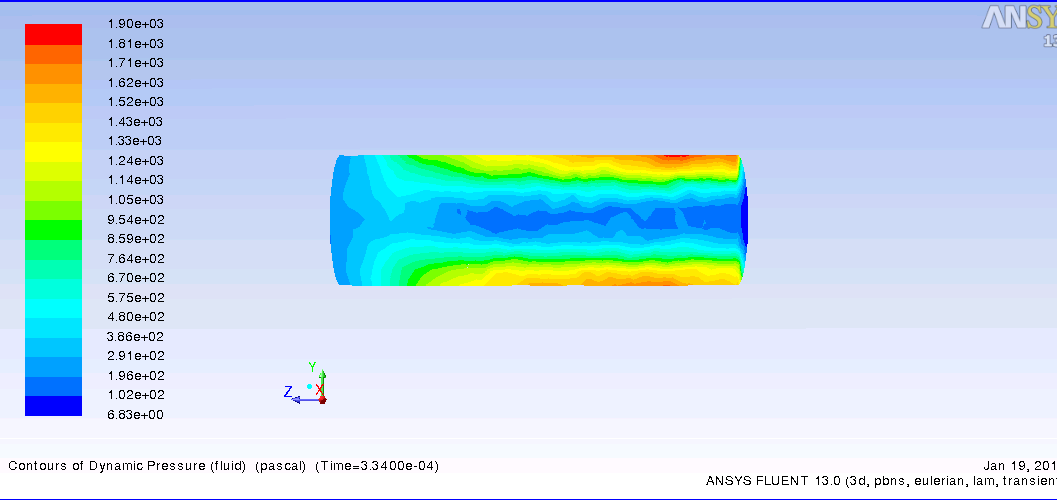-график показателей давления

Моделирование продольного изгиба стержня. Потеря устойчивости под действием осевой силы

Исполнители: Дмитрий Ершов

рис. 1‎

В рассмотрении находится тонкий стержень, который покоится в начальный момент времени. На стержень начинает действовать постоянная продольная сжимающая сила P с разных концов стержня. Схема нагружения на рис.1. Необходимо проанализировать поведение стержня под действием сжимающей силы. Определить, при каком значении силы (критическая сила) будет происходить потеря устойчивости.

• 

  r=0.01‎

• 

  ‎r=0.005

• 

  r=0.003‎

• 

  r=0.001

• 

  r=0.0005‎

• 

  r=0.0001‎

Для описания взаимодействия между частицами использовался метод молекулярной динамики. Сила задается через перемещения концов стержя Стержень состоит из 800 частиц (400x2x2).

См. также

• Метод динамики частиц
• Механика дискретных сред
• Теоретические_основы_метода_динамики_частиц
• Курсовые работы 2011-2012 учебного года