Сравнение методов интегрирования уравнений динамики цепочки — различия между версиями
Pepper (обсуждение | вклад) (→Численное решение) |
Loban9614 (обсуждение | вклад) (→Численное решение) |
||
| Строка 28: | Строка 28: | ||
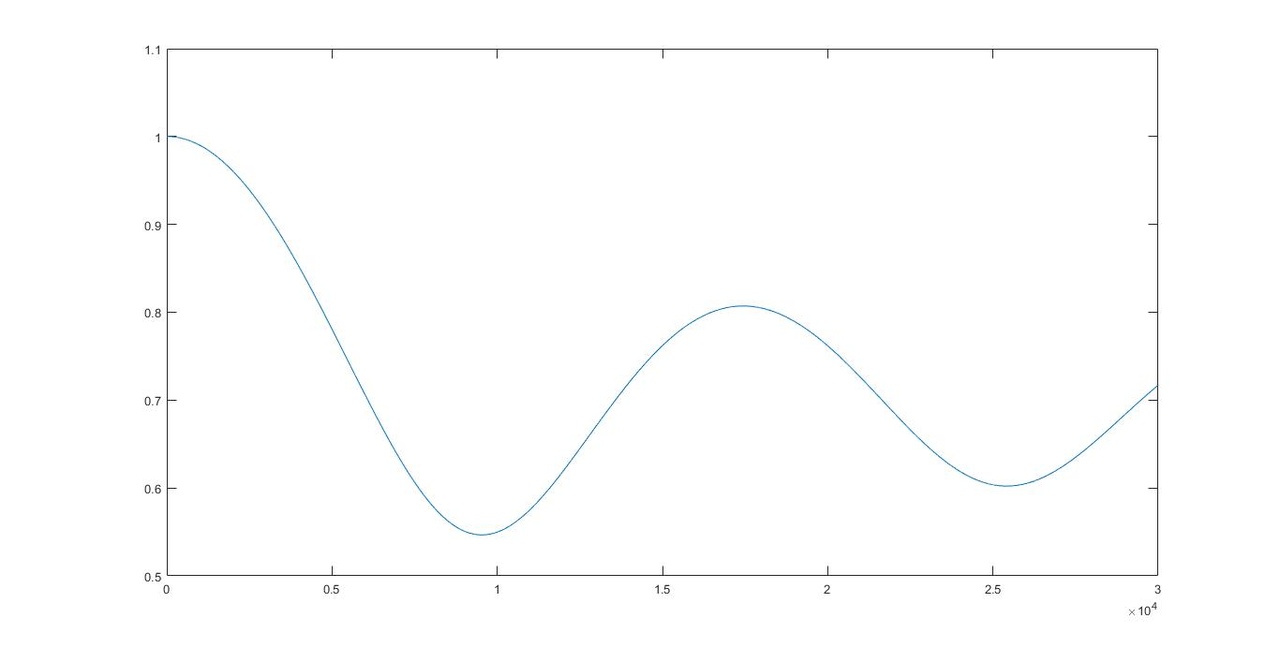
Численное решение для 100 частиц методом Рунге-Кутта 4 порядка | Численное решение для 100 частиц методом Рунге-Кутта 4 порядка | ||
[[File:uD5csQmC_F4.jpg|center]] | [[File:uD5csQmC_F4.jpg|center]] | ||
| + | [[File:UD5csQmC F4|thumb]] | ||
Версия 00:18, 23 января 2019
Постановка задачи
Рассматривается цепочка элементов, состоящая из одинаковых масс m. Термин одномерная цепочка означает в дальнейшем совокупность расположенных вдоль прямой линии N материальных частиц P0, P1, ... Pn, ..., PN–1. Рассматриваются продольные колебания образующих цепочку частиц под действием сил взаимодействия между частицами цепочки, а также параллельных направлению цепочки внешних сил. Движение частицы с номером n описывается зависимостью от времени t её смещения un относительно положения равновесия этой частицы (узла цепочки с номером n).
Решение
Рассмотрим модель колебаний одномерной многоатомной цепочки равных масс. Пусть в этой цепочке находится N атомов. Обозначим смещение n-го атома un, а атома, отстоящего от него на p узлов, – un+p. Примем в качестве положительных смещения атомов вправо от положения равновесия, а отрицательных – влево.
Каждый атом смещается только вдоль цепочки, что следует из требования одномерности модели. Пусть атомы связаны между собой упругой силой F с коэффициентом упругости с. Найдем уравнение движения n-го и n+1-го атома в цепи. В равновесном положении силы, действующие на атомы, равны нулю. При произвольных смещениях на каждый n-й атом будет действовать сила со стороны соседних атомов. В соответствии с элементарным законом Гука эту силу можно представить в виде:
В качестве начальных условий заданы случайные начальные скорости таким образом, что средняя скорость всех частиц равна 0. Перемещения всех частиц в начальный момент времени равны нулю. Также заданы периодические граничные условия на перемещения.
Методы Верле, Эйлера и Рунге-Кутта
Метод Эйлера - простейший численный метод решения систем обыкновенных дифференциальных уравнений. Метод Эйлера является явным, одношаговым методом первого порядка точности. Он основан на аппроксимации интегральной кривой кусочно-линейной функцией, так называемой ломаной Эйлера.
Наиболее часто используется и реализован в различных математических пакетах классический метод Рунге — Кутты, имеющий четвёртый порядок точности. При выполнении расчётов с повышенной точностью всё чаще применяются методы пятого и шестого порядков точности. Построение схем более высокого порядка сопряжено с большими вычислительными трудностями.
Среди наиболее известных методов интегрирования уравнений движения можно выделить алгоритм Верле. Рассмотрим построение алгоритма Верле, для простоты, в одномерном виде. Основная идея алгоритма Верле состоит в записи разложения положения частицы.
Численное решение
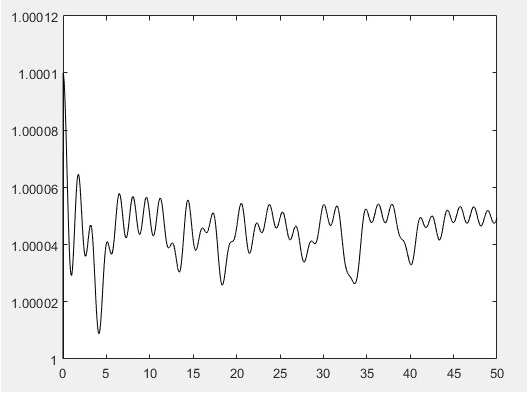
Численное решение для 100 частиц методом Верле
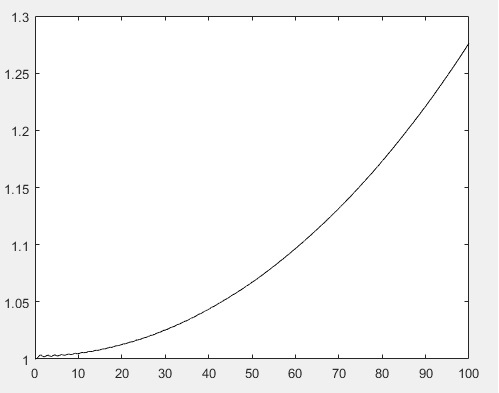
Численное решение для 100 частиц методом Эйлера
Численное решение для 100 частиц методом Рунге-Кутта 4 порядка