Сравнение методов интегрирования уравнений динамики цепочки

Курсовые работы 2018-2019 учебного года > Сравнение методов интегрирования уравнений динамики цепочки

---

Курсовой проект по Механике дискретных сред

Исполнитель: Иванова Яна

Группа: 43604/1

Семестр: осень 2018

Постановка задачи

Рассматривается одномерная цепочка элементов, состоящая из частиц с одинаковыми массами m. Термин "одномерная цепочка" означает совокупность расположенных вдоль прямой линии N материальных частиц.. Рассматриваются продольные колебания образующих цепочку частиц под действием сил взаимодействия между частицами цепочки. Движение частицы с номером n описывается зависимостью от времени t её смещения относительно положения равновесия этой частицы (узла цепочки с номером n). Примем в качестве положительных смещения атомов вправо от положения равновесия, а отрицательных – влево. Каждый атом смещается только вдоль цепочки, что следует из требования одномерности модели. Такие смещения характерны для продольной волны.

Решение

Каждый атом смещается только вдоль цепочки, что следует из требования одномерности модели. Пусть атомы связаны между собой упругой силой F с коэффициентом упругости с. Найдем уравнение движения n-го и n+1-го атома в цепи. В равновесном положении силы, действующие на атомы, равны нулю. При произвольных смещениях на каждый n-й атом будет действовать сила со стороны соседних атомов. Уравнение движения имеет вид:

[math] {m}\ddot{\bf U}_{i} = {С}({\bf U}_{i-1}-2{\bf U}_{i} + {\bf U}_{i+1}), [/math]

где С - жёсткость одной пружинки, m - масса одной частицы, [math] {\bf U}_{i} [/math] - перемещение частицы, a - расстояние между двумя соседними частицами в начальный момент времени.

Период одного колебания:[math] {T}_{o} = 2{\pi}\sqrt\frac {m}{C} [/math] В качестве начальных условий заданы случайные начальные скорости рандомным образом. Перемещения всех частиц в начальный момент времени равны нулю. Полная энергия системы складывается из потенциальной энергии взаимодействия частиц и их кинетической энергии в каждый момент времени. В циклах для потенциальной и кинетической энергий рассчитываются эти значения. Далее производится нормировка, энергии складываются и строится график зависимости.

Методы Верле, Эйлера и Рунге-Кутта

Метод Эйлера - простейший численный метод решения систем обыкновенных дифференциальных уравнений. Метод Эйлера является явным, одношаговым методом первого порядка точности. Он основан на аппроксимации интегральной кривой кусочно-линейной функцией, так называемой ломаной Эйлера.

Наиболее часто используется и реализован в различных математических пакетах классический метод Рунге — Кутты, имеющий четвёртый порядок точности. При выполнении расчётов с повышенной точностью всё чаще применяются методы пятого и шестого порядков точности. Построение схем более высокого порядка сопряжено с большими вычислительными трудностями.

Среди наиболее известных методов интегрирования уравнений движения можно выделить алгоритм Верле. Рассмотрим построение алгоритма Верле, для простоты, в одномерном виде. Основная идея алгоритма Верле состоит в записи разложения положения частицы.

Численное решение

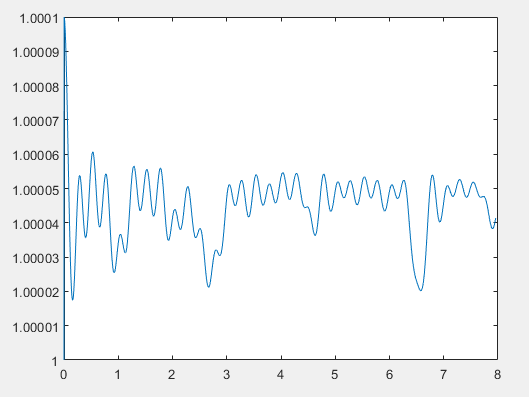
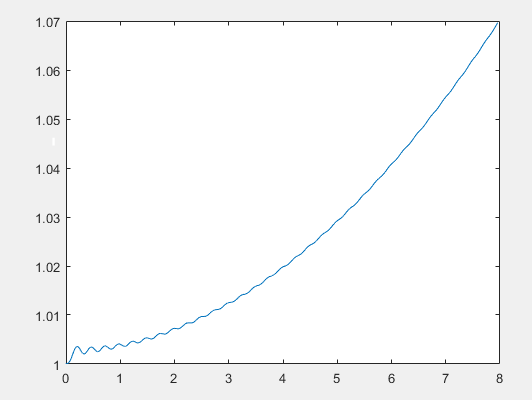
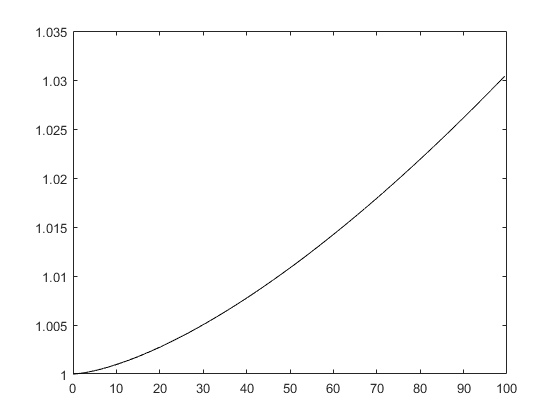
Построим графики зависимости безразмерной энергии от безразмерного времени для 100000 частиц с шагом по времени dt = 0.01 и 5000 шагов интегрирования. По оси абсцисс откладывается время, отнесенное к периоду, по оси ординат - энергия, отнесенное к начальной энергии системы.

Численное решение методом Верле

Численное решение методом Эйлера

Численное решение методом Рунге-Кутта 4 порядка

Результаты

Метод Верле является симплектическим, то есть сохраняющим энергию с течением времени. Это можно проследить из графика, безразмерная энергия колеблется в пределах единицы. Методы Эйлера и Рунге-Кутта 4 порядка энергию не сохраняют, что заметно из возрастания графиков.