КП: Штрафной удар по воротам — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
(→‎Решение)
(→‎Решение)
Строка 93: Строка 93:
 
<big><math>
 
<big><math>
 
\begin{cases}
 
\begin{cases}
−
v_x^{i+1} = v_x^i + (-6πrηv_x^i/m + 8πρr^3(u_z^iω_z - u_y^iω_z)/m)\Delta t  \\
+
v_x^{i+1} = v_x^i + (-6πrηv_x^i/m + 8πρr^3(u_z^iω_y - u_y^iω_z)/m)\Delta t  \\
−
v_y^{i+1} = v_y^i + (-6πrηv_y^i/m + 8πρr^3(u_x^iω_w - u_z^iω_x)/m)\Delta t  \\
+
v_y^{i+1} = v_y^i + (-6πrηv_y^i/m + 8πρr^3(u_x^iω_z - u_z^iω_x)/m)\Delta t  \\
−
v_z^{i+1} = v_z^i + (-g-6πrηv_z^i/m + 8πρr^3(u_y^iω_y - u_x^iω_y)/m)\Delta t  \\
+
v_z^{i+1} = v_z^i + (-g-6πrηv_z^i/m + 8πρr^3(u_y^iω_x - u_x^iω_y)/m)\Delta t  \\
 
\end{cases}
 
\end{cases}
 
</math></big>
 
</math></big>

Версия 18:50, 2 июня 2015

А.М. Кривцов > Теоретическая механика > Курсовые проекты ТМ 2015 > Штрафной удар по воротам


Курсовой проект по Теоретической механике

Исполнитель: Филимонов Александр

Группа: 09 (23604)

Семестр: весна 2015

Штрайной удар Роберто Карлоса

Аннотация проекта

Данный проект посвящен изучению динамики движения футбольного мяча во время штрафного удара. В ходе работы над проектом был рассмотрен конкретный штрафной удар, который был исполнен Роберто Карлосом в товарищеском матче Бразилия - Франция. Этот удар был симулирован на языке JavaScript.

Формулировка задачи

  • Написать программу, которая моделирует процесс движения футбольного мяча во время штрафного удара, с учетом внешних сил и воздействий.

Общие сведения по теме

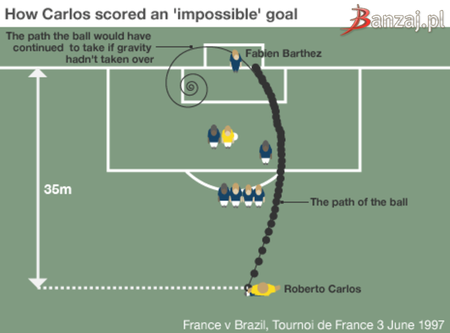
Роберто Карлос забил в 1997 году в ворота сборной Франции невероятный по красоте гол.

Мяч был установлен примерно в 30 - 35 м от ворот соперников, ближе к правому краю поля. После удара Карлоса мяч полетел далеко в правую сторону, облетел «стенку» в метре от нее и после этого чудесным образом мяч повернул влево и влетел в ворота - к изумлению игроков, вратаря и представителей СМИ.

Этот удар стал наглядным примером силы Магнуса, действующей на тело, движущееся с вращением при обтекании его потоком жидкости или газа.

Траектория движения мяча во время штрафного удара


Входные данные

  • На основании статьи, посвященной удару Роберто Карлоса можно вычленить входные данные для нашей программы и посмотреть на полученную в программе траекторию.

- [math] v_{0} = 35 (м/с) [/math] - начальная скорость мяча;

- [math] d = 35 (м) [/math] - расстояние от мяча до ворот;

- [math] \omega_{z} = 10 (об/с) =62.8 (рад/с)[/math] - скорость вращения мяча во время полета;

- Также было известно, что погода была сухая и безветренная, то есть скорость ветра по всем осям равна 0.

Решение

[math]\vec{F_{р}} = \vec{F_{тяж}} + \vec{F_{сопр}} + \vec{F_{м}} [/math], где

[math] \vec{F_{р}} [/math] - Равнодействующая сил на мяч;

[math] \vec{F_{тяж}} [/math] - Сила тяжести, действующая на мяч;

[math] \vec{F_{сопр}} [/math] - Сила сопротивления воздуха;

[math] \vec{F_{м}} [/math] - Сила Магнуса.


Сила тяжести:

[math] \vec{F_{тяж}} = m\vec{g} [/math], где

[math] m [/math] - масса мяча;

[math] g [/math] - ускорение свободного падения.


Силу сопротивления воздуха будем считать с помощью закона Стокса:

[math]\vec{F} = -6πrη\vec{v} [/math] , где

[math]\vec{F}[/math] - сила Стокса,

[math]r[/math] - радиус мяча,

[math]η[/math] - динамическая вязкость,

[math]\vec{v}[/math] - скорость мяча.


Силу Магнуса примем вида:

[math]\vec{F} = 8πρr^3\vec{u}\times\vec{ω} [/math] , где

[math]\vec{F}[/math] - сила Магнуса,

[math]ρ[/math] - плотность воздуха,

[math]r[/math] - радиус мяча,

[math]\vec{u}[/math] - относительная скорость мяча,

[math]\vec{ω}[/math] - угловая скорость мяча.

Применив метод Эйлера, получим формулы для нахождения скорости и координаты мяча:

[math] \begin{cases} v_x^{i+1} = v_x^i + (-6πrηv_x^i/m + 8πρr^3(u_z^iω_y - u_y^iω_z)/m)\Delta t \\ v_y^{i+1} = v_y^i + (-6πrηv_y^i/m + 8πρr^3(u_x^iω_z - u_z^iω_x)/m)\Delta t \\ v_z^{i+1} = v_z^i + (-g-6πrηv_z^i/m + 8πρr^3(u_y^iω_x - u_x^iω_y)/m)\Delta t \\ \end{cases} [/math]

[math] \begin{cases} x^{i+1} = x^i + v_x^i\Delta t \\ y^{i+1} = y^i + v_y^i\Delta t \\ z^{i+1} = z^i + v_z^i\Delta t \\ \end{cases} [/math];

Обсуждение результатов и выводы

  • Таким образом, в ходе работы над проектом была написана программа, моделирующая траекторию движения мяча во время штрафного удара, а так же смоделирован конкретный удар, при известных условиях.
  • Подставив в программу данные, полученные учеными, можно увидеть как мяч залетает в ворота.


Скачать отчет:
Скачать презентацию:

Ссылки по теме

См. также

Источник — «http://tm.spbstu.ru/?title=КП:_Штрафной_удар_по_воротам&oldid=34251»