Курсовые работы по ТОМДЧ: 2013-2014 — различия между версиями

Версия 12:40, 23 января 2014

Предмет: "Теоретические основы метода динамики частиц"

Лектор: Виталий Андреевич Кузькин

Группа: 40510

Учебный год: 2013-2014

Семестр: осень 2013

Моделирование распространения поперечных волн в двумерном стрежне

Исполнители:: Степанов Алексей

Рассматривается стержень, имеющий толщину в 1 атом. Взаимодействие между атомами, находящимися на расстоянии меньшем, чем радиус обрезания, описывается законом

[math] \underline{F}(r) = k \frac{\left|\underline{r}\right|-a_{0}}{\left|\underline{r}\right|}\underline{r} [/math]

Здесь, [math]k[/math] — жесткость связи, [math]\underline{r}[/math] — радиус-вектор, соединяющий частицы и [math]a_{0}[/math] равновесное расстояние. Радиус обрезания в работе выбран: [math] r_{cut} = 1.5 [/math].

Было смоделировано несколько различных задач:

• Отражение волны от свободного конца
• Отражение волны от заделанного конца
• Распространение волны без дисперсии
• Распространение волны с дисперсией

Во всех этих задачах, граничный условия на другом конце выглядели так:

[math] \begin{cases} y(t) = A\sin\left(\frac{2\pi t}{T}\right), t \lt \frac{T}{2}\\ F = 0, t \gt \frac{T}{2} \end{cases} [/math]

Результаты:

• Отражение волны от свободного конца

• Отражение волны от заделанного конца

• Распространение волны с дисперсией
• Соударение двух встречных волн

Моделирование цепочки частиц, анализ распределения скоростей

Исполнители: Дзенушко Дайнис

Рассматривается цепочка частиц с периодичными граничными условиями. Задаются начальные скорости частиц, т.е. вводится начальная температура.
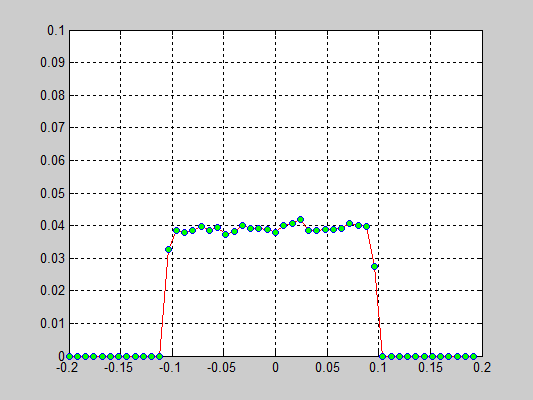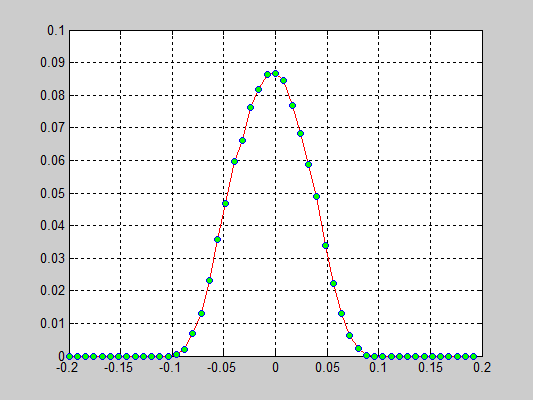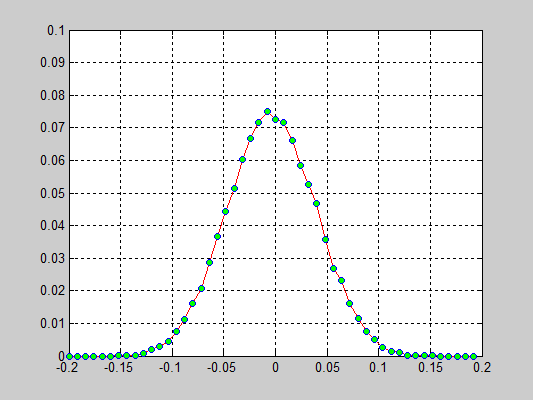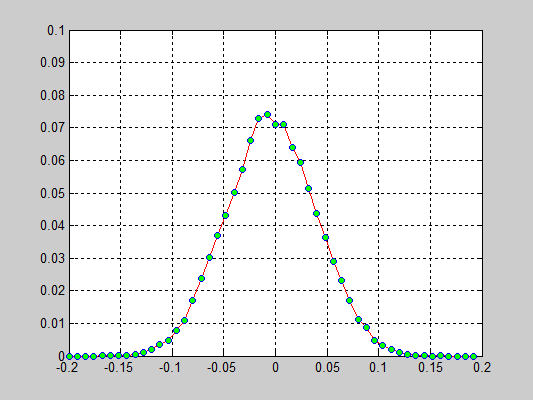
Исследуется распределение скоростей частиц от времени. В начальной конфигурации задается равномерное распределение скоростей.

Взаимодействие частиц описывается потенциалом Леннарда-Джонса который записывается в следующем виде:
[math]U(r) = D \left[ \left(\frac{a}{r}\right)^{12} - \left(\frac{a}{r}\right)^{6} \right],[/math]
r — расстояние между центрами частиц
D  — глубина потенциальной ямы
a — равновесное расстояние

Результаты:

• 20000 частиц, без диссипаций, радиус обрезания a_cut = 1.4 a0, максимальные начальные скорости v0 = 0.5 * vo / 6
  

• 20000 частиц, с диссипацией B = 2.6 * Bo / 100, радиус обрезания a_cut = 1.4 a0, максимальные начальные скорости v0 = 0.5 * vo / 6
  

(Посмотреть результат)

См. также

• Метод динамики частиц
• Механика дискретных сред
• Теоретические_основы_метода_динамики_частиц
• Курсовые работы 2011-2012 учебного года