V-model — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
(→‎Advantages of V-model)
(→‎Introduction)
Строка 8: Строка 8:
  
  
−
Discrete Element Method (DEM) is widely used for computer simulation of granular materials both solid and free-flowing. In powders and other free-flowing media interactions between particles usually include contact forces, dry and viscous friction, cohesion, electrostatic forces etc. For simulation of solids particles are additionally connected by so-called bonds <ref name="BPM"/>, <ref name="Wang"/>. In general case bond transmits both forces and moments acting between particles. They are responsible for stability,  elasticity, strength and other intrinsic  properties that distinguish solids from free-flowing materials. The bonds may have different physical meaning. On the one hand they can specify the law of interaction between different parts of one material represented by the particles. On the other hand  bonds can be considered as a model of some additional glue-like or cement-like material, connecting particles.
+
The Discrete (or Distinct) Element Method (DEM) is widely used for the computer simulation of solid and free-flowing granular materials. Similarly to classical molecular dynamics, in the framework of DEM the material is represented by a set of many interacting rigid body particles (granules). The equations of the particles' motion are integrated numerically. In free-flowing materials the  particles interact via contact forces, dry and viscous friction forces, electrostatic forces, etc. Computer simulation of deformation and fracture of granular solids, such as rocks,  concrete, ceramics, particle compounds, agglomerates, nanocomposites, etc. is even more challenging. Particles in granular solids are usually connected together by some additional bonding material such as cement or glue. The example of composite material consisting of PbS nanoparticles bonded together by a copolymer is shown in figure above. The copolymer (bonding material) resists the relative translation and rotation of neighboring PbS particles. In DEM simulations bonding material is usually taken into account implicitly using the concept of so-called bonds. Neighboring particles are connected by the bonds that resist to stretching/compression, shear, bending, and torsion. The bonds cause forces and torques acting on the particles along with contact forces. Mass of the bonding material is usually neglected. The assumption does not influence static properties of the granular material. The influence on the dynamic properties is not so straightforward and should be considered separately. However let us note that in many practical applications the mass of bonding material is much smaller than the mass of the particles (see, for example, figures below). Therefore the mass of bonding
−
 
+
material can be neglected.
−
In practice models allowing to represent forces and moments, acting between particles, as a function of  characteristics of particle motion (linear and angular velocities, rotational matrixes, quaternions, etc.) are required. According to the review presented in paper <ref name="Wang"/> only several models presented in literature describe all possible kinds of deformation of the bond. Bonded-particle model (BPM) was proposed in paper <ref name="BPM"/> for simulation of rocks. The BPM model is widely used in literature for simulation of deformation and fracture of solids in both two and three dimensions. Several drawbacks of BPM model, in particular, in the case of coexistence of bending and torsion of the bond, are discussed in paper <ref name="Wang"/>. It is noted that the main reason for the drawbacks is incremental algorithm used in the framework of BPM model. Another approach based on decomposition of relative rotation of particles is proposed in paper <ref name="Wang"/>. Forces and moments are represented as functions of angles describing relative turn of the particles.
 
−
It was shown that method <ref name="Wang"/> is more accurate than incremental procedure of BPM model. However in the framework of model <ref name="Wang"/> potential energy of the bond and its relation to forces and torques are not considered. Though the expression for  potential energy is not required for DEM simulations it is still very important. It is required for control of energy conservation and construction of nonlinear elastic force laws. The approach proposed in paper <ref name="Wang"/> does not guarantee that the forces and moments caused by the bond are conservative. Note that any model for an elastic bond should be perfectly conservative.  
 
−
 
 
−
Also let us note the model  recently development by [http://www.dem-solutions.com/academic/edem-academic-workshop-proceedings.php  DEM-sloutions Ltd.]. It was proposed to use Timoshenko beam as a model of the bond connecting particle. Though the model has clear physical meaning it is also not the panacea. In particular, it is not straightforward how to implement this model in the case of finite rotations of the particles.  
 
−
 
 
−
There are also some other physical drawbacks of the existing bond models that are highlighted in the paper.
 
  
 
{|align="center"
 
{|align="center"
Строка 24: Строка 18:
 
  |}
 
  |}
  
 +
In the paper V.A. Kuzkin and I.E. Asonov "Vector-based model of elastic bonds for simulation of granullar solids"// Phys. Rev. E, 86, 051301, 2012  vector-based model(the V-model) of elastic bonds in solids is developed. Equations describing interactions between two rigid bodies in the general case are summarized. The general expression for the potential energy of the bond is represented  via vectors rigidly connected with bonded particles. The vectors are used for description of different types of bond's deformation. The expression for potential energy corresponding to tension/compression, shear, bending, and torsion of the bond is proposed. Forces and torques acting between particles are derived from the potential energy.
 +
Two approaches for calibration of V-model parameters for bonds with different length/thickness ratios are presented. Simple analytical formulas connecting geometrical and elastic characteristics of the bond with parameters of the V-model are derived. Main aspects of numerical implementation of the model are discussed.
  
 
== V-model ==
 
== V-model ==

Версия 16:15, 26 октября 2013

SEM image of composite consisting of nanoparticles bonded by a copolymer. (N. Preda, et. al., Mater. Res. Bull. 45, 1008 (2010))

Introduction

The article is based on the paper V.A. Kuzkin and I.E. Asonov "Vector-based model of elastic bonds for simulation of granullar solids"// Phys. Rev. E, 86, 051301, 2012. Author's copy can be downloaded here.


The Discrete (or Distinct) Element Method (DEM) is widely used for the computer simulation of solid and free-flowing granular materials. Similarly to classical molecular dynamics, in the framework of DEM the material is represented by a set of many interacting rigid body particles (granules). The equations of the particles' motion are integrated numerically. In free-flowing materials the particles interact via contact forces, dry and viscous friction forces, electrostatic forces, etc. Computer simulation of deformation and fracture of granular solids, such as rocks, concrete, ceramics, particle compounds, agglomerates, nanocomposites, etc. is even more challenging. Particles in granular solids are usually connected together by some additional bonding material such as cement or glue. The example of composite material consisting of PbS nanoparticles bonded together by a copolymer is shown in figure above. The copolymer (bonding material) resists the relative translation and rotation of neighboring PbS particles. In DEM simulations bonding material is usually taken into account implicitly using the concept of so-called bonds. Neighboring particles are connected by the bonds that resist to stretching/compression, shear, bending, and torsion. The bonds cause forces and torques acting on the particles along with contact forces. Mass of the bonding material is usually neglected. The assumption does not influence static properties of the granular material. The influence on the dynamic properties is not so straightforward and should be considered separately. However let us note that in many practical applications the mass of bonding material is much smaller than the mass of the particles (see, for example, figures below). Therefore the mass of bonding material can be neglected.

Discrete Rod: SEM image of 1D assembly of particles embedded in polymer matrix (M. Wang, et.al., Materials Today, Vol. 16, No. 4, 2013)
Discrete Shell: Colloidsome composed of polysterene spheres (A.D. Dismore, et.al. Science, 2002)
Discrete Solid: aerogel (source)

In the paper V.A. Kuzkin and I.E. Asonov "Vector-based model of elastic bonds for simulation of granullar solids"// Phys. Rev. E, 86, 051301, 2012 vector-based model(the V-model) of elastic bonds in solids is developed. Equations describing interactions between two rigid bodies in the general case are summarized. The general expression for the potential energy of the bond is represented via vectors rigidly connected with bonded particles. The vectors are used for description of different types of bond's deformation. The expression for potential energy corresponding to tension/compression, shear, bending, and torsion of the bond is proposed. Forces and torques acting between particles are derived from the potential energy. Two approaches for calibration of V-model parameters for bonds with different length/thickness ratios are presented. Simple analytical formulas connecting geometrical and elastic characteristics of the bond with parameters of the V-model are derived. Main aspects of numerical implementation of the model are discussed.

V-model

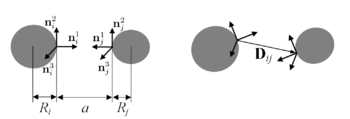
The V-model is based on the combination of approaches proposed in works of P.A. Zhilin, E.A. Ivanova, A.M. Krivtsov, N.F. Morozov [1], [2] and works of M.P. Allen [3], S.L Price. The main idea is to represent potential energy of the bond as a function of vectors connected with bonded particles.

Vectors connected with the particles
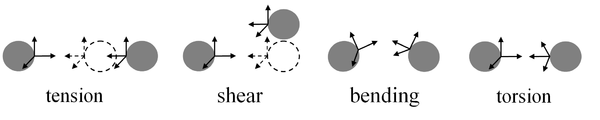
Different deformations of the bond.

Different kinds of deformation of the bond and corresponding change in vectors, connected with the particles is shown below. Dashed lines show initial state of the particles.

Detailed description of the model and procedures for parameters calibration are given in the paper. Here let us show some results obtained using the V-model.

Rod under the action of following shear force, acting on the rod's end
Plate under the action of following compressive forces, acting along the edge of the plate
Torsion of 3D rod-like body

Advantages of V-model

Let us summarize advantages of V-model:

  • longitudinal, shear, bending, and torsional stiffnesses of the bond are independent
  • applicable in the case of large turns of the particles
  • conservation of energy (bonds are perfectly elastic)
  • any non close packed structure, rods and shells can be simulated(see figures above)
  • forces and torques are calculated as a functions of particles' positions and orientations (more accurate integration of motion equations than in the case of incremental algorithm used for BPM)
  • description of bonds of any length/thickness ratio. It is shown that in the case of small deformations the behavior of the bond can fit the behavior of Bernulli-Euler rod or Timosheko rod or short cylinder connecting particles (depending on length/thickness ratio)
  • simple analytical expressions connecting parameters of V-model with geometrical and mechanical characteristics of the bond
  • bonds can connect points inside the particles or lying on particles surfaces (not only particle centers)
  • fracture criterion for the bond can be used if required

Debugging

The simplest way of debugging is a solution of the following four test problems for the system of 2 bonded particles. In all four cases forces and torques acting on the particles can be calculated both analytically and numerically. Obviously, the results should coincide.

  • Pure stretching. Porition of one particle is fixed. Another particle is moving along the line connecting particles with constant velocity. The force acting on the particles is calculated.
  • Pure shear. Orientations of the particles are fixed. Position of one particle if fixed. Another particle is moving (with constant velocity) along the line, orthogonal to initial direction of the bond. The force and torques acting on the particles are calculated.
  • Pure bending. Positions of both particles are fixed and the particles are rotated along the same axis, orthogonal to the bond, but in opposite directions. The torque acting on the particles is calculated.
  • Pure torsion. Positions of both particles are fixed. Orientation of one particle is fixed. Another particle is rotating around the bond. The torque acting on the particles is calculated.


DEM packages using V model

  • LIGGGHTS, details of implementation and some examples are given here.

History and acknowledgements

The idea underlining V-model was first formulated by Vitaly Kuzkin during communication with Michael Wolff in Technical University of Hamburg (March, 2011). The first formulation was very simple and coarse, but it works! The results of some test simulations were presented by Vitaly Kuzkin on APM 2011 conference (July, 2011). At the present moment V-model is much more flexible and physically meaningful than its first version. Now it is developed jointly by Vitaly Kuzkin and Igor Asonov. The V-model is implemented in DEM package LIGGGHTS by Patrick Fodor.

The authors are deeply grateful to Michael Wolff, Prof. Anton Krivtsov, Prof. Stephan Heinrich, Dr. Sergiy Antonyuk and Prof. William Hoover.

References

  1. ↑ E.A. Ivanova, A. M. Krivtsov, N. F. Morozov, A. D. Firsova. Decsription of crystal particle packing considering moment interactions // Mechanics of Solids. 2003. Vol. 38. No 4, pp. 101-117.
  2. ↑ E. A. Ivanova, A. M. Krivtsov, N. F. Morozov, Derivation of macroscopic relations of the elasticity of complex crystal lattices taking into account the moment interactions at the microlevel // J. App. Math. and Mech.,Vol. 71, Is. 4, 2007, pp. 543-561.
  3. ↑ M.P. Allen, D.J. Tildesley, Computer simulation of liquids, Clarendon Press, Oxford, 1987, p. 385.

Ошибка цитирования Тег <ref> с именем «BPM», определённый в <references>, не используется в предшествующем тексте.
Ошибка цитирования Тег <ref> с именем «Wang», определённый в <references>, не используется в предшествующем тексте.

Links

Источник — «http://tm.spbstu.ru/?title=V-model&oldid=21922»