Manipulator model — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
(→‎Hand rotation)
(→‎Hand rotation)
Строка 31: Строка 31:
 
<math>Q = (w,x,y,z) = w + xi + yj + zk</math> , where i,j,k satisfies <br>
 
<math>Q = (w,x,y,z) = w + xi + yj + zk</math> , where i,j,k satisfies <br>
 
<math>i^2 = j^2 = k^2 = ijk = -1</math><br>
 
<math>i^2 = j^2 = k^2 = ijk = -1</math><br>
 +
====Useful formulas====
 +
We are going to use quaternion written as<br>
 +
<math>Q = [w,v]</math> - where <math>w</math> - scalar and <math>v</math> - vector <br>
 +
In these terms we have rotation quaternion<br>
 +
<math>Q = \left[ \cos \left( \frac{\alpha}{2} \right), \sin \left( \frac{\alpha}{2} \right)v  \right]</math><br>
 +
This is the quaternion that rotates round vector <math>v</math> on angle <math>\alpha</math><br>
 +
<math>Q* = [w, -v]</math> - conjugated quaternion<br>
 +
<math>norm(Q) = \sqrt{w^2 + x^2 + y^2 +z^2}</math> - norm of quaternion<br>
 +
<math>Q^{-1} = \frac{Q*}{norm(Q)}</math> - reverse quaternion<br>
 +
<math>QQ' = [ ww' - v \cdot v', v \times v' + wv' + w' v]</math> - quaternion multiplication <br>
 +
====Vector rotation====
 +
In order to rotate the vector <math>r</math> we need to go through the following steps:<br>
 +
'''1) Cast vector to quaternion''' It's easy to make quaternion of vector. Just add zero to the scalar part and your vector to the vector part of quaternion<br>
 +
<math>R = [0,r]</math><br>
 +
'''2) Multiply''' <br>
 +
<math>R' = Q R Q^{-1}</math><br>
 +
'''3)'''

Версия 18:48, 9 ноября 2012

TM 1.jpg

Description

This is the page of a project related to project "Fencing".

Developers

Dzenushko Dainis

Global Task

The main aim of this project is development of a program which will be useful for recording and calculation of manipulator's movement.

Current task

Current task is development of fencer's hand model. That means to create mathematical model, that finds the position of a hand and comes to this position from any previous position with visualization on C# language, using parameters (changes of angles in joints and coordinates of a shoulder)

Some information about programm

Degrees of freedom

This model has 9 degrees of freedom:
2 — translation movement of a shoulder (front/back; up/down)
3 — shoulder joint as a ball joint
1 — elbow joint 
1 — rotation of wrist round it’s axis
2 — wrist (2 perpendicular cylindrical joints)

Hand rotation

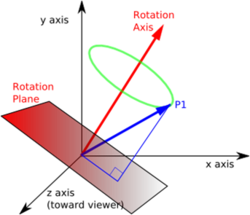
Vector rotation.png

In order to rotate any 3D object we should rotate related vector.
But how to rotate vector?
This programm uses quaternions for vector rotation.

Quaternions

Usually quaternions are defined as a number system that extends the complex numbers to 4D space. In a simplier way we can define quaternions as 4 numbers with specific operations and properties.
[math]Q = (w,x,y,z) = w + xi + yj + zk[/math] , where i,j,k satisfies
[math]i^2 = j^2 = k^2 = ijk = -1[/math]

Useful formulas

We are going to use quaternion written as
[math]Q = [w,v][/math] - where [math]w[/math] - scalar and [math]v[/math] - vector
In these terms we have rotation quaternion
[math]Q = \left[ \cos \left( \frac{\alpha}{2} \right), \sin \left( \frac{\alpha}{2} \right)v \right][/math]
This is the quaternion that rotates round vector [math]v[/math] on angle [math]\alpha[/math]
[math]Q* = [w, -v][/math] - conjugated quaternion
[math]norm(Q) = \sqrt{w^2 + x^2 + y^2 +z^2}[/math] - norm of quaternion
[math]Q^{-1} = \frac{Q*}{norm(Q)}[/math] - reverse quaternion
[math]QQ' = [ ww' - v \cdot v', v \times v' + wv' + w' v][/math] - quaternion multiplication

Vector rotation

In order to rotate the vector [math]r[/math] we need to go through the following steps:
1) Cast vector to quaternion It's easy to make quaternion of vector. Just add zero to the scalar part and your vector to the vector part of quaternion
[math]R = [0,r][/math]
2) Multiply
[math]R' = Q R Q^{-1}[/math]
3)

Источник — «http://tm.spbstu.ru/?title=Manipulator_model&oldid=14589»