Моделирование распространения тепла в треугольной кристаллической решетке — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
(→‎Описание алгоритма)
(→‎Описание алгоритма)
 
(не показано 11 промежуточных версий этого же участника)
Строка 1: Строка 1:
  
 
== Постановка Задачи ==
 
== Постановка Задачи ==
−
Исследовать процесс распространения тепла в бесконечной треугольной скалярной кристаллической решетке. Сформулировать и поставить численный эксперимент, который будет наиболее точно соответствовать теоретической задаче.  
+
Численно смоделировать процесс распространения тепла в бесконечной треугольной скалярной кристаллической решетке на примере фундаментального решения и синусоидального распределения. Численно смоделировать колебания кинетической температуры для однородно-нагретой решетки. Сравнить решения, полученные из численных экспериментов с аналитическим решением.
 
=== Кристаллическая решетка ===
 
=== Кристаллическая решетка ===
−
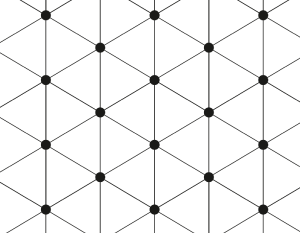
Рассматривается плоская кристаллическая скалярная решетка. Атомы этой решетки расположены в вершинах равных правильных треугольников и имеют одинаковую массу m. Связи между атомами моделируются линейными пружинками с жесткостью k. Каждый атом имеет одну степень свободы - он может двигаться вдоль прямой, перпендикулярной плоскости решетки. Схематически решетка представлена на рисунке 1.
+
Рассматривается плоская кристаллическая скалярная решетка. Атомы этой решетки расположены в вершинах равных правильных треугольников и имеют одинаковую массу m. Каждый атом имеет одну степень свободы - он может двигаться вдоль прямой, перпендикулярной плоскости решетки. Схематически решетка представлена на рисунке 1.
−
[[File:Lattice 1|thumb|left|Внешний вид кристаллической решетки]]
+
[[File:Lattice — копия.bmp|thumb|center|Треугольная кристаллическая решетка]]
−
Процесс распространения тепловой энергии в кристалле проходит на молекулярном уровне, как следствие материалы с правильной регулярной структурой могут обладать особыми свойствами теплопроводности, которые могут зависеть от направления. Для исследования свойств теплопроводности в каком-то одном из направлений необходимо смоделировать бесконечную плоскую решетку, задать температуру вдоль выделенного направления (при этом во всех точках, лежащих на одной прямой, перпендикулярной выделенному направлению температура будет одинаковой) и наблюдать за скоростью, с которой тепловая энергия будет распределяться в кристалле. Чем быстрее температура выравнивается, тем больше теплопроводность кристалла в данном направлении.
+
Процесс распространения тепловой энергии в кристалле проходит на молекулярном уровне, как следствие материалы с правильной регулярной структурой могут обладать особыми свойствами теплопроводности, которые могут зависеть от направления. Для исследования свойств теплопроводности в каком-то одном из направлений необходимо смоделировать бесконечную плоскую решетку, задать температуру вдоль выделенного направления (при этом во всех точках, лежащих на одной прямой, перпендикулярной выделенному направлению температура будет одинаковой) и наблюдать за скоростью, с которой тепловая энергия будет распределяться в кристалле. От скорости выравнивания температуры зависят свойства теплопроводности вещества в данном направлении.
  
 
=== Периодичные начальные условия ===
 
=== Периодичные начальные условия ===
 
К сожалению, расчет бесконечной решетки (и как следствие бесконечного числа частиц) потребовал бы бесконечных вычислительных мощностей или бесконечного времени на расчет. Если ограничиться достаточно большой решеткой, но конечных размеров, это приведет к ухудшению точности в связи с влиянием эффектов на границе и потребует значительных ресурсов при вычислениях. Из этой ситуации позволяет выйти периодичность кристаллической решетки. Если задать начальное одномерное распределение температуры, которое можно задать также периодичным. Таким образом мы получаем, что всю бесконечную плоскость можно разбить на конечные участки, на каждом из которых будут одинаковые начальные условия и одинаковая геометрия решетки. Это позволяет заменить задачу про бесконечную плоскость на задачу о конечном участке с периодичными граничными условиями. В качестве периодичной функции температуры вдоль выделенного направления использован синус. Распределение температуры в пространстве задавалось законом:
 
К сожалению, расчет бесконечной решетки (и как следствие бесконечного числа частиц) потребовал бы бесконечных вычислительных мощностей или бесконечного времени на расчет. Если ограничиться достаточно большой решеткой, но конечных размеров, это приведет к ухудшению точности в связи с влиянием эффектов на границе и потребует значительных ресурсов при вычислениях. Из этой ситуации позволяет выйти периодичность кристаллической решетки. Если задать начальное одномерное распределение температуры, которое можно задать также периодичным. Таким образом мы получаем, что всю бесконечную плоскость можно разбить на конечные участки, на каждом из которых будут одинаковые начальные условия и одинаковая геометрия решетки. Это позволяет заменить задачу про бесконечную плоскость на задачу о конечном участке с периодичными граничными условиями. В качестве периодичной функции температуры вдоль выделенного направления использован синус. Распределение температуры в пространстве задавалось законом:
 
::<math>
 
::<math>
−
     T = T_0 sin (\omega x)
+
     T = T_0 (\sin{\omega x}+1.05)
 
</math>
 
</math>
 
в первом случае и  
 
в первом случае и  
 
::<math>
 
::<math>
−
     T = T_0 sin (\omega y),
+
     T = T_0 (\sin{\omega y}+1.05),
 
</math>
 
</math>
−
где x,y - декартовы координаты в плоскости решетки
+
где x,y - декартовы координаты в плоскости решетки, слагаемое 1.05 вводится для строгой положительности температуры во всех точках
  
 
=== Периодические граничные условия ===
 
=== Периодические граничные условия ===
 
Бесконечную плоскость треугольной кристаллической решетки можно разбивать на фигуры различных форм и размеров. Но наиболее простыми и оптимальными вариантами являются шестиугольники и прямоугольники (конечно, две из сторон такого прямоугольника не будут прямыми из-за геометрии решетки). Поскольку начальные условия задачи имеют одно выделенное направление, то единственным подходящим вариантов ячейки периодичности решетки является прямоугольник.
 
Бесконечную плоскость треугольной кристаллической решетки можно разбивать на фигуры различных форм и размеров. Но наиболее простыми и оптимальными вариантами являются шестиугольники и прямоугольники (конечно, две из сторон такого прямоугольника не будут прямыми из-за геометрии решетки). Поскольку начальные условия задачи имеют одно выделенное направление, то единственным подходящим вариантов ячейки периодичности решетки является прямоугольник.
−
[[File:lattice.png|200px|thumb|left|Внешний вид ячейки периодичности]]
+
[[File:lattice.png|200px|thumb|center|Внешний вид ячейки периодичности]]
 
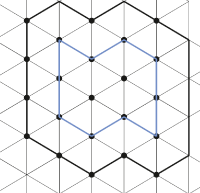
Синим контуром обведены частицы, которые являются уникальными (не повторяющимися), а черным контуром – частицы, данные о которых хранятся и обрабатываются в программе. Размеры решетки, используемой для расчетов много больше представленных на рисунке и составляют порядка сотни частиц.
 
Синим контуром обведены частицы, которые являются уникальными (не повторяющимися), а черным контуром – частицы, данные о которых хранятся и обрабатываются в программе. Размеры решетки, используемой для расчетов много больше представленных на рисунке и составляют порядка сотни частиц.
  
−
=== Описание алгоритма ===
+
== Описание алгоритма ==
 
В данной программе решается задача для двух направлений – вдоль одного из направлений связей и перпендикулярно ему. Основные этапы расчета содержат:
 
В данной программе решается задача для двух направлений – вдоль одного из направлений связей и перпендикулярно ему. Основные этапы расчета содержат:
−
# Создание начальной конфигурации решетки, массива температур. Для каждого ряда (или столбца) высчитывается его температура по формуле
+
Создание начальной конфигурации решетки, массива температур. Для каждого ряда (или столбца) высчитывается его температура по формуле
 
::<math>
 
::<math>
−
    T = T_0 sin (\omega x).
+
T_0 = T_b+\Delta T \sin{ \frac{2 \pi x \cdot \textbf{e_t}}{L}}
 
</math>
 
</math>
−
Далее всем точкам этого ряда (столбца) задаются случайные скорости, такие, что значение квадрата их модуля не превышает температуры данного ряда (столбца)
+
Далее всем точкам этого ряда (столбца) задаются случайные скорости, такие, что значение квадрата их модуля не превышает температуры данного ряда (столбца)
 
::<math>
 
::<math>
−
     V_0 = random(-K \sqrt{T(x); K \sqrt{T(x)}}
+
     V_0 = random(-\sqrt{\frac{3k_b T(x)}{m}}; \sqrt{\frac{3k_b T(x)}{m}}).
−
</math>. Положение всех точек в начальный момент времени соответствует равновесному положению. Такие начальные условия не являются реалистичными, поскольку вся энергия системы является кинетической. Но, как показывает эксперимент, через некоторое время колебания потенциальной и кинетической энергии затухают и их значения во все последующие моменты времени практически равны (что и наблюдается в реальных системах). Поэтому такой подход допустим с оговоркой, что при временах меньше 2T0 (характерное время колебания системы) результаты нельзя использовать напрямую для прогнозирования поведения реальных систем.
+
</math>. Положение всех точек в начальный момент времени соответствует равновесному положению. Как показывает эксперимент, через некоторое время колебания потенциальной и кинетической энергии затухают и их значения во все последующие моменты времени практически равны (что и наблюдается в реальных системах). Поэтому такой подход допустим с оговоркой, что при временах меньше 2T0 (характерное время колебания системы) результаты нельзя использовать напрямую для прогнозирования поведения реальных систем.
−
# Расчет одного шага по времени. На этом этапе проводилось интегрирование системы уравнений движения  методом Эйлера, который имеет ошибку порядка O(h). Для удобства решения задачи, помимо «уникальных» частиц в массиве содержатся также их копии, которые образуют внешний слой рассматриваемого участка. Интегрирование производилось только для «уникальных» частиц. Остальные частицы (внешний слой) получались копированием «уникальных». Для этого использовались формулы
+
 
 +
Расчет одного шага по времени. На этом этапе проводилось интегрирование системы уравнений движения  методом Эйлера, который имеет ошибку порядка O(h). Для удобства решения задачи, помимо «уникальных» частиц в массиве содержатся также их копии, которые образуют внешний слой рассматриваемого участка. Интегрирование производилось только для «уникальных» частиц. Остальные частицы (внешний слой) получались копированием «уникальных». Для этого использовались формулы
 
::<math>
 
::<math>
 
\ddot{u} = \frac{c}{m}(u_{i+1,j+1}+u_{i+1,j-1}+u_{i+1,j}+u_{i,j+1}+ u_{i,j-1}+u_{i-1,j} - 6 u_{i,j});\text{    }    j =2n  
 
\ddot{u} = \frac{c}{m}(u_{i+1,j+1}+u_{i+1,j-1}+u_{i+1,j}+u_{i,j+1}+ u_{i,j-1}+u_{i-1,j} - 6 u_{i,j});\text{    }    j =2n  
Строка 42: Строка 43:
 
</math>
 
</math>
 
# Осреднение по множеству реализаций. Поскольку температура – величина статистическая, то неправомерно считать ее как квадрат скорости частицы на некий коэффициент. Поэтому для достижения более высокой точности в программе создается несколько наборов начальных скоростей для частиц, каждый из которых отвечает начальному распределению температуры. При подсчете температуры используется осреднение значений по всем реализациям.
 
# Осреднение по множеству реализаций. Поскольку температура – величина статистическая, то неправомерно считать ее как квадрат скорости частицы на некий коэффициент. Поэтому для достижения более высокой точности в программе создается несколько наборов начальных скоростей для частиц, каждый из которых отвечает начальному распределению температуры. При подсчете температуры используется осреднение значений по всем реализациям.
−
# Вычисление амплитуды. Этот этап необходим непосредственно для определения теплопроводности в данном направлении. Амплитуда высчитывается как скалярное произведение температуры в данный момент времени и синуса той же частоты, что и в начальных условиях (интегрирование по периоду).
+
# Вычисление амплитуды. Амплитуда высчитывается как скалярное произведение температуры в данный момент времени и синуса той же частоты, что и в начальных условиях (интегрирование по периоду).
 
::<math>
 
::<math>
−
     A = \int_0^l T(x) sin(\omega x) dx
+
     A = \int_0^l T(x) \sin{\omega x} dx
 
</math>
 
</math>
  
−
=== Результаты ===
+
== Результаты ==
 +
 
 +
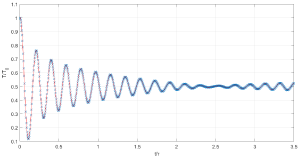
Численное решение (крестики) и аналитическое решение (красная линия) для случая однородно нагретой решетки. График зависимости кинетической температуры от времени
 +
 
 +
[[File:Fast proc.png|thumb|center|Зависимость кинетической температуры однородно нагретой решетки от времени.]]
 +
 
 
В результате численного эксперимента были получены следующий графики:
 
В результате численного эксперимента были получены следующий графики:
−
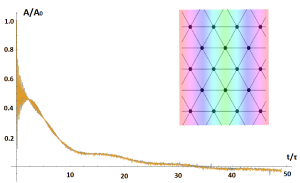
# График зависимости амплитуды от времени при T_max = 10 T0, dt = 0.001 T0, ось вдоль связей, 200 точек.
 
  
−
[[File:Oy_10T0.jpg|thumb|амплитуда синуса по y]]
+
График зависимости амплитуды от времени при T_max = 50 T0, dt = 0.001 T0, ось распространения тепла - вдоль межатомных связей.
 +
 
 +
[[File:X 1000 points 50T0 p.png|thumb|center|Амплитуда температурного синуса при модуляции вдоль направления межатомных связей]]
 +
 
 +
График зависимости амплитуды от времени при T_max = 50 T0, dt = 0.001 T0, ось распространения тепла - перпендикулярно направлению межатомных связей.
 +
 
 +
[[File:Y 1000 points 50T0 p.png|thumb|center|амплитуда температурного синуса при модуляции перпендикулярно направлению межатомных связей]]
 +
 
 +
Было проведено моделирование распространения тепла для случая фундаментального решения. Результат представлен на рисунке ниже:
 +
 
 +
[[File:R10nrand1000l10001000.png|thumb|center|Построение фундаментального решения с помощью численного эксперимента]]
 +
 
 +
Визуализация аналитического решения имеет для фундаментального решения представлена на следующем рисунке:
 +
 
 +
[[File:FS3copcop.jpg|thumb|center|Фундаментальное решение, полученное аналитически]]
 +
 
 +
==Выводы:==
 +
# Фронт имеет форму окружности для фундаментального решения.
 +
# Теплопроводящие свойства для треугольной решетки анизотропны, несмотря на изотропию упругих свойств.
 +
# Аналитическое решение предсказывает результаты численного эксперимента с высокой точностью
 +
# При перераспределении температуры вдоль направления межатомных связей устанавливается температурное поле, в котором «горячие» и «холодные» области меняются местами.
 +
===Материалы по теме===
 +
[[File:Davydova Poster.docx|thumb|Постер в формате docx]] - Постер в формате docx
 +
 
 +
[[File:DIPLOM.pdf|thumb|Полный текст дипломной работы]] - Полный текст дипломной работы
 +
 
 +
[[File:Давыдова Слайд.pptx|thumb|Слайд о работе в формате pptx]] - Слайд о работе в формате pptx
  
−
# График зависимости амплитуды от времени при T_max = 10 T0, dt = 0.001 T0, ось перпендикулярна одному из направлений связей, 200 точек.
+
[[File:Presentation1.pdf|thumb|Презентация с защиты]] - Презентация с защиты
−
[[File:Ox_10T0.jpg|thumb|left|График зависимости амплитуды синуса температур от времени (вдоль оси x)]]
 
−
В результате анализа графиков было получено, что тепло распространяется в двух исследуемых направлениях одинаково, при том, что геометрия решетки не является симметричной относительно поворота на 90 градусов. Возможно, из этого эксперимента следует, что теплопроводность треугольной решетки вообще во всех направлениях одинакова.(но это не точно)
 
  
−
=== Ссылки ===
+
== Ссылки ==
 
#[[Курсовые_работы_по_ВМДС:_2018-2019]]
 
#[[Курсовые_работы_по_ВМДС:_2018-2019]]
 
#Автор работы - [[Давыдова Алена]]
 
#Автор работы - [[Давыдова Алена]]
 
#Руководитель - [[Виталий Андреевич Кузькин]]
 
#Руководитель - [[Виталий Андреевич Кузькин]]
 +
# [[Проект "Термокристалл"]]
  
−
=== Список использованной литературы ===
+
== Список использованной литературы ==
 +
# Кривцов А.М. Кузькин В.А. Механика дискретных сред. Переходные тепловые процессы в гармонических кристалла: учебное пособие [Книга]. - Спб : Политехн. ун-та, 2017.
 +
# Lepri S. Thermal transport in low dimensions: from statistical physics to nanoscale heat transfer [Book]. - [s.l.] : Springer, 2016. - Vol. 921.
 +
# Абдуллаев Н. А. Особенности упругих свойств слоистых кристаллов [Статья] // Физика твердого тела.. - 2006 г.. - 4 – С. 623-629 : Т. 48.
 +
# Феофилов П. П. Каплянский А. А. Скрытая оптическая анизотропия кубических кристаллов, содержащих локальные центры, и методы ее исследования [Статья] // Успехи физических наук. - 1962 г.. - 2 : Т. 76.
 +
# D.G. Cahill W.K. Ford, K.E. Goodson, G.D. Mahan, A. Majumdar, H.J. Maris, R. Nanoscale thermal transport [Article] // Journal of Applied Physics 93, 793. - 27 December 2003.
 +
# T.Y. Chen C.L. Chien, M. Manno, L. Wang, C. Leighton Ballistic heat transport in nanocontacts [Статья] // Physical Review B.. - 2010 г.. - 2 : Т. 81.
 +
# Krivtsov Vitaly A. Kuzkin Anton M. Fast and slow thermal processes in harmonic scalar [Статья] // Journal of Physics: Condensed Matter. - [б.м.] : IOP Publishing Ltd, 2017 г.. - 50 : Т. 29.
 +
# Kuzkin Vitaly A. Unsteady ballistic heat transport in harmonic crystals [Статья]. - 2019 г..
 +
# S. Liu X.F. Xu, R.G. Xie, G. Zhang, B.W. Li Anomalous heat conduction and anomalous diffusion in low dimensional nanoscale systems [Статья] // The European Physical Journal B,. - 2012 г.. - 10 : Т. 85.
 +
# Tsaplin V. A. Kuzkin V. A. Temperature oscillations in harmonic triangular lattice [Статья] // Letters on Materials. - 2018 г.. - 1 : Т. 8.

Текущая версия на 14:10, 8 июля 2019

Постановка Задачи[править]

Численно смоделировать процесс распространения тепла в бесконечной треугольной скалярной кристаллической решетке на примере фундаментального решения и синусоидального распределения. Численно смоделировать колебания кинетической температуры для однородно-нагретой решетки. Сравнить решения, полученные из численных экспериментов с аналитическим решением.

Кристаллическая решетка[править]

Рассматривается плоская кристаллическая скалярная решетка. Атомы этой решетки расположены в вершинах равных правильных треугольников и имеют одинаковую массу m. Каждый атом имеет одну степень свободы - он может двигаться вдоль прямой, перпендикулярной плоскости решетки. Схематически решетка представлена на рисунке 1.

Треугольная кристаллическая решетка

Процесс распространения тепловой энергии в кристалле проходит на молекулярном уровне, как следствие материалы с правильной регулярной структурой могут обладать особыми свойствами теплопроводности, которые могут зависеть от направления. Для исследования свойств теплопроводности в каком-то одном из направлений необходимо смоделировать бесконечную плоскую решетку, задать температуру вдоль выделенного направления (при этом во всех точках, лежащих на одной прямой, перпендикулярной выделенному направлению температура будет одинаковой) и наблюдать за скоростью, с которой тепловая энергия будет распределяться в кристалле. От скорости выравнивания температуры зависят свойства теплопроводности вещества в данном направлении.

Периодичные начальные условия[править]

К сожалению, расчет бесконечной решетки (и как следствие бесконечного числа частиц) потребовал бы бесконечных вычислительных мощностей или бесконечного времени на расчет. Если ограничиться достаточно большой решеткой, но конечных размеров, это приведет к ухудшению точности в связи с влиянием эффектов на границе и потребует значительных ресурсов при вычислениях. Из этой ситуации позволяет выйти периодичность кристаллической решетки. Если задать начальное одномерное распределение температуры, которое можно задать также периодичным. Таким образом мы получаем, что всю бесконечную плоскость можно разбить на конечные участки, на каждом из которых будут одинаковые начальные условия и одинаковая геометрия решетки. Это позволяет заменить задачу про бесконечную плоскость на задачу о конечном участке с периодичными граничными условиями. В качестве периодичной функции температуры вдоль выделенного направления использован синус. Распределение температуры в пространстве задавалось законом:

[math] T = T_0 (\sin{\omega x}+1.05) [/math]

в первом случае и

[math] T = T_0 (\sin{\omega y}+1.05), [/math]

где x,y - декартовы координаты в плоскости решетки, слагаемое 1.05 вводится для строгой положительности температуры во всех точках

Периодические граничные условия[править]

Бесконечную плоскость треугольной кристаллической решетки можно разбивать на фигуры различных форм и размеров. Но наиболее простыми и оптимальными вариантами являются шестиугольники и прямоугольники (конечно, две из сторон такого прямоугольника не будут прямыми из-за геометрии решетки). Поскольку начальные условия задачи имеют одно выделенное направление, то единственным подходящим вариантов ячейки периодичности решетки является прямоугольник.

Внешний вид ячейки периодичности

Синим контуром обведены частицы, которые являются уникальными (не повторяющимися), а черным контуром – частицы, данные о которых хранятся и обрабатываются в программе. Размеры решетки, используемой для расчетов много больше представленных на рисунке и составляют порядка сотни частиц.

Описание алгоритма[править]

В данной программе решается задача для двух направлений – вдоль одного из направлений связей и перпендикулярно ему. Основные этапы расчета содержат: Создание начальной конфигурации решетки, массива температур. Для каждого ряда (или столбца) высчитывается его температура по формуле

[math] T_0 = T_b+\Delta T \sin{ \frac{2 \pi x \cdot \textbf{e_t}}{L}} [/math]

Далее всем точкам этого ряда (столбца) задаются случайные скорости, такие, что значение квадрата их модуля не превышает температуры данного ряда (столбца)

[math] V_0 = random(-\sqrt{\frac{3k_b T(x)}{m}}; \sqrt{\frac{3k_b T(x)}{m}}). [/math]. Положение всех точек в начальный момент времени соответствует равновесному положению. Как показывает эксперимент, через некоторое время колебания потенциальной и кинетической энергии затухают и их значения во все последующие моменты времени практически равны (что и наблюдается в реальных системах). Поэтому такой подход допустим с оговоркой, что при временах меньше 2T0 (характерное время колебания системы) результаты нельзя использовать напрямую для прогнозирования поведения реальных систем.

Расчет одного шага по времени. На этом этапе проводилось интегрирование системы уравнений движения методом Эйлера, который имеет ошибку порядка O(h). Для удобства решения задачи, помимо «уникальных» частиц в массиве содержатся также их копии, которые образуют внешний слой рассматриваемого участка. Интегрирование производилось только для «уникальных» частиц. Остальные частицы (внешний слой) получались копированием «уникальных». Для этого использовались формулы

[math] \ddot{u} = \frac{c}{m}(u_{i+1,j+1}+u_{i+1,j-1}+u_{i+1,j}+u_{i,j+1}+ u_{i,j-1}+u_{i-1,j} - 6 u_{i,j});\text{ } j =2n [/math]
[math] \ddot{u} = \frac{c}{m}(u_{i-1,j+1}+u_{i-1,j-1}+u_{i-1,j}+u_{i,j+1}+ u_{i,j-1}+u_{i+1,j} - 6 u_{i,j});\text{ } j =2n+1 [/math]
  1. Осреднение по множеству реализаций. Поскольку температура – величина статистическая, то неправомерно считать ее как квадрат скорости частицы на некий коэффициент. Поэтому для достижения более высокой точности в программе создается несколько наборов начальных скоростей для частиц, каждый из которых отвечает начальному распределению температуры. При подсчете температуры используется осреднение значений по всем реализациям.
  2. Вычисление амплитуды. Амплитуда высчитывается как скалярное произведение температуры в данный момент времени и синуса той же частоты, что и в начальных условиях (интегрирование по периоду).
[math] A = \int_0^l T(x) \sin{\omega x} dx [/math]

Результаты[править]

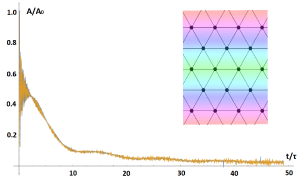
Численное решение (крестики) и аналитическое решение (красная линия) для случая однородно нагретой решетки. График зависимости кинетической температуры от времени

Зависимость кинетической температуры однородно нагретой решетки от времени.

В результате численного эксперимента были получены следующий графики:

График зависимости амплитуды от времени при T_max = 50 T0, dt = 0.001 T0, ось распространения тепла - вдоль межатомных связей.

Амплитуда температурного синуса при модуляции вдоль направления межатомных связей

График зависимости амплитуды от времени при T_max = 50 T0, dt = 0.001 T0, ось распространения тепла - перпендикулярно направлению межатомных связей.

амплитуда температурного синуса при модуляции перпендикулярно направлению межатомных связей

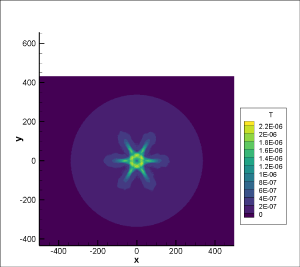
Было проведено моделирование распространения тепла для случая фундаментального решения. Результат представлен на рисунке ниже:

Построение фундаментального решения с помощью численного эксперимента

Визуализация аналитического решения имеет для фундаментального решения представлена на следующем рисунке:

Фундаментальное решение, полученное аналитически

Выводы:[править]

  1. Фронт имеет форму окружности для фундаментального решения.
  2. Теплопроводящие свойства для треугольной решетки анизотропны, несмотря на изотропию упругих свойств.
  3. Аналитическое решение предсказывает результаты численного эксперимента с высокой точностью
  4. При перераспределении температуры вдоль направления межатомных связей устанавливается температурное поле, в котором «горячие» и «холодные» области меняются местами.

Материалы по теме[править]

Файл:Davydova Poster.docx - Постер в формате docx

Файл:DIPLOM.pdf - Полный текст дипломной работы

Файл:Давыдова Слайд.pptx - Слайд о работе в формате pptx

Файл:Presentation1.pdf - Презентация с защиты

Ссылки[править]

  1. Курсовые_работы_по_ВМДС:_2018-2019
  2. Автор работы - Давыдова Алена
  3. Руководитель - Виталий Андреевич Кузькин
  4. Проект "Термокристалл"

Список использованной литературы[править]

  1. Кривцов А.М. Кузькин В.А. Механика дискретных сред. Переходные тепловые процессы в гармонических кристалла: учебное пособие [Книга]. - Спб : Политехн. ун-та, 2017.
  2. Lepri S. Thermal transport in low dimensions: from statistical physics to nanoscale heat transfer [Book]. - [s.l.] : Springer, 2016. - Vol. 921.
  3. Абдуллаев Н. А. Особенности упругих свойств слоистых кристаллов [Статья] // Физика твердого тела.. - 2006 г.. - 4 – С. 623-629 : Т. 48.
  4. Феофилов П. П. Каплянский А. А. Скрытая оптическая анизотропия кубических кристаллов, содержащих локальные центры, и методы ее исследования [Статья] // Успехи физических наук. - 1962 г.. - 2 : Т. 76.
  5. D.G. Cahill W.K. Ford, K.E. Goodson, G.D. Mahan, A. Majumdar, H.J. Maris, R. Nanoscale thermal transport [Article] // Journal of Applied Physics 93, 793. - 27 December 2003.
  6. T.Y. Chen C.L. Chien, M. Manno, L. Wang, C. Leighton Ballistic heat transport in nanocontacts [Статья] // Physical Review B.. - 2010 г.. - 2 : Т. 81.
  7. Krivtsov Vitaly A. Kuzkin Anton M. Fast and slow thermal processes in harmonic scalar [Статья] // Journal of Physics: Condensed Matter. - [б.м.] : IOP Publishing Ltd, 2017 г.. - 50 : Т. 29.
  8. Kuzkin Vitaly A. Unsteady ballistic heat transport in harmonic crystals [Статья]. - 2019 г..
  9. S. Liu X.F. Xu, R.G. Xie, G. Zhang, B.W. Li Anomalous heat conduction and anomalous diffusion in low dimensional nanoscale systems [Статья] // The European Physical Journal B,. - 2012 г.. - 10 : Т. 85.
  10. Tsaplin V. A. Kuzkin V. A. Temperature oscillations in harmonic triangular lattice [Статья] // Letters on Materials. - 2018 г.. - 1 : Т. 8.
Источник — «http://tm.spbstu.ru/?title=Моделирование_распространения_тепла_в_треугольной_кристаллической_решетке&oldid=54093»