Решение задач механики сплошной среды для слоистых структур — различия между версиями
Mksf (обсуждение | вклад) |
Mksf (обсуждение | вклад) |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 82: | Строка 82: | ||
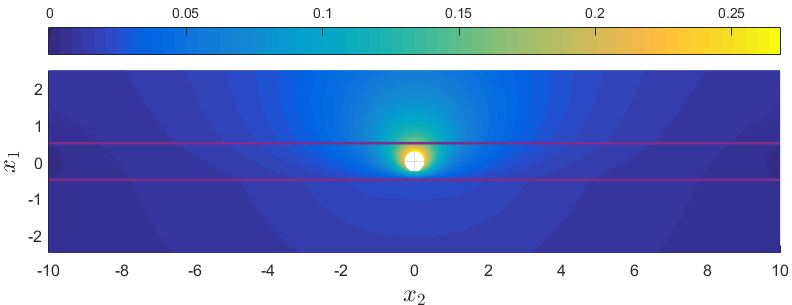
==Пример: круговое отверстие в слоистой структуре для оператора Лапласа== | ==Пример: круговое отверстие в слоистой структуре для оператора Лапласа== | ||
Рассмотрим слоистую структуру с параметрами: | Рассмотрим слоистую структуру с параметрами: | ||
| − | * Полувысота слоев: | + | * Полувысота слоев: <math>h_1 = h_3 = 2h_2</math> |
| − | * Проводимость слоев: | + | * Проводимость слоев: <math>\kappa_1 = 25 \kappa_2,~\kappa_3 = 2 \kappa_2</math> |
| − | * Полудлина каждого слоя | + | * Полудлина каждого слоя <math>A = 20h_2</math> |
| − | * Радиус кругового отверстия | + | * Радиус кругового отверстия <math>R = 0.5 h_2</math> |
| − | * Количество узлов на контуре отверстия | + | * Количество узлов на контуре отверстия <math>N_s</math> = 90 |
| − | * Количество узлов на границе между слоями | + | * Количество узлов на границе между слоями <math>N</math> = 1024 |
| − | [[Файл:3lay 05R solution.png| | + | [[Файл:3lay 05R solution.png|1600px|thumb|center|Потенциал от кругового отверстия]] |
| + | |||
| + | ==Заключение== | ||
| + | Основные результаты работы можно сформулировать следующим образом: | ||
| + | |||
| + | * Разработан максимально эффективный алгоритм решения задач для слоистых структур. Эффективность алгоритма достигается применением метода прогонки и быстрого преобразования Фурье. | ||
| + | * Для плоских слоистых структур исследована логарифмическая особенность функции Грина. Показано, что наличие логарифма добавляет к функции Грина константу, значение которой может быть получено численно. | ||
| + | * Показано, что использование дискретного преобразования Фурье добавляет к функции Грина константу, значение которой может быть получено аналитически. | ||
| + | * Для определения точности нахождения функции Грина представлены 3 тестовые задачи. На их примере показано, что точность нахождения функции Грина не зависит от числа слоев в рассматриваемой структуре, а зависит от изменяемых параметров. Это позволяет контролировать точность результатов. | ||
| + | * Применение функции Грина для решения краевой задачи показало сильное влияние границ слоев на конечный результат при увеличении размера кругового отверстия | ||
==Список использованной литературы== | ==Список использованной литературы== | ||
Текущая версия на 18:58, 12 июня 2017
МАГИСТЕРСКАЯ РАБОТА
Автор работы: Марков Николай
Научный руководитель: А.М. Линьков
Содержание
Введение[править]
Исследование слоистых структур имеет важное значение для задач теории упругости, механики материалов, теории поля и механики грунтов. Например, учет слоистости горной породы может увеличить точность получаемых результатов при численном моделировании распространения трещины гидроразрыва (ГРП).
Существует два основных подхода к решению задач для слоистых структур. Оба подхода используют геометрическую особенность слоистой структуры: слои представляют собой систему типа цепочки. Первый подход основан на использовании метода матричного переноса и его модификаций. Суть данного метода заключается в переносе значений усилий и смещений (или их линейной комбинации), заданных на границе между слоями, на соседнюю границу. Основной недостаток данного подхода состоит в физической некорректности одновременного переноса значений смещений и усилий, что ведет к низкой обусловленности квадратных матриц, используемых для связи значений на соседних границах. С увеличением числа слоев в рассматриваемой структуре это приводит к неустойчивости решения и увеличению ошибки.
В своих работах Р.М.Раппапорт впервые сводит решение задачи для слоистой структуры к решению трехточечных разностных уравнений. Такой подход позволяет использовать детально изученную теорию разностных уравнений и эффективные численные методы их решения. Для получения связи усилий и смещений на границах слоев в работах Р.М.Раппапорт используется Фурье преобразование.
Подробное сравнение основных методов решения задач для слоистых структур представлено в работе А.М.Линькова и Н.А.Филиппова в которой показано, что наиболее эффективный метод решения состоит в сведении исходной задачи к решению трехточечных разностных уравнений. В качестве численного метода решения предлагается использовать устойчивый и эффективный метод прогонки. В отличие от метода матричного переноса, метод прогонки не теряет устойчивость при увеличении числа слоев.
Особый интерес представляет исследование слоистой среды, содержащей неоднородности. Решение такой задачи можно получить с использованием метода граничных элементов (МГЭ), или метода конечных элементов (МКЭ). Использование МКЭ приводит к ряду сложностей, таких как высокий порядок конечной алгебраической системы, учет точек сингулярностей и разрывов. Применение МКЭ приводит также к трудностям при рассмотрении очень тонких слоев, так как необходимое сгущение сетки приводит к заметному увеличению порядка конечной алгебраической системы.
Наиболее оптимальным методом решения линейных задач для слоистых структур с неоднородностями является метод граничных элементов, включающий в себя нахождение функции Грина для слоистой структуры без неоднородностей. Такой подход позволяет свести решение исходной задачи к решению интегральных уравнений с синугулярными и гиперсингулярными ядрами, заданных только на границах неоднородностей. В результате, порядок конечной алгебраической системы равен суммарному числу узлов на границах неоднородностей.
Цель данной работы состоит в эффективной численной реализации алгоритма решения задач для слоистых структур с неоднородностями, и исследовании его ключевых особенностей. Эффективность численного алгоритма достигается благодаря двум важнейшим факторам:
- Геометрическая особенность слоистой структуры позволяет применять эффективный метод прогонки для нахождения решения. Использование метода прогонки приводит к существенному уменьшению количества операций, необходимых для получения решения( вместо для метода Гаусса.)
- Рассматриваемые уравнения линейные, а границы слоев плоские и параллельные. Эти два условия позволяют применять преобразование Фурье. В численной реализации использование быстрого преобразования Фурье приводит к уменьшению количества операций и времени расчета (вместо проводится только операций).
Большой практический интерес также представляют:
- Точность численного нахождения функции Грина слоистой среды
- Особенности использования дискретного преобразования Фурье
- Исследование логарифмической особенности функции Грина
Постановка задачи[править]
Рассмотрим систему, состоящую из слоев с плоскими параллельными границами. Каждый слой может иметь поры и трещины. Пронумеруем слои снизу вверх от до , а их границы от до . Оси и декартовой системы координат направим вдоль границ слоев в горизонтальной плоскости, а ось -- перпендикулярно вверх по направлению нормали к границам слоев. Величины, относящиеся к -ому слою или контакту будем обозначать индексом . Индексом 't' ('b') будем обозначать значения на верхней (нижней) границе слоя. Тогда для смещений, испытывающих разрыв на -ой границе, . Для системы слоев справедливо уравнение:
где - линейный дифференциальный оператор для -ого слоя. В качестве может использоваться, например, оператор Ляме или оператор Лапласа. Условие равновесия на границах имеет вид:
где -- усилие на -ой границе в направлении оси . Если на границах некоторых пор или трещин заданы усилия , то:
Контактное взаимодействие на -ой границе определяется соотношением:
где - заданная матрица контактного взаимодействия на границе между и слоем. В случае идеального контакта на -ой границе и . На границах пор и трещин задаются неоднородные граничные условия:
где и - заданная симметричная матрица и заданный вектор разрыва смещений на границе пор(трещин) и среды.
Главная задача состоит в нахождении напряжений и смещений в слоистой структуре с неоднородностями.
Метод решения[править]
Метод решения поставленной задачи основан на геометрической особенности системы слоев с плоскими параллельными границами: слои являются системой типа цепочки. Таким образом, исходная задача сводится к решению методом прогонки системы разностных уравнений.
Исходную задачу легко свести к уравнениям, заданным только на поверхностях пор и трещин, если известна функция Грина для слоистой структуры без неоднородностей, удовлетворяющая уравнению:
где -- единичная матрица; -- дельта-функция Дирака. -ый столбец функции Грина есть вектор смещений, полученный в результате действия точечного источника, приложенного в точке в направлении . Таким образом, для решения поставленной задачи необходимо найти функцию Грина для слоистой среды без неоднородностей.
Пример: круговое отверстие в слоистой структуре для оператора Лапласа[править]
Рассмотрим слоистую структуру с параметрами:
- Полувысота слоев:
- Проводимость слоев:
- Полудлина каждого слоя
- Радиус кругового отверстия
- Количество узлов на контуре отверстия = 90
- Количество узлов на границе между слоями = 1024
Заключение[править]
Основные результаты работы можно сформулировать следующим образом:
- Разработан максимально эффективный алгоритм решения задач для слоистых структур. Эффективность алгоритма достигается применением метода прогонки и быстрого преобразования Фурье.
- Для плоских слоистых структур исследована логарифмическая особенность функции Грина. Показано, что наличие логарифма добавляет к функции Грина константу, значение которой может быть получено численно.
- Показано, что использование дискретного преобразования Фурье добавляет к функции Грина константу, значение которой может быть получено аналитически.
- Для определения точности нахождения функции Грина представлены 3 тестовые задачи. На их примере показано, что точность нахождения функции Грина не зависит от числа слоев в рассматриваемой структуре, а зависит от изменяемых параметров. Это позволяет контролировать точность результатов.
- Применение функции Грина для решения краевой задачи показало сильное влияние границ слоев на конечный результат при увеличении размера кругового отверстия
Список использованной литературы[править]
- Aleynikov S.M., Spatial Contact Problems in Geotechnics , Foundations of Engineering Mechanics, 2011.
- Brebbia C.A., Boundary Element Techniques in Computer-Aided Engineering, 1984
- Brebbia C.A., Tells J.C.F., Wrobel L.C., Boundary Element Techniques, Springer, 1984
- Crouch S.L., Starfield A.M., Boundary Element Method in Solid Mechanics, 1983
- Dobroskok A.A., Linkov A.M., Complex variable equations and the numerica solution of harmonic problems for piecewise-homogeneous media, Journal of Applied Mathematics and Mechanics, 73 (2009) 313-325
- Filippov N.A., Linkov A.M., Milova L.A., Zoubkov V.V., A Method to Calculate Stresses and Deformations in 3D Layered Strata, Advances in Rock Mechanics, 1998
- Linkov A.M., Filippov N.A., Difference Equations Approach to the Analysis of Layered Systems, Meccanica, 26:195-209
- Linkov A.M., Linkova A.A., Savitski A.A., An Effective Method for Multi-Layered Media with Cracks and Cavities, International Journal of Damage Mechanics, 1994.
- Linkov A.M. Boundary Integral Equations in Elasticity Theory, SOLID MECHANICS AND ITS APPLICATIONS, Vol.99, 2002
- Maier G., Novati G., On boundary element-transfer matrix analysis of layered elastic systems, 7th Intrnat. Conf. on Boundary Elements in Engineering, Como (Italy), pp. 1-28, 1985.
- Novati G., On the analysis of elastic layers by a Fourier series, Green's function approach, Atti Accad. Naz. Lincei, 293-304, 1987.
- Ruppoport R.M., To the question of finding the solution of axisymmetric and plane elasticity problems for multilayered media, Proc. Hydrotechnical Institute, Leningrad, 1963.
- Ruppoport R.M., To the question of finding the solution for displacements of three-dimensional elasticity problem for multilayered half-space, Proc. Hydrotechnical Institute, Leningrad, 1966.
- Вигдерович И.Е., Ламзюк В.Д., Приварников А.К., Об использовании метода функций податливости при решении граничных задач для многослойных оснований, 1979.
- Годунов С.К., Рябенький В.С., Разностные схемы: введение в теорию, Наука, 1977
- Никишин В.С., Шапиро Г.С., Пространственные задачи теории упругости для многослойных сред, 1970.
- Оболашвили Е.И., Преобразование Фурье и его применения в теории упругости , Тбилиси, Мецниереба, 1979.
- Самарский А.А., Гулин А.В., Численные методы, Наука, Москва, 1989.
- Самарский А.А., Николаев Е.С., Методы решения сеточных уравнений, Наука, Москва, 1978.
- Шевляков Ю.А., Матричные алгоритмы в теории упругости неоднородных сред, 1977.