Моделирование дерева Пифагора — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
(→top) |
|||
| (не показаны 4 промежуточные версии 1 участника) | |||
| Строка 1: | Строка 1: | ||
| − | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Serov_A_S/interface.html |width=1050 |height= | + | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Serov_A_S/derevo/interface.html |width=1050 |height=540 |border=0 }} |
| + | |||
== Что такое Дерево Пифагора? == | == Что такое Дерево Пифагора? == | ||
'''Дерево Пифагора''' — разновидность фрактала, основанная на фигуре, известной как «[https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%9F%D0%B8%D1%84%D0%B0%D0%B3%D0%BE%D1%80%D0%B0#.D0.94.D0.BE.D0.BA.D0.B0.D0.B7.D0.B0.D1.82.D0.B5.D0.BB.D1.8C.D1.81.D1.82.D0.B2.D0.BE_.D0.95.D0.B2.D0.BA.D0.BB.D0.B8.D0.B4.D0.B0 Пифагоровы штаны]». | '''Дерево Пифагора''' — разновидность фрактала, основанная на фигуре, известной как «[https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%9F%D0%B8%D1%84%D0%B0%D0%B3%D0%BE%D1%80%D0%B0#.D0.94.D0.BE.D0.BA.D0.B0.D0.B7.D0.B0.D1.82.D0.B5.D0.BB.D1.8C.D1.81.D1.82.D0.B2.D0.BE_.D0.95.D0.B2.D0.BA.D0.BB.D0.B8.D0.B4.D0.B0 Пифагоровы штаны]». | ||
| Строка 5: | Строка 6: | ||
== Особенности == | == Особенности == | ||
Одним из свойств дерева Пифагора является то, что если площадь первого прямоугольника равна единице, то на каждом уровне сумма площадей прямоугольников тоже будет равна единице. | Одним из свойств дерева Пифагора является то, что если площадь первого прямоугольника равна единице, то на каждом уровне сумма площадей прямоугольников тоже будет равна единице. | ||
| + | |||
== Разновидности == | == Разновидности == | ||
| + | |||
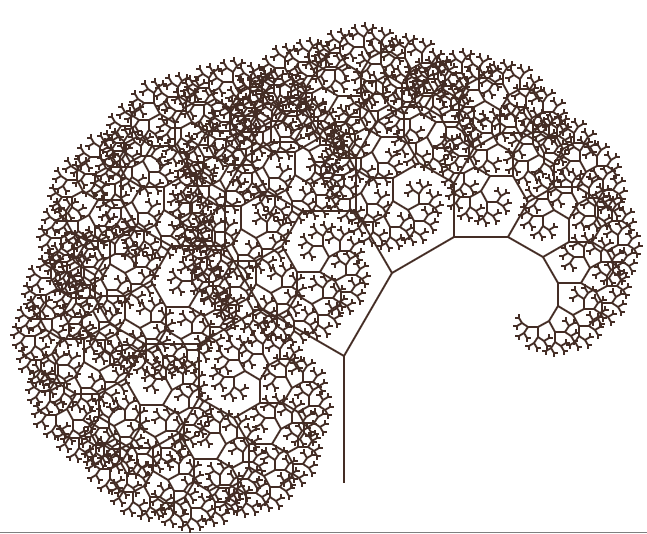
| + | Если изображать только отрезки, соединяющие каким-либо образом выбранные «центры» фигур, то получается обнаженное дерево Пифагора. | ||
| + | [[File:derevo.PNG]] | ||
| + | |||
Если в классическом дереве Пифагора угол между фигурами равен 45 градусам, то также можно построить и обобщённое дерево Пифагора при использовании других углов. Такое дерево часто называют обдуваемое ветром дерево Пифагора. | Если в классическом дереве Пифагора угол между фигурами равен 45 градусам, то также можно построить и обобщённое дерево Пифагора при использовании других углов. Такое дерево часто называют обдуваемое ветром дерево Пифагора. | ||
| − | + | [[File:derevo1.PNG]] | |
| − | |||
Текущая версия на 16:07, 15 июня 2017
Что такое Дерево Пифагора?[править]
Дерево Пифагора — разновидность фрактала, основанная на фигуре, известной как «Пифагоровы штаны».
Особенности[править]
Одним из свойств дерева Пифагора является то, что если площадь первого прямоугольника равна единице, то на каждом уровне сумма площадей прямоугольников тоже будет равна единице.
Разновидности[править]
Если изображать только отрезки, соединяющие каким-либо образом выбранные «центры» фигур, то получается обнаженное дерево Пифагора.
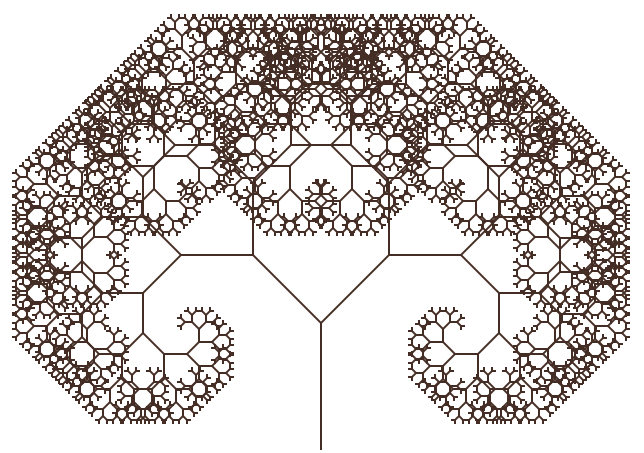
Если в классическом дереве Пифагора угол между фигурами равен 45 градусам, то также можно построить и обобщённое дерево Пифагора при использовании других углов. Такое дерево часто называют обдуваемое ветром дерево Пифагора.