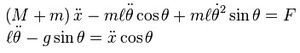Обратный маятник — различия между версиями
Test (обсуждение | вклад) |
(→Модель) |
||
| (не показано 20 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | [[Файл: | + | [[Файл:Inverted_pendulum.png |thumb|250px|right|Обратный маятник на подвижной платформе]] |
===Цель проекта=== | ===Цель проекта=== | ||
| Строка 9: | Строка 9: | ||
* [[Поцелуев Павел|Поцелуев Павел]] (разработка алгоритмов балансировки) | * [[Поцелуев Павел|Поцелуев Павел]] (разработка алгоритмов балансировки) | ||
| − | === | + | ===Модель=== |
Аналитически обратный маятник описывается следующей системой дифференциальных уравнений | Аналитически обратный маятник описывается следующей системой дифференциальных уравнений | ||
[[Файл:Inverted_pendulum_2.jpg|300px|none]] | [[Файл:Inverted_pendulum_2.jpg|300px|none]] | ||
| − | Для изучения обратного маятника была разработана модель в системе Matlab Simulink. На данный момент в модели реализован алгоритм балансировки с помощью ПИД-регуляторов. | + | Для изучения обратного маятника была разработана модель в системе Matlab Simulink. На данный момент в модели реализован алгоритм балансировки с помощью отдельных ПИД-регуляторов для контроля за устойчивостью маятника и положением каретки. |
| + | На рисунке представлена реализация модели в программном пакете simulink. | ||
| + | В схему добавлено запаздывающее звено, которое эмитирует задержку в управлении, вызванной скоростью работы контроллера. | ||
| + | [[File:TSxame.png|600px|none]] | ||
| + | Можно загрузить [[Media:Pendulum4.zip|модель для simulink]] | ||
| + | |||
| + | ===Нахождение коэффициентов регулятора методом подбора=== | ||
| + | Сначала подбирается коэффициент Kp с тем, чтобы системы выходила на предел устойчивости, | ||
| + | как только значение получено, от него берётся 0,6 и вычисляются остальные значения коэффициентов регулятора. | ||
| + | |||
| + | ===Нахождение коэффициентов регулятора по методу Зиглера и Никольса=== | ||
| + | подробно метод изложен на странице 88 документа http://www.cta.ru/cms/f/374303.pdf | ||
| + | система должна быть устойчивой, поэтому сначала коэффициенты подбираются для маятника в нижнем положении | ||
| + | находим коэффициенты a=11.5 L=0.13 T = 0.5c | ||
| + | пользуемся формулой [[File:Image266.gif|none]] находим K_p = 26 отклик на воздействие | ||
| + | [[File:Founda pend.png|400px|none]] | ||
| + | ===Пример сохранения устойчивости=== | ||
| + | Пример сохранения устойчивости, при отклонении маятника на 10 градусов от вертикали. | ||
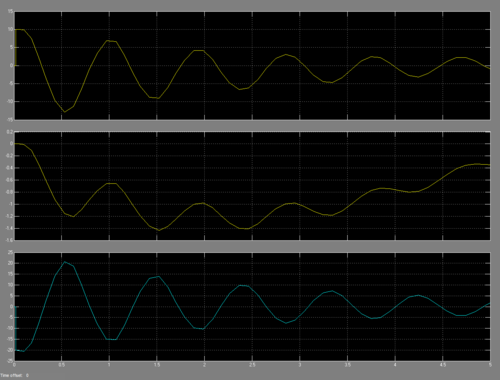
| + | [[Изображение:PictOfbalance.png|thumb|500px|center|верхний график--угол отклонения от вертикали. средний положение каретки, нижний-- приложенная сила, Н]] | ||
| + | |||
| + | ===Нахождение коэффициентов регулятора с помощью генетического ралгоритма=== | ||
| + | Был реализован алгоритм автоматической настройки ПИД-регулятора с помощью генетических алгоритмов (использовался toolbox gatool в системе Matlab). По [[Медиа:Inverted_pendulum_project.zip|ссылке]] можно скачать архив с файлами, необходимыми для экспериментов с моделью. | ||
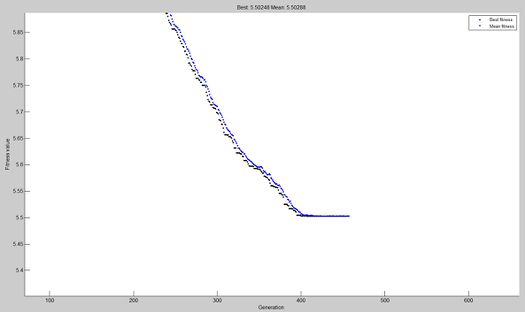
Ниже на видео показана реакция системы (с настроенными ПИД-регуляторами) на приложенный импульс, справа изображен график сходимости генетического алгоритма | Ниже на видео показана реакция системы (с настроенными ПИД-регуляторами) на приложенный импульс, справа изображен график сходимости генетического алгоритма | ||
| − | [[Файл: | + | |
| + | [[Файл:Inverted pendulum plot.jpg|thumb|525px|right|график сходимости]] | ||
{{#widget:Iframe | {{#widget:Iframe | ||
|url=http://www.youtube.com/embed/7XpFwX1iFn4?rel=0&hd=1 | |url=http://www.youtube.com/embed/7XpFwX1iFn4?rel=0&hd=1 | ||
| Строка 22: | Строка 44: | ||
|border=0 | |border=0 | ||
}} | }} | ||
| − | |||
===Планы развития проекта=== | ===Планы развития проекта=== | ||
| Строка 29: | Строка 50: | ||
== Ссылки == | == Ссылки == | ||
| − | * [https://ru.wikipedia.org/wiki/%D0%9E%D0%B1%D1%80%D0%B0%D1%82%D0%BD%D1%8B%D0%B9_%D0%BC%D0%B0%D1%8F%D1%82%D0%BD%D0%B8%D0%BA Обратный маятник] | + | * [https://ru.wikipedia.org/wiki/%D0%9E%D0%B1%D1%80%D0%B0%D1%82%D0%BD%D1%8B%D0%B9_%D0%BC%D0%B0%D1%8F%D1%82%D0%BD%D0%B8%D0%BA Обратный маятник]+ |
| + | * [http://www.cta.ru/cms/f/374303.pdf ПИД-регуляторы:вопросы реализации] | ||
| + | * [http://www.bookasutp.ru/Chapter5_1_4.aspx Идентификация в замкнутом и разомкнутом контуре] | ||
Текущая версия на 17:59, 27 ноября 2015
Содержание
- 1 Цель проекта
- 2 Проектная команда
- 3 Модель
- 4 Нахождение коэффициентов регулятора методом подбора
- 5 Нахождение коэффициентов регулятора по методу Зиглера и Никольса
- 6 Пример сохранения устойчивости
- 7 Нахождение коэффициентов регулятора с помощью генетического ралгоритма
- 8 Планы развития проекта
- 9 Ссылки
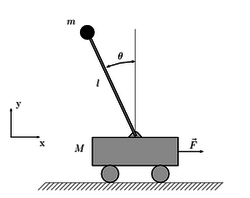
Цель проекта[править]
Написание ряда алгоритмов для балансировки обратного маятника
Проектная команда[править]
- Руководитель проекта - Лобода Ольга Сергеевна
- Опочанский Александр (разработка модели обратного маятника)
- Поцелуев Павел (разработка алгоритмов балансировки)
Модель[править]
Аналитически обратный маятник описывается следующей системой дифференциальных уравнений
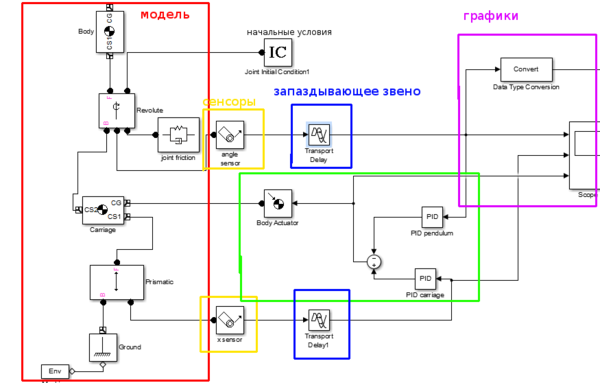
Для изучения обратного маятника была разработана модель в системе Matlab Simulink. На данный момент в модели реализован алгоритм балансировки с помощью отдельных ПИД-регуляторов для контроля за устойчивостью маятника и положением каретки. На рисунке представлена реализация модели в программном пакете simulink. В схему добавлено запаздывающее звено, которое эмитирует задержку в управлении, вызванной скоростью работы контроллера.
Можно загрузить модель для simulink
Нахождение коэффициентов регулятора методом подбора[править]
Сначала подбирается коэффициент Kp с тем, чтобы системы выходила на предел устойчивости, как только значение получено, от него берётся 0,6 и вычисляются остальные значения коэффициентов регулятора.
Нахождение коэффициентов регулятора по методу Зиглера и Никольса[править]
подробно метод изложен на странице 88 документа http://www.cta.ru/cms/f/374303.pdf система должна быть устойчивой, поэтому сначала коэффициенты подбираются для маятника в нижнем положении находим коэффициенты a=11.5 L=0.13 T = 0.5c
пользуемся формулой находим K_p = 26 отклик на воздействиеПример сохранения устойчивости[править]
Пример сохранения устойчивости, при отклонении маятника на 10 градусов от вертикали.
Нахождение коэффициентов регулятора с помощью генетического ралгоритма[править]
Был реализован алгоритм автоматической настройки ПИД-регулятора с помощью генетических алгоритмов (использовался toolbox gatool в системе Matlab). По ссылке можно скачать архив с файлами, необходимыми для экспериментов с моделью.
Ниже на видео показана реакция системы (с настроенными ПИД-регуляторами) на приложенный импульс, справа изображен график сходимости генетического алгоритма
Планы развития проекта[править]
- Нами также был реализован нейроэволюционный алгоритм на языке Java. В будущем планируется применить его для балансировки обратного маятника (возможно, для этого понадобится реализовать модель маятника на Java) и провести сравнительный анализ различных алгоритмов балансировки
- Реализовать модель обратного маятника в Fablab Политех, проверить работу различных алгоритмов на практике