Соколов Алексей. "Динамика несферических частиц" — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
(→Динамические уравнения :) |
|||
| (не показано 11 промежуточных версий 3 участников) | |||
| Строка 4: | Строка 4: | ||
==Задание характеристик частиц== | ==Задание характеристик частиц== | ||
| − | Каждая частица имеет радиус вектор и пару ортогональных векторов. Таким образом | + | Каждая частица имеет радиус вектор и пару ортогональных векторов. Таким образом определяем положение углов. |
==Детектирование столкновений== | ==Детектирование столкновений== | ||
Идея метода состоит в том, чтобы переходить в систему отсчета одной из частиц, и проверять, находятся ли углы внутри частицы | Идея метода состоит в том, чтобы переходить в систему отсчета одной из частиц, и проверять, находятся ли углы внутри частицы | ||
| − | [[Файл: | + | [[Файл:Detec.PNG |300 px|Детектирование столкновений]] |
Т.о. если выполняется условие | Т.о. если выполняется условие | ||
| Строка 20: | Строка 20: | ||
<math>\vec{F} = kl\vec{n}</math>, где <math>\vec{n}</math> - нормаль к поверхности | <math>\vec{F} = kl\vec{n}</math>, где <math>\vec{n}</math> - нормаль к поверхности | ||
| − | ==== Динамические уравнения | + | ==== Динамические уравнения ==== |
| + | <math>\left\{ | ||
| + | \begin{array}{rcl} | ||
| + | m \frac{d^2 \vec{r}}{dt^2} & = & \sum^{n}_{j=1} {\vec{F}}_{\j} \\ | ||
| + | &\\ | ||
| + | J \frac{d^2\vec{w}}{dt^2} & = & \sum^{m}_{i=1} {\vec{M}}_{\i} \\ | ||
| + | |||
| + | \end{array} | ||
| + | \right. </math> | ||
| − | + | ==== Leapfrog интегрирование ==== | |
| − | == | + | <math>\left\{ |
| + | \begin{array}{rcl} | ||
| + | \vec{v}_{i+1} & = & \vec{v}_i + \vec{a}_i\Delta t \\ | ||
| + | &\\ | ||
| + | \vec{r}_{i+1} & = & \vec{r}_i + \vec{v}_{i+1}\Delta t \\ | ||
| + | |||
| + | \end{array} | ||
| + | \right. </math> | ||
| − | [[Файл: | + | ==Диссипативная модель== |
| + | |||
| + | [[Файл: dissipative_forces.png |500 px|диссипативная модель]] | ||
| + | |||
| + | <br>, где <math> k_{1}, k_{2}</math> - коэффициенты упругости <br> <math> \beta </math> - коэффициент вязкого трения <br> <math> \mu </math> - коэффициент сухого трения | ||
| + | |||
| + | == См. также == | ||
| + | |||
| + | *[[Соколов Алексей]] | ||
[[Category: Студенческие проекты]] | [[Category: Студенческие проекты]] | ||
| + | [[Category: Механика дискретных сред]] | ||
| + | |||
| + | [[Category: Личные страницы]] | ||
Текущая версия на 17:39, 29 мая 2014
Модель взаимодействия квадратных частиц в 2D
Содержание
Задание характеристик частиц[править]
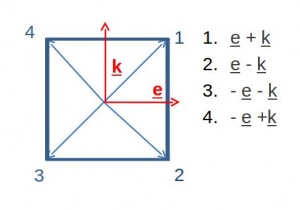
Каждая частица имеет радиус вектор и пару ортогональных векторов. Таким образом определяем положение углов.
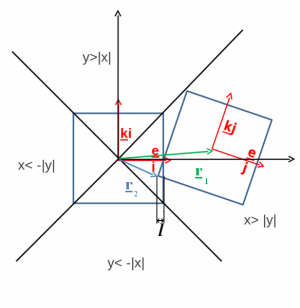
Детектирование столкновений[править]
Идея метода состоит в том, чтобы переходить в систему отсчета одной из частиц, и проверять, находятся ли углы внутри частицы
Т.о. если выполняется условие
то частицы находятся в контакте.
Упругие силы и моменты[править]
, где - нормаль к поверхности
Динамические уравнения[править]
Leapfrog интегрирование[править]
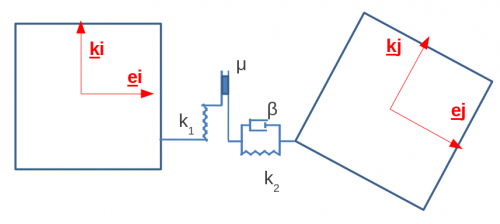
Диссипативная модель[править]
, где - коэффициенты упругости
- коэффициент вязкого трения
- коэффициент сухого трения