Отражение волн от стыка двух цепочек — различия между версиями
(→Алгоритм программы) |
|||
| (не показано 13 промежуточных версий этого же участника) | |||
| Строка 7: | Строка 7: | ||
'''Семестр:''' осень 2018 | '''Семестр:''' осень 2018 | ||
| + | ==Постановка задачи== | ||
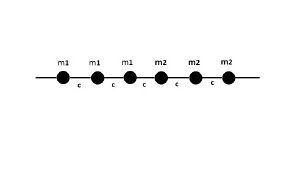
| − | = | + | Рассматриваются две одномерные цепочки с частицами разной массы, соединенные между собой. В свою очередь, частицы соединены пружинами с жесткостью С, массы частиц связаны через числовой параметр <math> n =\frac{m_{2}}{m_{1}} </math>. |
| − | + | [[File:Chain diif mass.jpg|thumb]] | |
==Решение задачи== | ==Решение задачи== | ||
| Строка 20: | Строка 21: | ||
</math><br /> | </math><br /> | ||
| + | На стыке двух цепочек вследствие разности масс возникает отраженная волна, чьё движение также описывается уравнением движения частиц в одномерной цепочке. | ||
| + | |||
| + | Для решения данного уравнения использовался [https://ru.wikipedia.org/wiki/%D0%98%D0%BD%D1%82%D0%B5%D0%B3%D1%80%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%92%D0%B5%D1%80%D0%BB%D0%B5 метод численного интегрирования Верле], так как он более устойчив, чем, например, более простой метод Эйлера, и имеет при этом другие качества, необходимые для моделирования физических процессов в реальном времени, а также позволяет накладывать на систему точек различные ограничения. | ||
| + | |||
| + | ==Алгоритм программы== | ||
| + | |||
| + | На первую частицу действует заданная сила <math> F = F_{0} Sin( \omega t) </math>. Таким образом, можно найти скорость и перемещение первой частицы. Зная перемещение первой частицы, можно рассчитать перемещения остальных частиц. | ||
| + | |||
| + | Пользователь может менять количество частиц, частоту колебания и параметр, связывающий массы частиц. | ||
| − | + | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Timoshenko/Wave/Kurs1.html |width=1200 |height=600 |border=0 }} | |
| + | |||
| + | =Выводы= | ||
| + | |||
| + | Таким образом, в ходе решения задачи были найдены перемещения частиц в обеих цепочках и построен соответствующий график. | ||
| + | |||
| + | Планируется получить значения кинетической, потенциальной и полной энергий и построение соответствующих графиков, а также расширение возможностей пользователя задавать интересующие параметры. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | =Ссылки= | ||
| − | + | *[[Кафедра "Теоретическая механика"]] | |
| − | + | *[[Курсовые работы по ВМДС: 2018-2019]] | |
| − | * | + | *[[Введение в механику дискретных сред]] |
| − | * | ||
| − | * | ||
| − | |||
Текущая версия на 00:58, 29 января 2019
Курсовой проект по Механике дискретных сред
Исполнитель: Тимошенко Валентина
Группа: 43604/1
Семестр: осень 2018
Постановка задачи[править]
Рассматриваются две одномерные цепочки с частицами разной массы, соединенные между собой. В свою очередь, частицы соединены пружинами с жесткостью С, массы частиц связаны через числовой параметр .
Решение задачи[править]
Движение частиц в одномерной цепочке описывается следующим дифференциальным уравнением.
На стыке двух цепочек вследствие разности масс возникает отраженная волна, чьё движение также описывается уравнением движения частиц в одномерной цепочке.
Для решения данного уравнения использовался метод численного интегрирования Верле, так как он более устойчив, чем, например, более простой метод Эйлера, и имеет при этом другие качества, необходимые для моделирования физических процессов в реальном времени, а также позволяет накладывать на систему точек различные ограничения.
Алгоритм программы[править]
На первую частицу действует заданная сила . Таким образом, можно найти скорость и перемещение первой частицы. Зная перемещение первой частицы, можно рассчитать перемещения остальных частиц.
Пользователь может менять количество частиц, частоту колебания и параметр, связывающий массы частиц.
Выводы[править]
Таким образом, в ходе решения задачи были найдены перемещения частиц в обеих цепочках и построен соответствующий график.
Планируется получить значения кинетической, потенциальной и полной энергий и построение соответствующих графиков, а также расширение возможностей пользователя задавать интересующие параметры.