Отражение волн от стыка двух цепочек

Курсовой проект по Механике дискретных сред

Исполнитель: Тимошенко Валентина

Группа: 43604/1

Семестр: осень 2018

Постановка задачи

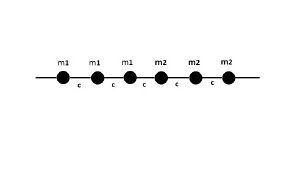
Рассматриваются две одномерные цепочки с частицами разной массы, соединенные между собой. В свою очередь, частицы соединены пружинами с жесткостью С, массы частиц связаны через числовой параметр [math] n =\frac{m_{2}}{m_{1}} [/math].

Решение задачи

Движение частиц в одномерной цепочке описывается следующим дифференциальным уравнением.

[math] m\frac{d^2 u_{n}}{dt^2}=c(u_{n+1}-2u_{n}+u_{n-1}) [/math]

На стыке двух цепочек вследствие разности масс возникает отраженная волна, чьё движение также описывается уравнением движения частиц в одномерной цепочке.

Для решения данного уравнения использовался метод численного интегрирования Верле, так как он более устойчив, чем, например, более простой метод Эйлера, и имеет при этом другие качества, необходимые для моделирования физических процессов в реальном времени, а также позволяет накладывать на систему точек различные ограничения.

Алгоритм программы

На первую частицу действует заданная сила [math] F = F_{0} Sin( \omega t) [/math]. Таким образом, можно найти скорость и перемещение первой частицы. Зная перемещение первой частицы, можно рассчитать перемещения остальных частиц.

Пользователь может менять количество частиц, частоту колебания и параметр, связывающий массы частиц.

Выводы

Таким образом, в ходе решения задачи были найдены перемещения частиц в обеих цепочках и построен соответствующий график.

Планируется получить значения кинетической, потенциальной и полной энергий и построение соответствующих графиков, а также расширение возможностей пользователя задавать интересующие параметры.

Ссылки

• Кафедра "Теоретическая механика"
• Курсовые работы по ВМДС: 2018-2019
• Введение в механику дискретных сред