Particles chain with V-model interaction — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
 
(не показана 1 промежуточная версия этого же участника)
Строка 1: Строка 1:
 +
[[ru:Цепочка частиц с V-model взаимодействием]]
 
[[The virtual laboratory]] > [[Particles chain with V-model interaction]] <HR>
 
[[The virtual laboratory]] > [[Particles chain with V-model interaction]] <HR>
  
Строка 6: Строка 7:
  
 
The model is described by the following formulas:
 
The model is described by the following formulas:
−
[[Файл:Fig2_single_bond.png|350px|thumb|right| Interaction of two particles]]  
+
[[File:Fig2_single_bond.png|350px|thumb|right| Interaction of two particles]]  
 
Interaction force:
 
Interaction force:
  
Строка 24: Строка 25:
 
== Description of realization of a chain ==  
 
== Description of realization of a chain ==  
  
−
[[Файл: Fig3_bond_def.png|600px|thumb|right|Types of deformations]]
+
[[File: Fig3_bond_def.png|600px|thumb|right|Types of deformations]]
  
 
In the program three various boundary conditions which can are realized chosen as the user:
 
In the program three various boundary conditions which can are realized chosen as the user:
Строка 66: Строка 67:
  
 
<div class="mw-collapsible-content">
 
<div class="mw-collapsible-content">
−
Файл '''"V-model.js"'''
+
File '''"V-model.js"'''
 
<syntaxhighlight lang="javascript" line start="1" enclose="div">
 
<syntaxhighlight lang="javascript" line start="1" enclose="div">
 
function MainParticle(canvas) {
 
function MainParticle(canvas) {
−
     // Предварительные установки
+
     // Presets
−
     var context    = canvas.getContext("2d");  // на context происходит рисование
+
     var context    = canvas.getContext("2d");  // on context drawing takes place
 
 
−
   //  Задание констант
+
   //  Specifying constants
−
     const Pi = 3.1415926;                  // число "пи"
+
     const Pi = 3.1415926;                  // "Pi"
−
     const m0 = 1;                          // масштаб массы
+
     const m0 = 1;                          // weight scale
−
     const T0 = 1;                          // масштаб времени (период колебаний исходной системы)
+
     const T0 = 1;                          // time scale (the period of oscillation of the original system )
−
     const a0 = 1;                          // масштаб расстояния (диаметр шара)
+
     const a0 = 1;                          // distance scale ( ball diameter)
−
     const g0 = a0 / T0 / T0;                // масштаб ускорения (ускорение, при котором за T0 будет пройдено расстояние a0)
+
     const g0 = a0 / T0 / T0;                // accelerating the scale (acceleration , in which for T0 be completed distance a0)
−
     const k0 = 2 * Pi / T0;                // масштаб частоты
+
     const k0 = 2 * Pi / T0;                // frequency scale
−
     //const C0 = m0 * k0 * k0;                // масштаб жесткости
+
     //const C0 = m0 * k0 * k0;                // hardness scale
 
     const C0 = 1;
 
     const C0 = 1;
−
     const B0 = 2 * m0 * k0;                // масштаб вязкости
+
     const B0 = 2 * m0 * k0;                // viscosity scale
  
−
     // *** Задание физических параметров ***
+
     // *** Setting physical parameters ***
  
−
     const Ny = 5;                          // число шаров, помещающихся по вертикали в окно (задает размер шара относительно размера окна)
+
     const Ny = 5;                          // the number of balls is placed vertically in a window ( sets the size of the ball relative to the window size )
 
     const Nx = 5;
 
     const Nx = 5;
−
const m = 1 * m0;                      // масса
+
const m = 1 * m0;                      // weight
−
     const Cwall = 10 * C0;                  // жесткость стен
+
     const Cwall = 10 * C0;                  // wall stiffness
−
     //const B = 0.01 * B0;  // вязкость среды
+
     //const B = 0.01 * B0;  // viscosity of the environment
 
     const B = 0;
 
     const B = 0;
−
     const B1 = 0.03 * B0;                  // вязкость на стенках
+
     const B1 = 0.03 * B0;                  // viscosity on the walls
 
     //const B1 = 0;
 
     //const B1 = 0;
−
     //var mg = 0.25 * m * g0;              // сила тяжести
+
     //var mg = 0.25 * m * g0;              // gravity
−
     const r = 0.5 * a0;                    // радиус частицы в расчетных координатах
+
     const r = 0.5 * a0;                    // the radius of the particles in the calculated coordinates
−
var stiff = 1 * C0;                    // "жесткость" пружинки
+
var stiff = 1 * C0;                    // "Rigidity" of a spring
  
 
var vx0 = 0 * a0/T0;
 
var vx0 = 0 * a0/T0;
Строка 101: Строка 102:
 
     //Text_vx0.value  = vx0;
 
     //Text_vx0.value  = vx0;
 
 
−
     // *** Параметры системы ***
+
     // *** System settings ***
−
var c = 1;// жесткость
+
var c = 1;// rigidity
−
var n = 10;// количество частиц
+
var n = 10;// the amount of particles
 
var c_a = 100//1;//longitudinal
 
var c_a = 100//1;//longitudinal
 
var c_d = 100//c_a*1;//shear
 
var c_d = 100//c_a*1;//shear
Строка 110: Строка 111:
 
var J = 1;
 
var J = 1;
 
var m_0 = 1.5;
 
var m_0 = 1.5;
−
var f = 0 ;//вариант либо свободное тело, либо закрепелнный край
+
var f = 0 ;//option or free body or fixed edge
 
var ugol = 0;
 
var ugol = 0;
 
var sm_x = 0;
 
var sm_x = 0;
Строка 116: Строка 117:
 
 
 
 
−
     // *** Задание вычислительных параметров ***
+
     // *** Setting the parameters of computing ***
  
−
     const fps = 50;                        // frames per second - число кадров в секунду (качеcтво отображения)50
+
     const fps = 50;                        // frames per second - the number of frames per second ( kachectvo display )50
−
     const spf = 10;//5;                        // steps per frame  - число шагов интегрирования между кадрами (скорость расчета)
+
     const spf = 10;//5;                        // steps per frame  - the number of integration steps between frames ( calculation speed)
−
     const dt  = 1 * T0 / fps;          // шаг интегрирования
+
     const dt  = 1 * T0 / fps;          // the integration step
 
 
−
// Задание констант для рисования
+
// Setting constants for drawing
−
const scale    =100* canvas.height / Ny / a0;  // масштабный коэффициент для перехода от расчетных к экранным координатам
+
const scale    =100* canvas.height / Ny / a0;  // a scaling factor for the transition from design to screen coordinates
 
 
−
     var w = canvas.width / scale;          // ширина окна в расчетных координатах
+
     var w = canvas.width / scale;          // width of the window in the calculated coordinates
−
     var h = canvas.height / scale;          // высота окна в расчетных координатах
+
     var h = canvas.height / scale;          // window height in calculated coordinates
 
var k1v; var k2v; var k3v; var k4v; var k1x;  var k2x; var k3x; var k4x;  
 
var k1v; var k2v; var k3v; var k4v; var k1x;  var k2x; var k3x; var k4x;  
 
var T1;var T2; var T1_; var T2_;
 
var T1;var T2; var T1_; var T2_;
Строка 138: Строка 139:
 
var B_3 = c_b - B_2/4 - B_4/2;
 
var B_3 = c_b - B_2/4 - B_4/2;
 
 
−
     // -------------------------------        Выполнение программы             ------------------------------------------
+
     // -------------------------------        Implementation of the program             ------------------------------------------
−
// Добавление шара
+
// Addition of a sphere
−
balls=[]//массив содержащий частицы
+
balls=[]//the massif containing particles
 
j=1;
 
j=1;
 
for (i = 0;i<n/2;i++)
 
for (i = 0;i<n/2;i++)
Строка 147: Строка 148:
 
var b1 = [];
 
var b1 = [];
 
var time = 1;
 
var time = 1;
−
b.fi_x = 0*j; //угол с осью ОХ
+
b.fi_x = 0*j; //corner with an axis OX
−
b.omega=0;//угловая скорость
+
b.omega=0;// angular velocity
−
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//смещение для рисования.  
+
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing.  
 
j=j*(-1);
 
j=j*(-1);
−
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;    // расчетные координаты шара
+
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;    // calculated coordinates of a sphere
 
b.Fx=0;b.Fy=0;
 
b.Fx=0;b.Fy=0;
 
b.x_ = b.x;              b.y_  = b.y;  
 
b.x_ = b.x;              b.y_  = b.y;  
−
b.fx = 0;                b.fy  = 0;      // сила, действующая на шар
+
b.fx = 0;                b.fy  = 0;      // force operating on a spher
−
b.vx = vx0;              b.vy  = vy0;      // начальная скорость
+
b.vx = vx0;              b.vy  = vy0;      // initial velocity
−
b1.fi_x = 0*j; //угол с осью ОХ
+
b1.fi_x = 0*j; //corner with an axis OX
 
b1.omega=0;
 
b1.omega=0;
 
b1.Fx=0;b1.Fy=0;
 
b1.Fx=0;b1.Fy=0;
−
b1.x = (w / 2)+diag*(2*i+1)*1.0;          b1.y = h / 2 ;    // расчетные координаты шара
+
b1.x = (w / 2)+diag*(2*i+1)*1.0;          b1.y = h / 2 ;    // calculated coordinates of a sphere
 
b1.x_ = b.x;              b1.y_  = b.y;  
 
b1.x_ = b.x;              b1.y_  = b.y;  
−
b1.fx = 0;                b1.fy  = 0;      // сила, действующая на шар
+
b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
−
b1.vx = vx0;              b1.vy  = vy0;      // начальная скорость
+
b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2+(i)] = b1;//[2*i+1]
 
balls[n/2+(i)] = b1;//[2*i+1]
 
 
 
}
 
}
−
// Основной цикл программы
+
// Basis cycle of the program
−
setInterval(control, 1500 / fps);  // функция control вызывается с периодом, определяемым вторым параметром
+
setInterval(control, 1500 / fps);  // function control is caused with the period determined by the second parameter
 
 
 
// ---------------------------------------------------------------------------------------------------------------------
 
// ---------------------------------------------------------------------------------------------------------------------
−
// ---------------------------------          Определение всех функций             -----------------------------------
+
// ---------------------------------          Definition of all functions             -----------------------------------
 
// ---------------------------------------------------------------------------------------------------------------------
 
// ---------------------------------------------------------------------------------------------------------------------
 
 
−
// основная функция, вызываемая в программе
+
// the trial function caused in the program
 
function control()  
 
function control()  
 
{
 
{
−
         physics(); // делаем spf шагов интегрирование
+
         physics(); // we do spf of steps an integration
−
         draw();    // рисуем частицу
+
         draw();    // we draw a particle
 
}
 
}
−
//=======================новое задание начального состояния
+
//=======================new task of a reference state
−
function rebild()//новое задание начального состояния
+
function rebild()//new task of a reference state
 
{
 
{
 
time = 1;
 
time = 1;
Строка 194: Строка 195:
 
var b1 = [];
 
var b1 = [];
 
var time = 1;
 
var time = 1;
−
b.fi_x = 0*j; //угол с осью ОХ
+
b.fi_x = 0*j; //corner with an axis ОХ
−
b.omega=0;//угловая скорость
+
b.omega=0;//angular velocity
−
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//смещение для рисования.  
+
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing.  
 
j=j*(-1);
 
j=j*(-1);
−
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;    // расчетные координаты шара
+
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;    // calculated coordinates of a sphere
 
b.Fx=0;b.Fy=0;
 
b.Fx=0;b.Fy=0;
 
b.x_ = b.x;              b.y_  = b.y;  
 
b.x_ = b.x;              b.y_  = b.y;  
−
b.fx = 0;                b.fy  = 0;      // сила, действующая на шар
+
b.fx = 0;                b.fy  = 0;      // force operating on a sphere
−
b.vx = vx0;              b.vy  = vy0;      // начальная скорость
+
b.vx = vx0;              b.vy  = vy0;      // initial velocity
−
b1.fi_x = 0*j; //угол с осью ОХ
+
b1.fi_x = 0*j; //corner with an axis ОХ
 
b1.omega=0;
 
b1.omega=0;
 
b1.Fx=0;b1.Fy=0;
 
b1.Fx=0;b1.Fy=0;
−
b1.x = (w / 2)+diag*(2*i+1)*1.0;          b1.y = h / 2 ;    // расчетные координаты шара
+
b1.x = (w / 2)+diag*(2*i+1)*1.0;          b1.y = h / 2 ;    // calculated coordinates of a sphere
 
b1.x_ = b.x;              b1.y_  = b.y;  
 
b1.x_ = b.x;              b1.y_  = b.y;  
−
b1.fx = 0;                b1.fy  = 0;      // сила, действующая на шар
+
b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
−
b1.vx = vx0;              b1.vy  = vy0;      // начальная скорость
+
b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2+(i)] = b1;//[2*i+1]
 
balls[n/2+(i)] = b1;//[2*i+1]
Строка 216: Строка 217:
 
context.clearRect(0, 0, w * scale, h * scale);  
 
context.clearRect(0, 0, w * scale, h * scale);  
 
}
 
}
−
//=======================Выбор типа задачи======================
+
//=======================The choice like task======================
 
 
−
radio_pic_1.onchange = function() {f = 0;rebild();};//свободное тело
+
radio_pic_1.onchange = function() {f = 0;rebild();};//the free body
−
radio_pic_2.onchange = function() {f = 1;rebild();};//закрепленный край
+
radio_pic_2.onchange = function() {f = 1;rebild();};//the fixed edge
−
radio_pic_3.onchange = function() {f = 2;rebild();};//закрепелнные края
+
radio_pic_3.onchange = function() {f = 2;rebild();};//the fixed edges
 
 
−
// Реакция на изменение значения в чекбоксе
+
// Reaction to change of value in a checkbox
 
 
 
this.new_start = function()  
 
this.new_start = function()  
Строка 238: Строка 239:
 
var b1 = [];
 
var b1 = [];
 
var time = 1;
 
var time = 1;
−
b.fi_x = ugol*j; //угол с осью ОХ
+
b.fi_x = ugol*j; //corner with an axis ОХ
−
b.omega=0;//угловая скорость
+
b.omega=0;//angular velocity
−
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//смещение для рисования.  
+
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing.  
 
j=j*(-1);
 
j=j*(-1);
−
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // расчетные координаты шара
+
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
 
b.Fx=0;b.Fy=0;
 
b.Fx=0;b.Fy=0;
 
b.x_ = b.x;              b.y_  = b.y;  
 
b.x_ = b.x;              b.y_  = b.y;  
−
b.fx = 0;                b.fy  = 0;      // сила, действующая на шар
+
b.fx = 0;                b.fy  = 0;      // force operating on a sphere
−
b.vx = vx0;              b.vy  = vy0;      // начальная скорость
+
b.vx = vx0;              b.vy  = vy0;      // initial velocity
−
b1.fi_x = ugol*j; //угол с осью ОХ
+
b1.fi_x = ugol*j; //corner with an axis ОХ
 
b1.omega=0;
 
b1.omega=0;
 
b1.Fx=0;b1.Fy=0;
 
b1.Fx=0;b1.Fy=0;
−
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h /  (2.00-sm_y/100) ;    // расчетные координаты шара
+
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h /  (2.00-sm_y/100) ;    // force operating on a sphere
 
b1.x_ = b.x;              b1.y_  = b.y;  
 
b1.x_ = b.x;              b1.y_  = b.y;  
−
b1.fx = 0;                b1.fy  = 0;      // сила, действующая на шар
+
b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
−
b1.vx = vx0;              b1.vy  = vy0;      // начальная скорость
+
b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2+(i)] = b1;//[2*i+1]
 
balls[n/2+(i)] = b1;//[2*i+1]
Строка 271: Строка 272:
 
var time = 1;
 
var time = 1;
 
 
−
b.fi_x = ugol*j; //угол с осью ОХ
+
b.fi_x = ugol*j; //corner with an axis ОХ
−
b.omega=0;//угловая скорость
+
b.omega=0;//angular velocity
−
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//смещение для рисования.  
+
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing.  
 
j=j*(-1);
 
j=j*(-1);
−
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // расчетные координаты шара
+
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
 
b.Fx=0;b.Fy=0;
 
b.Fx=0;b.Fy=0;
 
b.x_ = b.x;              b.y_  = b.y;  
 
b.x_ = b.x;              b.y_  = b.y;  
−
b.fx = 0;                b.fy  = 0;      // сила, действующая на шар
+
b.fx = 0;                b.fy  = 0;      // force operating on a sphere
−
b.vx = vx0;              b.vy  = vy0;      // начальная скорость
+
b.vx = vx0;              b.vy  = vy0;      // initial velocity
−
b1.fi_x = ugol*j; //угол с осью ОХ
+
b1.fi_x = ugol*j; //corner with an axis OX
 
b1.omega=0;
 
b1.omega=0;
 
b1.Fx=0;b1.Fy=0;
 
b1.Fx=0;b1.Fy=0;
−
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h /  (2.00-sm_y/100) ;    // расчетные координаты шара
+
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h /  (2.00-sm_y/100) ;    // calculated coordinates of a sphere
 
b1.x_ = b.x;              b1.y_  = b.y;  
 
b1.x_ = b.x;              b1.y_  = b.y;  
−
b1.fx = 0;                b1.fy  = 0;      // сила, действующая на шар
+
b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
−
b1.vx = vx0;              b1.vy  = vy0;      // начальная скорость
+
b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2+(i)] = b1;//[2*i+1]
 
balls[n/2+(i)] = b1;//[2*i+1]
Строка 303: Строка 304:
 
var time = 1;
 
var time = 1;
 
 
−
b.fi_x = 10*j; //угол с осью ОХ
+
b.fi_x = 10*j; //corner with an axis OX
−
b.omega=0;//угловая скорость
+
b.omega=0;//angular velocity
−
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//смещение для рисования.  
+
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing.  
 
j=j*(-1);
 
j=j*(-1);
−
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.00;    // расчетные координаты шара
+
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.00;    // calculated coordinates of a sphere
−
 
 
b.Fx=0;b.Fy=0;
 
b.Fx=0;b.Fy=0;
 
b.x_ = b.x;              b.y_  = b.y;  
 
b.x_ = b.x;              b.y_  = b.y;  
−
b.fx = 0;                b.fy  = 0;      // сила, действующая на шар
+
b.fx = 0;                b.fy  = 0;      // force operating on a sphere
−
b.vx = vx0;              b.vy  = vy0;      // начальная скорость
+
b.vx = vx0;              b.vy  = vy0;      // initial velocity
−
b1.fi_x = 10*j; //угол с осью ОХ
+
b1.fi_x = 10*j; //corner with an axis OX
 
b1.omega=0;
 
b1.omega=0;
 
b1.Fx=0;b1.Fy=0;
 
b1.Fx=0;b1.Fy=0;
−
b1.x = (w / 2)+diag*(2*i+1)*1.0;          b1.y = h / 2 ;    // расчетные координаты шара
+
b1.x = (w / 2)+diag*(2*i+1)*1.0;          b1.y = h / 2 ;    // calculated coordinates of a sphere
 
b1.x_ = b.x;              b1.y_  = b.y;  
 
b1.x_ = b.x;              b1.y_  = b.y;  
−
b1.fx = 0;                b1.fy  = 0;      // сила, действующая на шар
+
b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
−
b1.vx = vx0;              b1.vy  = vy0;      // начальная скорость
+
b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2+(i)] = b1;//[2*i+1]
 
balls[n/2+(i)] = b1;//[2*i+1]
Строка 336: Строка 336:
 
var time = 1;
 
var time = 1;
 
 
−
b.fi_x = ugol*j; //угол с осью ОХ
+
b.fi_x = ugol*j; //corner with an axis OX
−
b.omega=0;//угловая скорость
+
b.omega=0;//angular velocity
−
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//смещение для рисования.  
+
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing.  
 
j=j*(-1);
 
j=j*(-1);
−
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // расчетные координаты шара
+
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
 
 
 
b.Fx=0;b.Fy=0;
 
b.Fx=0;b.Fy=0;
 
b.x_ = b.x;              b.y_  = b.y;  
 
b.x_ = b.x;              b.y_  = b.y;  
−
b.fx = 0;                b.fy  = 0;      // сила, действующая на шар
+
b.fx = 0;                b.fy  = 0;      // force operating on a sphere
−
b.vx = vx0;              b.vy  = vy0;      // начальная скорость
+
b.vx = vx0;              b.vy  = vy0;      // initial velocity
−
b1.fi_x = ugol*j; //угол с осью ОХ
+
b1.fi_x = ugol*j; //corner with an axis OX
 
b1.omega=0;
 
b1.omega=0;
 
b1.Fx=0;b1.Fy=0;
 
b1.Fx=0;b1.Fy=0;
−
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h /  (2.00-sm_y/100) ;    // расчетные координаты шара
+
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h /  (2.00-sm_y/100) ;    // calculated coordinates of a sphere
 
b1.x_ = b.x;              b1.y_  = b.y;  
 
b1.x_ = b.x;              b1.y_  = b.y;  
−
b1.fx = 0;                b1.fy  = 0;      // сила, действующая на шар
+
b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
−
b1.vx = vx0;              b1.vy  = vy0;      // начальная скорость
+
b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2+(i)] = b1;//[2*i+1]
 
balls[n/2+(i)] = b1;//[2*i+1]
Строка 373: Строка 373:
 
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);
 
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);
 
j=j*(-1);
 
j=j*(-1);
−
b1.fi_x = ugol*j; //угол с осью ОХ
+
b1.fi_x = ugol*j; //corner with an axis OX
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
break;
 
break;
 
case 1:
 
case 1:
−
if (i ==((n/2)-1))//закрепление края
+
if (i ==((n/2)-1))//fixing of edge
 
{
 
{
 
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
 
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
 
b.fi_x = 0;
 
b.fi_x = 0;
−
b1.fi_x = ugol*j; //угол с осью ОХ
+
b1.fi_x = ugol*j; //corner with an axis OX
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
}
 
}
Строка 387: Строка 387:
 
{
 
{
 
b.fi_x = ugol*j;
 
b.fi_x = ugol*j;
−
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // расчетные координаты шара
+
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
 
j=j*(-1);
 
j=j*(-1);
−
b1.fi_x = ugol*j; //угол с осью ОХ
+
b1.fi_x = ugol*j; //corner with an axis OX
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
}
 
}
 
break;
 
break;
 
case 2:
 
case 2:
−
if (i ==((n/2)-1))//закрепление краев
+
if (i ==((n/2)-1))//fixing of edges
 
{
 
{
 
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
 
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
Строка 404: Строка 404:
 
{
 
{
 
b.fi_x = ugol*j;
 
b.fi_x = ugol*j;
−
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // расчетные координаты шара
+
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
 
j=j*(-1);
 
j=j*(-1);
−
b1.fi_x = ugol*j; //угол с осью ОХ
+
b1.fi_x = ugol*j; //corner with an axis OX
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
}
 
}
 
break;
 
break;
 
}
 
}
−
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//смещение для рисования.  
+
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing.  
 
b.omega=0;
 
b.omega=0;
 
b.Fx=0;b.Fy=0;
 
b.Fx=0;b.Fy=0;
 
b.x_ = b.x;              b.y_  = b.y;  
 
b.x_ = b.x;              b.y_  = b.y;  
−
b.fx = 0;                b.fy  = 0;      // сила, действующая на шар
+
b.fx = 0;                b.fy  = 0;      // force operating on a sphere
−
b.vx = vx0;              b.vy  = vy0;      // начальная скорость
+
b.vx = vx0;              b.vy  = vy0;      // initial velocity
 
b1.omega=0;
 
b1.omega=0;
 
b1.Fx=0;b1.Fy=0;
 
b1.Fx=0;b1.Fy=0;
 
b1.x_ = b.x;              b1.y_  = b.y;  
 
b1.x_ = b.x;              b1.y_  = b.y;  
−
b1.fx = 0;                b1.fy  = 0;      // сила, действующая на шар
+
b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
−
b1.vx = vx0;              b1.vy  = vy0;      // начальная скорость
+
b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2+(i)] = b1;//[2*i+1]
 
balls[n/2+(i)] = b1;//[2*i+1]
Строка 444: Строка 444:
 
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);
 
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);
 
j=j*(-1);
 
j=j*(-1);
−
b1.fi_x = ugol*j; //угол с осью ОХ
+
b1.fi_x = ugol*j; //corner with an axis OX
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
break;
 
break;
 
case 1:
 
case 1:
−
if (i ==((n/2)-1))//закрепление края
+
if (i ==((n/2)-1))//fixing of edge
 
{
 
{
 
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
 
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
 
b.fi_x = 0;
 
b.fi_x = 0;
−
b1.fi_x = ugol*j; //угол с осью ОХ
+
b1.fi_x = ugol*j; //corner with an axis OX
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
}
 
}
Строка 458: Строка 458:
 
{
 
{
 
b.fi_x = ugol*j;
 
b.fi_x = ugol*j;
−
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // расчетные координаты шара
+
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
 
j=j*(-1);
 
j=j*(-1);
−
b1.fi_x = ugol*j; //угол с осью ОХ
+
b1.fi_x = ugol*j; //corner with an axis OX
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
}
 
}
 
break;
 
break;
 
case 2:
 
case 2:
−
if (i ==((n/2)-1))//закрепление краев
+
if (i ==((n/2)-1))//fixing of edges
 
{
 
{
 
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
 
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
Строка 475: Строка 475:
 
{
 
{
 
b.fi_x = ugol*j;
 
b.fi_x = ugol*j;
−
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // расчетные координаты шара
+
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
 
j=j*(-1);
 
j=j*(-1);
−
b1.fi_x = ugol*j; //угол с осью ОХ
+
b1.fi_x = ugol*j; //corner with an axis OX
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
}
 
}
 
break;
 
break;
 
}
 
}
−
b.omega=0;//угловая скорость
+
b.omega=0;//angular velocity
−
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//смещение для рисования.  
+
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing.  
 
b.Fx=0;b.Fy=0;
 
b.Fx=0;b.Fy=0;
 
b.x_ = b.x;              b.y_  = b.y;  
 
b.x_ = b.x;              b.y_  = b.y;  
−
b.fx = 0;                b.fy  = 0;      // сила, действующая на шар
+
b.fx = 0;                b.fy  = 0;      // force operating on a sphere
−
b.vx = vx0;              b.vy  = vy0;      // начальная скорость
+
b.vx = vx0;              b.vy  = vy0;      // initial velocity
 
b1.omega=0;
 
b1.omega=0;
 
b1.Fx=0;b1.Fy=0;
 
b1.Fx=0;b1.Fy=0;
 
b1.x_ = b.x;              b1.y_  = b.y;  
 
b1.x_ = b.x;              b1.y_  = b.y;  
−
b1.fx = 0;                b1.fy  = 0;      // сила, действующая на шар
+
b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
−
b1.vx = vx0;              b1.vy  = vy0;      // начальная скорость
+
b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2+(i)] = b1;//[2*i+1]
 
balls[n/2+(i)] = b1;//[2*i+1]
Строка 514: Строка 514:
 
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);
 
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);
 
j=j*(-1);
 
j=j*(-1);
−
b1.fi_x = ugol*j; //угол с осью ОХ
+
b1.fi_x = ugol*j; //corner with an axis OX
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
break;
 
break;
 
case 1:
 
case 1:
−
if (i ==((n/2)-1))//закрепление края
+
if (i ==((n/2)-1))//fixing of edge
 
{
 
{
 
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
 
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
 
b.fi_x = 0;
 
b.fi_x = 0;
−
b1.fi_x = ugol*j; //угол с осью ОХ
+
b1.fi_x = ugol*j; //corner with an axis OX
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
}
 
}
Строка 528: Строка 528:
 
{
 
{
 
b.fi_x = ugol*j;
 
b.fi_x = ugol*j;
−
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // расчетные координаты шара
+
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
 
j=j*(-1);
 
j=j*(-1);
−
b1.fi_x = ugol*j; //угол с осью ОХ
+
b1.fi_x = ugol*j; //corner with an axis OX
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
}
 
}
 
break;
 
break;
 
case 2:
 
case 2:
−
if (i ==((n/2)-1))//закрепление краев
+
if (i ==((n/2)-1))//fixing of edges
 
{
 
{
 
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
 
b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
Строка 545: Строка 545:
 
{
 
{
 
b.fi_x = ugol*j;
 
b.fi_x = ugol*j;
−
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // расчетные координаты шара
+
b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
 
j=j*(-1);
 
j=j*(-1);
−
b1.fi_x = ugol*j; //угол с осью ОХ
+
b1.fi_x = ugol*j; //corner with an axis OX
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
 
}
 
}
 
break;
 
break;
 
}
 
}
−
b.omega=0;//угловая скорость
+
b.omega=0;//angular velocity
−
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//смещение для рисования.  
+
var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing.  
 
b.Fx=0;b.Fy=0;
 
b.Fx=0;b.Fy=0;
 
b.x_ = b.x;              b.y_  = b.y;  
 
b.x_ = b.x;              b.y_  = b.y;  
−
b.fx = 0;                b.fy  = 0;      // сила, действующая на шар
+
b.fx = 0;                b.fy  = 0;      // force operating on a sphere
−
b.vx = vx0;              b.vy  = vy0;      // начальная скорость
+
b.vx = vx0;              b.vy  = vy0;      // initial velocity
 
b1.omega=0;
 
b1.omega=0;
 
b1.Fx=0;b1.Fy=0;
 
b1.Fx=0;b1.Fy=0;
 
b1.x_ = b.x;              b1.y_  = b.y;  
 
b1.x_ = b.x;              b1.y_  = b.y;  
−
b1.fx = 0;                b1.fy  = 0;      // сила, действующая на шар
+
b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
−
b1.vx = vx0;              b1.vy  = vy0;      // начальная скорость
+
b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2-(i+1)]=b;//[2*i]
 
balls[n/2+(i)] = b1;//[2*i+1]
 
balls[n/2+(i)] = b1;//[2*i+1]
Строка 569: Строка 569:
 
         context.clearRect(0, 0, w * scale, h * scale);       
 
         context.clearRect(0, 0, w * scale, h * scale);       
 
};
 
};
−
// Функция, делающая spf шагов интегрирования
+
// The function doing spf of integration steps
 
function physics()  
 
function physics()  
−
{                    // то, что происходит каждый шаг времени
+
{                    // the fact that there is each step of time
−
    for (var s = 1; s <= spf; s++) //шаги интегрирования
+
    for (var s = 1; s <= spf; s++) //integration step
 
{   
 
{   
 
 
Строка 604: Строка 604:
 
var beta_y=0.01//0.1;
 
var beta_y=0.01//0.1;
 
//console.log(c_b);
 
//console.log(c_b);
−
if (f==0)//совбодное тело
+
if (f==0)//the free body
 
{
 
{
 
x_v1=balls[i].vx;
 
x_v1=balls[i].vx;
Строка 628: Строка 628:
 
asd=balls[0].fx+balls[1].fx;
 
asd=balls[0].fx+balls[1].fx;
 
}
 
}
−
else//закрепелнный край
+
else//the fixed edge
 
{
 
{
−
if (f==1)////закрепелнный край
+
if (f==1)////the fixed edge
 
{
 
{
 
balls[i] = b;
 
balls[i] = b;
Строка 656: Строка 656:
 
}
 
}
 
}
 
}
−
else //оба края закрепелены
+
else //both edges are fixed
 
{
 
{
 
 
Строка 691: Строка 691:
 
}
 
}
 
}
 
}
−
// определение функции, вычисляющей силу
+
// definition of the function calculating force
  
−
     // определение функции, рисующией частицу, стенки и пр
+
     // definition of function, risuyushchiy particle, walls and other
−
     context.fillStyle = "#3070d0"; // цвет
+
     context.fillStyle = "#3070d0"; // colour
−
//===================================Взаимодествие мышью========================
+
//===================================Interaction by a mouse========================
−
// функция запускается при нажатии клавиши мыши
+
// function is started when pressing a key of a mouse
 
     canvasBalls.onmousedown = function(e) {
 
     canvasBalls.onmousedown = function(e) {
−
         var m = mouseCoords(e);                    // получаем координаты курсора мыши
+
         var m = mouseCoords(e);                    // we receive cursor coordinates of a mouse
 
         switch (f)  
 
         switch (f)  
 
{
 
{
 
case(0):
 
case(0):
−
var x = balls[n-1].x - m.x/scale;                          // расстояние от центра шара до курсора по оси x
+
var x = balls[n-1].x - m.x/scale;                          // distance from the center of a sphere to the cursor on an axis x
−
var y = balls[n-1].y - m.y/scale;                          // расстояние от центра шара до курсора по оси y
+
var y = balls[n-1].y - m.y/scale;                          // distance from the center of a sphere to the cursor on an axis y
−
var rLen2 = x * x + y * y;                  // квадрат расстояния между курсором и центром шара
+
var rLen2 = x * x + y * y;                  // distance square between the cursor and the center of a sphere
−
if (rLen2 <= diag*diag) {                      // если курсор нажал на шар
+
if (rLen2 <= diag*diag) {                      // if the cursor pressed a sphere
−
xShift = balls[n-1].x - m.x/scale;                      // сдвиг курсора относительно центра шара по x
+
xShift = balls[n-1].x - m.x/scale;                      // shift of the cursor concerning the center of a sphere on x
−
yShift = balls[n-1].y - m.y/scale;                      // сдвиг курсора относительно центра шара по y
+
yShift = balls[n-1].y - m.y/scale;                      // shift of the cursor concerning the center of a sphere for y
−
canvasBalls.onmousemove = mouseMove; // пока клавиша нажата - работает функция перемещения
+
canvasBalls.onmousemove = mouseMove; // until the key is pressed - movement function works
 
}
 
}
 
break;
 
break;
 
case(1):
 
case(1):
−
var x = balls[n-1].x - m.x/scale;                          // расстояние от центра шара до курсора по оси x
+
var x = balls[n-1].x - m.x/scale;                          // distance from the center of a sphere to the cursor on an axis x
−
var y = balls[n-1].y - m.y/scale;                          // расстояние от центра шара до курсора по оси y
+
var y = balls[n-1].y - m.y/scale;                          // distance from the center of a sphere to the cursor on an axis y
−
var rLen2 = x * x + y * y;                  // квадрат расстояния между курсором и центром шара
+
var rLen2 = x * x + y * y;                  // distance square between the cursor and the center of a sphere
−
if (rLen2 <= diag*diag) {                      // если курсор нажал на шар
+
if (rLen2 <= diag*diag) {                      // if the cursor pressed a sphere
−
xShift = balls[n-1].x - m.x/scale;                      // сдвиг курсора относительно центра шара по x
+
xShift = balls[n-1].x - m.x/scale;                      // shift of the cursor concerning the center of a sphere on x
−
yShift = balls[n-1].y - m.y/scale;                      // сдвиг курсора относительно центра шара по y
+
yShift = balls[n-1].y - m.y/scale;                      // shift of the cursor concerning the center of a sphere for y
−
canvasBalls.onmousemove = mouseMove; // пока клавиша нажата - работает функция перемещения
+
canvasBalls.onmousemove = mouseMove; // until the key is pressed - movement function works
 
}
 
}
 
break;
 
break;
 
case (2):
 
case (2):
 
case(0):
 
case(0):
−
var x = balls[n/2].x - m.x/scale;                          // расстояние от центра шара до курсора по оси x
+
var x = balls[n/2].x - m.x/scale;                          // distance from the center of a sphere to the cursor on an axis x
−
var y = balls[n/2].y - m.y/scale;                          // расстояние от центра шара до курсора по оси y
+
var y = balls[n/2].y - m.y/scale;                          // distance from the center of a sphere to the cursor on an axis y
−
var rLen2 = x * x + y * y;                  // квадрат расстояния между курсором и центром шара
+
var rLen2 = x * x + y * y;                  // distance square between the cursor and the center of a sphere
−
if (rLen2 <= diag*diag) {                      // если курсор нажал на шар
+
if (rLen2 <= diag*diag) {                      // if the cursor pressed a sphere
−
xShift = balls[n/2].x - m.x/scale;                      // сдвиг курсора относительно центра шара по x
+
xShift = balls[n/2].x - m.x/scale;                      // shift of the cursor concerning the center of a sphere on x
−
yShift = balls[n/2].y - m.y/scale;                      // сдвиг курсора относительно центра шара по y
+
yShift = balls[n/2].y - m.y/scale;                      // shift of the cursor concerning the center of a sphere for y
−
canvasBalls.onmousemove = mouseMove; // пока клавиша нажата - работает функция перемещения
+
canvasBalls.onmousemove = mouseMove; // until the key is pressed - movement function works
 
}
 
}
 
break;
 
break;
Строка 735: Строка 735:
 
     };
 
     };
 
   
 
   
−
     // функция запускается при отпускании клавиши мыши
+
     // function is started at a key release of a mouse
 
     document.onmouseup = function() {
 
     document.onmouseup = function() {
−
         canvasBalls.onmousemove = null;        // когда клавиша отпущена - функции перемещения нету
+
         canvasBalls.onmousemove = null;        // when the key is released - there is no function of movement
 
     };
 
     };
 
   
 
   
−
     // функция запускается при перемещении мыши (много раз, в каждый момент перемещения)
+
     // function is started when moving a mouse (many times, at every moment of movement)
−
     // в нашем случае работает только с зажатой клавишей мыши
+
     // in our case works only with a viced key of a mouse
 
     function mouseMove(e) {
 
     function mouseMove(e) {
 
switch (f)
 
switch (f)
 
{
 
{
 
case(0):
 
case(0):
−
var m = mouseCoords(e);                    // получаем координаты курсора мыши
+
var m = mouseCoords(e);                    // we receive cursor coordinates of a mouse
 
balls[n-1].x = m.x/scale + xShift;
 
balls[n-1].x = m.x/scale + xShift;
 
balls[n-1].y = m.y/scale+ yShift;
 
balls[n-1].y = m.y/scale+ yShift;
Строка 760: Строка 760:
 
console.log(m.x/scale);
 
console.log(m.x/scale);
 
//console.log(r_nach);
 
//console.log(r_nach);
−
if (Math.abs(r_m)<(3*diag)) // получаем координаты курсора мыши
+
if (Math.abs(r_m)<(3*diag)) // we receive cursor coordinates of a mouse
 
{pr_x = m.x/scale + xShift*0.01 -balls[n-1].x;
 
{pr_x = m.x/scale + xShift*0.01 -balls[n-1].x;
 
pr_y = m.y/scale+yShift-balls[n-1].y;
 
pr_y = m.y/scale+yShift-balls[n-1].y;
Строка 769: Строка 769:
 
break;
 
break;
 
case(2):
 
case(2):
−
var m = mouseCoords(e);                    // получаем координаты курсора мыши
+
var m = mouseCoords(e);                    // we receive cursor coordinates of a mouse balls[n/2].x = m.x/scale + xShift;
−
balls[n/2].x = m.x/scale + xShift;
 
 
balls[n/2].y = m.y/scale+ yShift;
 
balls[n/2].y = m.y/scale+ yShift;
 
draw();
 
draw();
Строка 777: Строка 776:
 
     }
 
     }
 
   
 
   
−
     // функция возвращает координаты курсора мыши
+
     // function returns cursor coordinates of a mouse
 
     function mouseCoords(e) {
 
     function mouseCoords(e) {
 
         var m = [];
 
         var m = [];
Строка 795: Строка 794:
 
     function draw()  
 
     function draw()  
 
{       
 
{       
−
         context.clearRect(0, 0, w * scale, h * scale); // очистить экран
+
         context.clearRect(0, 0, w * scale, h * scale); // to clear the screen
 
         for (var i =0;i<n;i++)
 
         for (var i =0;i<n;i++)
 
{
 
{
 
    b = balls[i];
 
    b = balls[i];
 
context.beginPath();
 
context.beginPath();
−
context.translate(b.x*scale,b.y * scale);//перенос в центр
+
context.translate(b.x*scale,b.y * scale);//transfer in the center
 
context.rotate(inRad(b.fi_x-45));
 
context.rotate(inRad(b.fi_x-45));
 
context.fillRect(-rectW/2, -rectH/2, rectW, rectH);
 
context.fillRect(-rectW/2, -rectH/2, rectW, rectH);
 
context.rotate(-inRad(b.fi_x-45));
 
context.rotate(-inRad(b.fi_x-45));
−
context.translate(-b.x * scale, -b.y * scale);//перенос обратно
+
context.translate(-b.x * scale, -b.y * scale);//transfer back
 
context.closePath();
 
context.closePath();
 
context.stroke();  
 
context.stroke();  
Строка 812: Строка 811:
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
Файл '''"v-model.html"'''
+
File '''"v-model.html"'''
 
<syntaxhighlight lang="html5" line start="1" enclose="div">
 
<syntaxhighlight lang="html5" line start="1" enclose="div">
 
  <!DOCTYPE html>
 
  <!DOCTYPE html>
Строка 821: Строка 820:
 
  </head>
 
  </head>
 
  <body>
 
  <body>
−
  <!-- Добавление области для рисования частицы -->
+
  <!-- Addition of area for drawing of a particle -->
 
     <canvas id="canvasBalls" width="800" height="400" style="border:1px solid #000000;"></canvas>
 
     <canvas id="canvasBalls" width="800" height="400" style="border:1px solid #000000;"></canvas>
 
 
Строка 831: Строка 830:
 
             <!-- document.getElementById('Slider_02').value = this.value; -->
 
             <!-- document.getElementById('Slider_02').value = this.value; -->
 
         ">
 
         ">
−
<!-- Добавление слайдера -->
+
<!-- Addition of a slider -->
 
         <!-- <input type="range" id="Slider_02" style="width: 100px;" oninput="app.set_02(this.value); document.getElementById('Text_02').value = this.value;"> -->
 
         <!-- <input type="range" id="Slider_02" style="width: 100px;" oninput="app.set_02(this.value); document.getElementById('Text_02').value = this.value;"> -->
 
         </I></font>
 
         </I></font>
Строка 840: Строка 839:
 
             <!-- document.getElementById('Slider_02').value = this.value; -->
 
             <!-- document.getElementById('Slider_02').value = this.value; -->
 
         ">
 
         ">
−
<!-- Добавление слайдера -->
+
<!-- Addition of a slider -->
 
         <!-- <input type="range" id="Slider_02" style="width: 100px;" oninput="app.set_02(this.value); document.getElementById('Text_02').value = this.value;"> -->
 
         <!-- <input type="range" id="Slider_02" style="width: 100px;" oninput="app.set_02(this.value); document.getElementById('Text_02').value = this.value;"> -->
 
         </I></font>
 
         </I></font>
Строка 849: Строка 848:
 
             <!-- document.getElementById('Slider_02').value = this.value; -->
 
             <!-- document.getElementById('Slider_02').value = this.value; -->
 
         ">
 
         ">
−
<!-- Добавление слайдера -->
+
<!-- Addition of a slider -->
 
         <!-- <input type="range" id="Slider_02" style="width: 100px;" oninput="app.set_02(this.value); document.getElementById('Text_02').value = this.value;"> -->
 
         <!-- <input type="range" id="Slider_02" style="width: 100px;" oninput="app.set_02(this.value); document.getElementById('Text_02').value = this.value;"> -->
 
         </I></font>
 
         </I></font>
Строка 858: Строка 857:
 
             <!-- document.getElementById('Slider_02').value = this.value; -->
 
             <!-- document.getElementById('Slider_02').value = this.value; -->
 
         ">
 
         ">
−
<!-- Добавление слайдера -->
+
<!-- Addition of a slider -->
 
         <!-- <input type="range" id="Slider_02" style="width: 100px;" oninput="app.set_02(this.value); document.getElementById('Text_02').value = this.value;"> -->
 
         <!-- <input type="range" id="Slider_02" style="width: 100px;" oninput="app.set_02(this.value); document.getElementById('Text_02').value = this.value;"> -->
 
         </I></font>
 
         </I></font>

Текущая версия на 19:06, 18 января 2017

The virtual laboratory > Particles chain with V-model interaction

The short description of V - model[править]

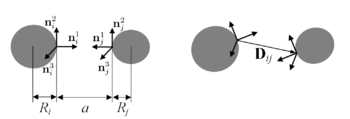
V-model is used for the description of loose solid bodies, for example rocks, ceramics, concrete, nanocomposites and agglomerates.

The model is described by the following formulas:

Interaction of two particles

Interaction force:

[math]\mathbf{F_{ij}} = B_1 ( D_{ij} - a) \mathbf{d_{ij}} + \frac{B_2}{2D_{ij}}(\mathbf{n_{j1}} - \mathbf{n_{i1}})\cdot(\mathbf{E}-\mathbf{d_{ij}}\mathbf{d_{ij}}) [/math]

Moments:

[math]\mathbf{M_{ij}} = R_i \mathbf{n_{i1}} \times \mathbf{F_{ij}} - \frac{B_2}{2}\mathbf{d_{ij}}\times \mathbf{n_{i1}}+\mathbf{M_{tb}} [/math]

[math]\mathbf{M_{ji}} = R_i \mathbf{n_{j1}} \times \mathbf{F_{ji}} + \frac{B_2}{2}\mathbf{d_{ij}}\times \mathbf{n_{j1}}-\mathbf{M_{tb}} [/math]

[math]\mathbf{M_{tb}} = B_3 \mathbf{n_{j1}} \times \mathbf{n_{i1}} - \frac{B_4}{2}(\mathbf{n_{j2}}\times \mathbf{n_{i2}}+\mathbf{n_{j3}}\times \mathbf{n_{i3}}) [/math]

Where [math]B_1[/math], [math]B_2[/math], [math]B_3[/math] and [math]B_4[/math] - various coefficients which are characteristics of system.


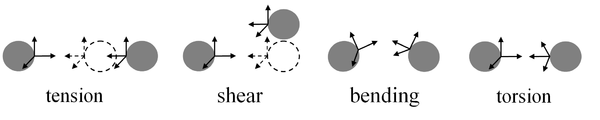
Description of realization of a chain[править]

Types of deformations

In the program three various boundary conditions which can are realized chosen as the user:

  • The free chain
  • Chain with clenched left edge
  • Chain with clenched edges

Also the user in the first two cases can move an extreme right particle, and in the third case can move the central right particle.

An opportunity to set starting conditions for all chains is provided:

  • To set an amount of twist of particles from each other.
  • To set the relative displacement of particles along OX axis
  • To set the relative displacement of particles along OY axis

Also there is an opportunity to set stiffness factors of system on various movements. Which are bound to coefficients from the formulas stated above for V - model.

  • Rigidity on stretching compression: [math]c_a = B_1 [/math]
  • Rigidity on shift: [math]c_d = \frac{B_2}{a^2} [/math]
  • Rigidity on a bend: [math]c_b = \frac{B_2}{4} + B_3 +\frac{B_4}{2} [/math]
  • Rigidity on torsion: [math]c_t = B_4 [/math]

Realization of a chain[править]

The program given below realizes a chain of particles, interaction between which is V - model.

Download V-model.

The text of the program in the JavaScript (developer Lapin Ruslan):

File "V-model.js" 

  1 function MainParticle(canvas) {
  2     // Presets
  3     var context    = canvas.getContext("2d");  // on context drawing takes place
  4 	
  5    //  Specifying constants	
  6     const Pi = 3.1415926;                   // "Pi"
  7     const m0 = 1;                           // weight scale
  8     const T0 = 1;                           // time scale (the period of oscillation of the original system )
  9     const a0 = 1;                           // distance scale ( ball diameter)
 10     const g0 = a0 / T0 / T0;                // accelerating the scale (acceleration , in which for T0 be completed distance a0)
 11     const k0 = 2 * Pi / T0;                 // frequency scale
 12     //const C0 = m0 * k0 * k0;                // hardness scale
 13     const C0 = 1;
 14     const B0 = 2 * m0 * k0;                 // viscosity scale
 15 
 16     // *** Setting physical parameters ***
 17 
 18     const Ny = 5;                           // the number of balls is placed vertically in a window ( sets the size of the ball relative to the window size )
 19     const Nx = 5;
 20 	const m = 1 * m0;                       // weight
 21     const Cwall = 10 * C0;                  // wall stiffness
 22     //const B = 0.01 * B0;  // viscosity of the environment
 23     const B = 0;
 24     const B1 = 0.03 * B0;                   // viscosity on the walls
 25     //const B1 = 0;
 26     //var mg = 0.25 * m * g0;               // gravity
 27     const r = 0.5 * a0;                     // the radius of the particles in the calculated coordinates
 28 	var stiff = 1 * C0;                     // "Rigidity" of a spring
 29 
 30 	var vx0 = 0 * a0/T0;
 31 	var vy0 = 0 * a0/T0;
 32     //Text_vx0.value  = vx0;
 33 	
 34     // *** System settings ***
 35 	var c = 1;// rigidity
 36 	var n = 10;// the amount of particles
 37 	var c_a = 100//1;//longitudinal
 38 	var c_d = 100//c_a*1;//shear
 39 	var c_b = 0.1//c_a;//bending
 40 	var c_t = 1;//torsional
 41 	var J = 1;
 42 	var m_0 = 1.5;
 43 	var f = 0	;//option or free body or fixed edge
 44 	var ugol = 0;
 45 	var sm_x = 0;
 46 	var sm_y = 0;
 47 	
 48 	
 49     // *** Setting the parameters of computing ***
 50 
 51     const fps = 50;                         // frames per second - the number of frames per second ( kachectvo display )50
 52     const spf = 10;//5;                        // steps per frame   - the number of integration steps between frames ( calculation speed)
 53     const dt  = 1 * T0 / fps;           // the integration step 
 54 	
 55 	// Setting constants for drawing
 56 	const scale    =100* canvas.height / Ny / a0;  // a scaling factor for the transition from design to screen coordinates
 57 	
 58     var w = canvas.width / scale;           // width of the window in the calculated coordinates
 59     var h = canvas.height / scale;          // window height in calculated coordinates
 60 	var k1v; var k2v; var k3v; var k4v; var k1x;  var k2x; var k3x; var k4x; 
 61 	var T1;var T2; var T1_; var T2_;
 62 	var rectH = 50;
 63 	var rectW = 50;
 64 	var diag = (rectH/scale)*Math.cos(45*Math.PI/180);
 65 	var koeff = 1;
 66 	var B_1 =c_a;
 67 	var B_2 = c_d*diag*diag;
 68 	var B_4 = c_t;
 69 	var B_3 = c_b - B_2/4 - B_4/2;
 70 	
 71     // -------------------------------         Implementation of the program              ------------------------------------------
 72 	// Addition of a sphere
 73 	balls=[]//the massif containing particles
 74 	j=1;
 75 	for (i = 0;i<n/2;i++)
 76 	{
 77 		var b = [];
 78 		var b1 = [];
 79 		var time = 1;
 80 		b.fi_x = 0*j; //corner with an axis OX
 81 		b.omega=0;// angular velocity
 82 		var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing. 
 83 		j=j*(-1);
 84 		b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;    // calculated coordinates of a sphere
 85 		b.Fx=0;b.Fy=0;
 86 		b.x_ = b.x;              b.y_  = b.y; 
 87 		b.fx = 0;                b.fy  = 0;      // force operating on a spher
 88 		b.vx = vx0;              b.vy  = vy0;      // initial velocity
 89 		b1.fi_x = 0*j; //corner with an axis OX
 90 		b1.omega=0;	
 91 		b1.Fx=0;b1.Fy=0;		
 92 		b1.x = (w / 2)+diag*(2*i+1)*1.0;          b1.y = h / 2 ;    // calculated coordinates of a sphere
 93 		b1.x_ = b.x;              b1.y_  = b.y; 
 94 		b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
 95 		b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
 96 		balls[n/2-(i+1)]=b;//[2*i]
 97 		balls[n/2+(i)] = b1;//[2*i+1]
 98 		
 99 	}
100 	// Basis cycle of the program
101 	setInterval(control, 1500 / fps);  // function control is caused with the period determined by the second parameter
102 	
103 // ---------------------------------------------------------------------------------------------------------------------
104 // ---------------------------------           Definition of all functions              -----------------------------------
105 // ---------------------------------------------------------------------------------------------------------------------
106 	
107 	// the trial function caused in the program
108 	function control() 
109 	{
110         physics(); // we do spf of steps an integration
111         draw();    // we draw a particle 
112 	}
113 	//=======================new task of a reference state
114 	function rebild()//new task of a reference state
115 	{
116 		time = 1;
117 		balls=[]
118 		j=1;
119 		ugol = 0;
120 		sm_x = 0;
121 		sm_y = 0;
122 		for (i = 0;i<n/2;i++)
123 		{
124 			var b = [];
125 			var b1 = [];
126 			var time = 1;
127 			b.fi_x = 0*j; //corner with an axis ОХ
128 			b.omega=0;//angular velocity
129 			var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing. 
130 			j=j*(-1);
131 			b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;    // calculated coordinates of a sphere
132 			b.Fx=0;b.Fy=0;
133 			b.x_ = b.x;              b.y_  = b.y; 
134 			b.fx = 0;                b.fy  = 0;      // force operating on a sphere
135 			b.vx = vx0;              b.vy  = vy0;      // initial velocity
136 			b1.fi_x = 0*j; //corner with an axis ОХ
137 			b1.omega=0;	
138 			b1.Fx=0;b1.Fy=0;		
139 			b1.x = (w / 2)+diag*(2*i+1)*1.0;          b1.y = h / 2 ;    // calculated coordinates of a sphere
140 			b1.x_ = b.x;              b1.y_  = b.y; 
141 			b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
142 			b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
143 			balls[n/2-(i+1)]=b;//[2*i]
144 			balls[n/2+(i)] = b1;//[2*i+1]
145 			
146 		}
147 		context.clearRect(0, 0, w * scale, h * scale); 
148 	}
149 	//=======================The choice like task======================
150 	
151 	radio_pic_1.onchange = function() {f = 0;rebild();};//the free body
152 	radio_pic_2.onchange = function() {f = 1;rebild();};//the fixed edge
153 	radio_pic_3.onchange = function() {f = 2;rebild();};//the fixed edges
154 	
155 	// Reaction to change of value in a checkbox
156 	
157 	this.new_start = function() 
158 	{
159 		rebild();
160 	}
161 	this.set_c_a = function(input) 
162 	{
163 		c_a = Number(input);   
164 		B_1 =c_a;
165 		time = 1;
166 		for (i = 0;i<n/2;i++)
167 		{
168 			var b = [];
169 			var b1 = [];
170 			var time = 1;
171 			b.fi_x = ugol*j; //corner with an axis ОХ
172 			b.omega=0;//angular velocity 
173 			var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing. 
174 			j=j*(-1);
175 			b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
176 			b.Fx=0;b.Fy=0;
177 			b.x_ = b.x;              b.y_  = b.y; 
178 			b.fx = 0;                b.fy  = 0;      // force operating on a sphere
179 			b.vx = vx0;              b.vy  = vy0;      // initial velocity
180 			b1.fi_x = ugol*j; //corner with an axis ОХ
181 			b1.omega=0;	
182 			b1.Fx=0;b1.Fy=0;		
183 			b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h /  (2.00-sm_y/100) ;    // force operating on a sphere
184 			b1.x_ = b.x;              b1.y_  = b.y; 
185 			b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
186 			b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
187 			balls[n/2-(i+1)]=b;//[2*i]
188 			balls[n/2+(i)] = b1;//[2*i+1]
189 			
190 		}
191         context.clearRect(0, 0, w * scale, h * scale);          
192 	}
193 	this.set_c_b = function(input) 
194 	{
195 		c_b = Number(input);   
196 		B_3 = c_b - B_2/4 - B_4/2;
197 		time = 1;
198 		for (i = 0;i<n/2;i++)
199 		{
200 			var b = [];
201 			var b1 = [];
202 			var time = 1;
203 			
204 			b.fi_x = ugol*j; //corner with an axis ОХ
205 			b.omega=0;//angular velocity
206 			var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing. 
207 			j=j*(-1);
208 			b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
209 			b.Fx=0;b.Fy=0;
210 			b.x_ = b.x;              b.y_  = b.y; 
211 			b.fx = 0;                b.fy  = 0;      // force operating on a sphere
212 			b.vx = vx0;              b.vy  = vy0;      // initial velocity
213 			b1.fi_x = ugol*j; //corner with an axis OX
214 			b1.omega=0;	
215 			b1.Fx=0;b1.Fy=0;		
216 			b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h /  (2.00-sm_y/100) ;    // calculated coordinates of a sphere
217 			b1.x_ = b.x;              b1.y_  = b.y; 
218 			b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
219 			b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
220 			balls[n/2-(i+1)]=b;//[2*i]
221 			balls[n/2+(i)] = b1;//[2*i+1]
222 			
223 		}
224     }
225 	this.set_c_d = function(input) 
226 	{
227 		c_d = Number(input);   
228 		B_2 = c_d*diag*diag;
229 		time = 1;
230 		for (i = 0;i<n/2;i++)
231 		{
232 			var b = [];
233 			var b1 = [];
234 			var time = 1;
235 			
236 			b.fi_x = 10*j; //corner with an axis OX
237 			b.omega=0;//angular velocity
238 			var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing. 
239 			j=j*(-1);
240 			b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.00;    // calculated coordinates of a sphere
241 			b.Fx=0;b.Fy=0;
242 			b.x_ = b.x;              b.y_  = b.y; 
243 			b.fx = 0;                b.fy  = 0;      // force operating on a sphere
244 			b.vx = vx0;              b.vy  = vy0;      // initial velocity
245 			b1.fi_x = 10*j; //corner with an axis OX
246 			b1.omega=0;	
247 			b1.Fx=0;b1.Fy=0;		
248 			b1.x = (w / 2)+diag*(2*i+1)*1.0;          b1.y = h / 2 ;    // calculated coordinates of a sphere
249 			b1.x_ = b.x;              b1.y_  = b.y; 
250 			b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
251 			b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
252 			balls[n/2-(i+1)]=b;//[2*i]
253 			balls[n/2+(i)] = b1;//[2*i+1]
254 		}
255         context.clearRect(0, 0, w * scale, h * scale);         
256 	}
257 	this.set_c_t = function(input) 
258 	{
259 		c_t = Number(input);   
260 		B_4 = c_t;
261 		time = 1;
262 		for (i = 0;i<n/2;i++)
263 		{
264 			var b = [];
265 			var b1 = [];
266 			var time = 1;
267 			
268 			b.fi_x = ugol*j; //corner with an axis OX
269 			b.omega=0;//angular velocity
270 			var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing. 
271 			j=j*(-1);
272 			b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
273 			
274 			b.Fx=0;b.Fy=0;
275 			b.x_ = b.x;              b.y_  = b.y; 
276 			b.fx = 0;                b.fy  = 0;      // force operating on a sphere
277 			b.vx = vx0;              b.vy  = vy0;      // initial velocity
278 			b1.fi_x = ugol*j; //corner with an axis OX
279 			b1.omega=0;	
280 			b1.Fx=0;b1.Fy=0;		
281 			b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h /  (2.00-sm_y/100) ;    // calculated coordinates of a sphere
282 			b1.x_ = b.x;              b1.y_  = b.y; 
283 			b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
284 			b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
285 			balls[n/2-(i+1)]=b;//[2*i]
286 			balls[n/2+(i)] = b1;//[2*i+1]
287 		}
288         context.clearRect(0, 0, w * scale, h * scale);      
289 	}
290 	
291 	slider_input.oninput = function() {
292         ugol = slider_input.value;
293 		time = 1;
294 		for (i = 0;i<n/2;i++)
295 		{
296 			var b = [];
297 			var b1 = [];
298 			var time = 1;
299 			switch (f)
300 			{
301 				case 0:
302 					b.fi_x = ugol*j;
303 					b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);
304 					j=j*(-1);
305 					b1.fi_x = ugol*j; //corner with an axis OX
306 					b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
307 					break;
308 				case 1:
309 					if (i ==((n/2)-1))//fixing of edge
310 					{
311 						b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
312 						b.fi_x = 0;		
313 						b1.fi_x = ugol*j; //corner with an axis OX
314 						b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
315 					}
316 					else
317 					{
318 						b.fi_x = ugol*j;
319 						b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
320 						j=j*(-1);
321 						b1.fi_x = ugol*j; //corner with an axis OX
322 						b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
323 					}
324 					break;
325 				case 2:
326 					if (i ==((n/2)-1))//fixing of edges
327 					{
328 						b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
329 						b.fi_x = 0;	
330 						b1.x = (w / 2)+diag*(2*i+1)*1.0;          b1.y = h / 2.0;
331 						b1.fi_x = 0;
332 					}
333 					else
334 					{
335 						b.fi_x = ugol*j;
336 						b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
337 						j=j*(-1);
338 						b1.fi_x = ugol*j; //corner with an axis OX
339 						b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
340 					}
341 					break;
342 			}
343 			var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing. 
344 			b.omega=0;
345 			b.Fx=0;b.Fy=0;
346 			b.x_ = b.x;              b.y_  = b.y; 
347 			b.fx = 0;                b.fy  = 0;      // force operating on a sphere
348 			b.vx = vx0;              b.vy  = vy0;      // initial velocity
349 			b1.omega=0;	
350 			b1.Fx=0;b1.Fy=0;		
351 			b1.x_ = b.x;              b1.y_  = b.y; 
352 			b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
353 			b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
354 			balls[n/2-(i+1)]=b;//[2*i]
355 			balls[n/2+(i)] = b1;//[2*i+1]
356 			
357 		}
358 		context.clearRect(0, 0, w * scale, h * scale);   
359 	};
360 	
361 	slider_input_ox.oninput = function() {
362         sm_x = slider_input_ox.value;
363 		time = 1;
364 		j=1;
365 		for (i = 0;i<n/2;i++)
366 		{
367 			var b = [];
368 			var b1 = [];
369 			var time = 1;
370 			switch (f)
371 			{
372 				case 0:
373 					b.fi_x = ugol*j;
374 					b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);
375 					j=j*(-1);
376 					b1.fi_x = ugol*j; //corner with an axis OX
377 					b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
378 					break;
379 				case 1:
380 					if (i ==((n/2)-1))//fixing of edge
381 					{
382 						b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
383 						b.fi_x = 0;	
384 						b1.fi_x = ugol*j; //corner with an axis OX
385 						b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;						
386 					}
387 					else
388 					{
389 						b.fi_x = ugol*j;
390 						b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
391 						j=j*(-1);
392 						b1.fi_x = ugol*j; //corner with an axis OX
393 						b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
394 					}
395 					break;
396 				case 2:
397 					if (i ==((n/2)-1))//fixing of edges
398 					{
399 						b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
400 						b.fi_x = 0;	
401 						b1.x = (w / 2)+diag*(2*i+1)*1.0;          b1.y = h / 2.0;
402 						b1.fi_x = 0;
403 					}
404 					else
405 					{
406 						b.fi_x = ugol*j;
407 						b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
408 						j=j*(-1);
409 						b1.fi_x = ugol*j; //corner with an axis OX
410 						b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
411 					}
412 					break;
413 			}
414 			b.omega=0;//angular velocity
415 			var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing. 
416 			b.Fx=0;b.Fy=0;
417 			b.x_ = b.x;              b.y_  = b.y; 
418 			b.fx = 0;                b.fy  = 0;      // force operating on a sphere
419 			b.vx = vx0;              b.vy  = vy0;      // initial velocity
420 			b1.omega=0;	
421 			b1.Fx=0;b1.Fy=0;		
422 			b1.x_ = b.x;              b1.y_  = b.y; 
423 			b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
424 			b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
425 			balls[n/2-(i+1)]=b;//[2*i]
426 			balls[n/2+(i)] = b1;//[2*i+1]
427 		}
428         context.clearRect(0, 0, w * scale, h * scale);      
429 	};
430 	
431 	slider_input_oy.oninput = function() {
432         sm_y = slider_input_oy.value;
433 		time = 1;
434 		j=1;
435 		for (i = 0;i<n/2;i++)
436 		{
437 			var b = [];
438 			var b1 = [];
439 			var time = 1;
440 			switch (f)
441 			{
442 				case 0:
443 					b.fi_x = ugol*j;
444 					b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);
445 					j=j*(-1);
446 					b1.fi_x = ugol*j; //corner with an axis OX
447 					b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
448 					break;
449 				case 1:
450 					if (i ==((n/2)-1))//fixing of edge
451 					{
452 						b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
453 						b.fi_x = 0;	
454 						b1.fi_x = ugol*j; //corner with an axis OX
455 						b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
456 					}
457 					else
458 					{
459 						b.fi_x = ugol*j;
460 						b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
461 						j=j*(-1);
462 						b1.fi_x = ugol*j; //corner with an axis OX
463 						b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
464 					}
465 					break;
466 				case 2:
467 					if (i ==((n/2)-1))//fixing of edges
468 					{
469 						b.x = (w / 2)-diag*(2*i+1)*1.0;          b.y = h / 2.0;
470 						b.fi_x = 0;	
471 						b1.x = (w / 2)+diag*(2*i+1)*1.0;          b1.y = h / 2.0;
472 						b1.fi_x = 0;
473 					}
474 					else
475 					{
476 						b.fi_x = ugol*j;
477 						b.x = (w / 2)-diag*(2*i+1)*(1.0+sm_x/100);          b.y = h / (2.00+sm_y/100);    // calculated coordinates of a sphere
478 						j=j*(-1);
479 						b1.fi_x = ugol*j; //corner with an axis OX
480 						b1.x = (w / 2)+diag*(2*i+1)*(1.0+sm_x/100);          b1.y = h / (2.00-sm_y/100) ;
481 					}
482 					break;
483 			}
484 			b.omega=0;//angular velocity
485 			var dx = diag*Math.cos(b.fi_x*Math.PI/180);//shift for drawing. 
486 			b.Fx=0;b.Fy=0;
487 			b.x_ = b.x;              b.y_  = b.y; 
488 			b.fx = 0;                b.fy  = 0;      // force operating on a sphere
489 			b.vx = vx0;              b.vy  = vy0;      // initial velocity
490 			b1.omega=0;	
491 			b1.Fx=0;b1.Fy=0;		
492 			b1.x_ = b.x;              b1.y_  = b.y; 
493 			b1.fx = 0;                b1.fy  = 0;      // force operating on a sphere
494 			b1.vx = vx0;              b1.vy  = vy0;      // initial velocity
495 			balls[n/2-(i+1)]=b;//[2*i]
496 			balls[n/2+(i)] = b1;//[2*i+1]
497 			
498 		}
499         context.clearRect(0, 0, w * scale, h * scale);      
500 	};
501 	 // The function doing spf of integration steps
502 	function physics() 
503 	{                    // the fact that there is each step of time
504 	    for (var s = 1; s <= spf; s++) //integration step
505 			{   
506 			
507 			for (i = 0;i<(n-1);i++)
508 			{   
509 				
510 				d =[];
511 				R = 1;
512 			    b = balls[i];//balls[2*i];
513 				b1 = balls[i+1];//balls[2*i+1];
514 				D = Math.sqrt((b.x-b1.x)*(b.x-b1.x)+(b.y-b1.y)*(b.y-b1.y));//Math.abs((b.x-b1.x));//Math.sqrt((b.x-b1.x)*(b.x-b1.x)+(b.y-b1.y)*(b.y-b1.y))-2*diag;
515 				d.fi_x = 180*Math.asin((b1.y-b.y)/D)/3.14;
516 				pr = 3.14/180;
517 				fi = 180+b1.fi_x
518 				
519 				//=============================================Силы=====================================
520 				A = -Math.cos(inRad(fi))*Math.cos(inRad(d.fi_x))-Math.sin(inRad(fi))*Math.sin(inRad(d.fi_x))+Math.cos(inRad(b.fi_x))*Math.cos(inRad(d.fi_x))+Math.sin(inRad(b.fi_x))*Math.sin(inRad(d.fi_x));
521 				b.Fx = B_1*(D-2*diag)*Math.cos(inRad(d.fi_x))+(B_2/2/D)*( Math.cos(inRad(fi))-Math.cos(inRad(b.fi_x))+A*Math.cos(inRad(d.fi_x)));
522 				b1.Fx = -b.Fx;
523 				b.Fy = B_1*(D-2*diag)*Math.sin(inRad(d.fi_x))+(B_2/2/D)*( Math.sin(inRad(fi))-Math.sin(inRad(b.fi_x))+A*Math.sin(inRad(d.fi_x)));
524 				b1.Fy = -b.Fy;
525 				M_tb = B_3*(Math.cos(inRad(fi))*Math.sin(inRad(b.fi_x))-Math.cos(inRad(b.fi_x))*Math.sin(inRad(fi)))-(B_4/2)*(Math.cos(inRad(fi-90))*Math.sin(inRad(b.fi_x+90))-Math.sin(inRad(fi-90))*Math.cos(inRad(b.fi_x+90)));
526 				b.fx = R * (b.Fy*Math.cos(inRad(b.fi_x))-b.Fx*Math.sin(inRad(b.fi_x))) - (B_2/2) * (Math.cos(inRad(d.fi_x))*Math.sin(inRad(b.fi_x))-Math.sin(inRad(d.fi_x))*Math.cos(inRad(b.fi_x))) + M_tb;
527 				b1.fx = R * (-Math.cos(inRad(fi))*b.Fy+Math.sin(inRad(fi))*b.Fx) + 	(B_2/2) * (Math.cos(inRad(d.fi_x))*Math.sin(inRad(fi))-Math.sin(inRad(d.fi_x))*Math.cos(inRad(fi)))- M_tb;
528 					
529 				//======================================================================================
530 				var J1 = 10000;
531 				var m =1;
532 				var beta_vr=0.00001//0.005;
533 				var beta_x=0.5//1;
534 				var beta_y=0.01//0.1;
535 				//console.log(c_b);
536 				if (f==0)//the free body
537 				{
538 					x_v1=balls[i].vx;
539 					y_v1=balls[i].vy;
540 					x_v2=balls[i+1].vx;
541 					y_v2=balls[i+1].vy;
542 					vr1 = balls[i].omega;
543 					vr2 = balls[i+1].omega;
544 					balls[i] = b;
545 					balls[i+1] = b1;
546 					balls[i].omega+=J1*(balls[i].fx-beta_vr*vr1)*dt;
547 					balls[i].vx+=m*(balls[i].Fx-beta_x*x_v1)*dt;
548 					balls[i].vy+=m*(balls[i].Fy-beta_y*y_v1)*dt;
549 					balls[i+1].omega+=J1*(balls[i+1].fx-beta_vr*vr2)*dt;
550 					balls[i+1].vx+=m*(balls[i+1].Fx-beta_x*x_v2)*dt;
551 					balls[i+1].vy+=m*(balls[i+1].Fy-beta_y*y_v2)*dt;
552 					balls[i].y+=balls[i].vy*dt;
553 					balls[i].fi_x+=balls[i].omega*dt;
554 					balls[i].x+=balls[i].vx*dt;
555 					balls[i+1].x+=balls[i+1].vx*dt;
556 					balls[i+1].fi_x+=balls[i+1].omega*dt;
557 					balls[i+1].y+=balls[i+1].vy*dt;
558 					asd=balls[0].fx+balls[1].fx;
559 				}
560 				else//the fixed edge
561 				{	
562 					if (f==1)////the fixed edge
563 					{
564 						balls[i] = b;
565 						balls[i+1] = b1;
566 						x_v1=balls[i].vx;
567 						y_v1=balls[i].vy;
568 						x_v2=balls[i+1].vx;
569 						y_v2=balls[i+1].vy;
570 						vr1 = balls[i].omega;
571 						vr2 = balls[i+1].omega;
572 						balls[i].omega+=J1*(balls[i].fx-beta_vr*vr1)*dt;
573 						balls[i].vx+=m*(balls[i].Fx-beta_x*x_v1)*dt;
574 						balls[i].vy+=m*(balls[i].Fy-beta_y*y_v1)*dt;
575 						balls[i+1].omega+=J1*(balls[i+1].fx-beta_vr*vr2)*dt;
576 						balls[i+1].vx+=m*(balls[i+1].Fx-beta_x*x_v2)*dt;
577 						balls[i+1].vy+=m*(balls[i+1].Fy-beta_y*y_v2)*dt;
578 						if (i>0)
579 						{
580 							balls[i].fi_x+=balls[i].omega*dt;
581 							balls[i+1].y+=balls[i+1].vy*dt;
582 							balls[i].y+=balls[i].vy*dt;
583 							balls[i].x+=balls[i].vx*dt;
584 							balls[i+1].x+=balls[i+1].vx*dt;
585 							balls[i+1].fi_x+=balls[i+1].omega*dt;
586 						}
587 					}
588 					else //both edges are fixed
589 					{
590 					
591 						x_v1=balls[i].vx;
592 						y_v1=balls[i].vy;
593 						x_v2=balls[i+1].vx;
594 						y_v2=balls[i+1].vy;
595 						vr1 = balls[i].omega;
596 						vr2 = balls[i+1].omega;
597 						balls[i] = b;
598 						balls[i+1] = b1;
599 						balls[i].omega+=J1*(balls[i].fx-beta_vr*vr1)*dt;
600 						balls[i].vx+=m*(balls[i].Fx-10*beta_x*x_v1)*dt;
601 						balls[i].vy+=m*(balls[i].Fy-10*beta_y*y_v1)*dt;
602 						balls[i+1].omega+=J1*(balls[i+1].fx-beta_vr*vr2)*dt;
603 						balls[i+1].vx+=m*(balls[i+1].Fx-10*beta_x*x_v2)*dt;
604 						balls[i+1].vy+=m*(balls[i+1].Fy-10*beta_y*y_v2)*dt;
605 						if ((i>0)&&(i<(n-2)))
606 						{
607 							balls[i].fi_x+=balls[i].omega*dt;
608 							balls[i+1].y+=balls[i+1].vy*dt;
609 							balls[i].y+=balls[i].vy*dt;
610 							balls[i].x+=balls[i].vx*dt;
611 							balls[i+1].x+=balls[i+1].vx*dt;
612 							balls[i+1].fi_x+=balls[i+1].omega*dt;
613 						}
614 						
615 					}
616 				}
617 				
618 			}
619 						
620 			time = time + 1;
621 		}
622 	}
623 	// definition of the function calculating force	
624 
625     // definition of function, risuyushchiy particle, walls and other
626     context.fillStyle = "#3070d0"; // colour
627 	//===================================Interaction by a mouse========================
628 	// function is started when pressing a key of a mouse
629     canvasBalls.onmousedown = function(e) {
630         var m = mouseCoords(e);                     // we receive cursor coordinates of a mouse
631         switch (f) 
632 		{
633 			case(0):
634 				var x = balls[n-1].x - m.x/scale;                           // distance from the center of a sphere to the cursor on an axis x
635 				var y = balls[n-1].y - m.y/scale;                           // distance from the center of a sphere to the cursor on an axis y
636 				var rLen2 = x * x + y * y;                  // distance square between the cursor and the center of a sphere
637 				if (rLen2 <= diag*diag) {                       // if the cursor pressed a sphere
638 					xShift = balls[n-1].x - m.x/scale;                      // shift of the cursor concerning the center of a sphere on x
639 					yShift = balls[n-1].y - m.y/scale;                      // shift of the cursor concerning the center of a sphere for y
640 					canvasBalls.onmousemove = mouseMove; // until the key is pressed - movement function works
641 				}
642 				break;
643 			case(1):
644 				var x = balls[n-1].x - m.x/scale;                           // distance from the center of a sphere to the cursor on an axis x
645 				var y = balls[n-1].y - m.y/scale;                           // distance from the center of a sphere to the cursor on an axis y
646 				var rLen2 = x * x + y * y;                  // distance square between the cursor and the center of a sphere
647 				if (rLen2 <= diag*diag) {                       // if the cursor pressed a sphere
648 					xShift = balls[n-1].x - m.x/scale;                      // shift of the cursor concerning the center of a sphere on x
649 					yShift = balls[n-1].y - m.y/scale;                      // shift of the cursor concerning the center of a sphere for y
650 					canvasBalls.onmousemove = mouseMove; // until the key is pressed - movement function works
651 				}
652 				break;
653 			case (2):
654 				case(0):
655 				var x = balls[n/2].x - m.x/scale;                           // distance from the center of a sphere to the cursor on an axis x
656 				var y = balls[n/2].y - m.y/scale;                           // distance from the center of a sphere to the cursor on an axis y
657 				var rLen2 = x * x + y * y;                  // distance square between the cursor and the center of a sphere
658 				if (rLen2 <= diag*diag) {                       // if the cursor pressed a sphere
659 					xShift = balls[n/2].x - m.x/scale;                      // shift of the cursor concerning the center of a sphere on x
660 					yShift = balls[n/2].y - m.y/scale;                      // shift of the cursor concerning the center of a sphere for y
661 					canvasBalls.onmousemove = mouseMove; // until the key is pressed - movement function works
662 				}
663 				break;
664 		}
665     };
666  
667     // function is started at a key release of a mouse
668     document.onmouseup = function() {
669         canvasBalls.onmousemove = null;        // when the key is released - there is no function of movement
670     };
671  
672     // function is started when moving a mouse (many times, at every moment of movement)
673     // in our case works only with a viced key of a mouse
674     function mouseMove(e) {
675 		switch (f)
676 		{
677 			case(0):
678 				var m = mouseCoords(e);                     // we receive cursor coordinates of a mouse
679 				balls[n-1].x = m.x/scale + xShift;
680 				balls[n-1].y = m.y/scale+ yShift;
681 				draw();
682 				break;
683 			case(1):
684 				var m = mouseCoords(e);
685 				x_nach =(w / 2)+diag*(n/2+2)*1.0;
686 				y_nach =  h / 2.0;
687 				r_nach = Math.sqrt(x_nach*x_nach+y_nach*y_nach);
688 				r_m = Math.sqrt(((m.x/scale-2*diag)-x_nach)*((m.x/scale-2*diag)-x_nach)+((m.y/scale)-y_nach)*((m.y/scale)-y_nach));
689 				console.log(x_nach);
690 				console.log(m.x/scale);
691 				//console.log(r_nach);
692 				if (Math.abs(r_m)<(3*diag))	// we receive cursor coordinates of a mouse
693 				{pr_x = m.x/scale + xShift*0.01 -balls[n-1].x;
694 				pr_y = m.y/scale+yShift-balls[n-1].y;
695 				balls[n-1].x = m.x/scale + xShift*0.0001;
696 				balls[n-1].y = m.y/scale+ yShift;
697 				}
698 				draw();
699 				break;
700 			case(2):
701 				var m = mouseCoords(e);                     // we receive cursor coordinates of a mouse				balls[n/2].x = m.x/scale + xShift;
702 				balls[n/2].y = m.y/scale+ yShift;
703 				draw();
704 				break;
705 		}
706     }
707  
708     // function returns cursor coordinates of a mouse
709     function mouseCoords(e) {
710         var m = [];
711         var rect = canvasBalls.getBoundingClientRect();
712         m.x = e.clientX - rect.left;
713         m.y = e.clientY - rect.top;
714 		//console.log(m.x/scale);
715 		//console.log(balls[n-1].x);
716         return m;
717     }
718 	
719 	function inRad(num) 
720 	{
721 		return num * Math.PI / 180;
722 	}
723 	
724     function draw() 
725 	{   				     
726          	context.clearRect(0, 0, w * scale, h * scale); // to clear the screen
727          	for (var i =0;i<n;i++)
728 			{	
729 			    b = balls[i];
730 				context.beginPath();
731 				context.translate(b.x*scale,b.y * scale);//transfer in the center 
732 				context.rotate(inRad(b.fi_x-45));
733 				context.fillRect(-rectW/2, -rectH/2, rectW, rectH);
734 				context.rotate(-inRad(b.fi_x-45));
735 				context.translate(-b.x * scale, -b.y * scale);//transfer back 
736 				context.closePath();
737 				context.stroke(); 
738 			}
739     }
740 }

File "v-model.html" 

 1  <!DOCTYPE html>
 2  <html>
 3  <head>
 4      <title> Particle </title>
 5      <script src="V_model.js"></script>
 6  </head>
 7  <body>
 8  	<!-- Addition of area for drawing of a particle -->
 9      <canvas id="canvasBalls" width="800" height="400" style="border:1px solid #000000;"></canvas>
10 	
11  	<div>
12 	    c_a =
13         <input id="Text_vx0" value = "100" style="width: 4.2ex;" required pattern="[-+]?([0-9]*\.[0-9]+|[0-9]+)" oninput="
14             if (!this.checkValidity()) return;
15             app.set_c_a(this.value);
16             <!-- document.getElementById('Slider_02').value = this.value; -->
17         ">
18 		<!-- Addition of a slider -->
19         <!-- <input type="range" id="Slider_02" style="width: 100px;" oninput="app.set_02(this.value); document.getElementById('Text_02').value = this.value;"> -->
20         </I></font>
21 	    c_b =
22         <input id="Text_vx0" value = "0.1" style="width: 4.2ex;" required pattern="[-+]?([0-9]*\.[0-9]+|[0-9]+)" oninput="
23             if (!this.checkValidity()) return;
24             app.set_c_b(this.value);
25             <!-- document.getElementById('Slider_02').value = this.value; -->
26         ">
27 		<!-- Addition of a slider -->
28         <!-- <input type="range" id="Slider_02" style="width: 100px;" oninput="app.set_02(this.value); document.getElementById('Text_02').value = this.value;"> -->
29         </I></font>
30 	    c_d =
31         <input id="Text_vx0" value = "100" style="width: 4.2ex;" required pattern="[-+]?([0-9]*\.[0-9]+|[0-9]+)" oninput="
32             if (!this.checkValidity()) return;
33             app.set_c_d(this.value);
34             <!-- document.getElementById('Slider_02').value = this.value; -->
35         ">
36 		<!-- Addition of a slider -->
37         <!-- <input type="range" id="Slider_02" style="width: 100px;" oninput="app.set_02(this.value); document.getElementById('Text_02').value = this.value;"> -->
38         </I></font>
39 	    c_t =
40         <input id="Text_vx0" value = "1" style="width: 4.2ex;" required pattern="[-+]?([0-9]*\.[0-9]+|[0-9]+)" oninput="
41             if (!this.checkValidity()) return;
42             app.set_c_t(this.value);
43             <!-- document.getElementById('Slider_02').value = this.value; -->
44         ">
45 		<!-- Addition of a slider -->
46         <!-- <input type="range" id="Slider_02" style="width: 100px;" oninput="app.set_02(this.value); document.getElementById('Text_02').value = this.value;"> -->
47         </I></font>
48 	<input type="button" name="" onclick="
49 	app.new_start();" value="restart"/></div>
50 	<div><input type="radio" id="radio_pic_1" name="pic" checked /> Free body
51     <input type="radio" id="radio_pic_2" name="pic" /> Fixed edge
52     <input type="radio" id="radio_pic_3" name="pic" /> Fixed edges <br></div>
53 	<div>Angle of torsion
54 	0
55 	<input type="range" id="slider_input" min=0 max=40 value=0 step=0.5 style="width: 200px;">40  
56 	<div>Shear OX
57 	0
58 	<input type="range" id="slider_input_ox" min=0 max=10 value=0 step=0.5 style="width: 200px;">10</div>
59 	<div>Shear OY 
60 	0
61 	<input type="range" id="slider_input_oy" min=0 max=10 value=0 step=0.5 style="width: 200px;">10</div>
62     <script type="text/javascript"> app = new MainParticle(document.getElementById('canvasBalls'));
63     </script>
64  </body>
65  </html>


Links[править]

Источник — «http://tm.spbstu.ru/?title=Particles_chain_with_V-model_interaction&oldid=46001»