Два математических маятника, связанных пружиной — различия между версиями
Vaan007 (обсуждение | вклад) |
Vaan007 (обсуждение | вклад) |
||
| Строка 18: | Строка 18: | ||
\right. | \right. | ||
</math> | </math> | ||
| + | <br /> | ||
| + | где <math>{k}_{1}=\sqrt\frac{{g}}{l}</math> и <math>{k}_{2}=\sqrt{\frac{{g}}{l} + \frac{{2Cd^2}}{ml^2}}</math> | ||
| + | <br /> | ||
| + | <math>\varphi_{1},\varphi_{2}</math> - обобщенные координаты | ||
| + | <br /> | ||
| + | <math>\varphi_{0}</math> - начальный угол отклонения | ||
| + | <br /> | ||
| + | <math>{g}</math> - гравитационная постоянная | ||
| + | <br /> | ||
| + | <math>{l}</math> - длина маятников | ||
| + | <br /> | ||
| + | <math>{m}</math> - масса маятников | ||
| + | <br /> | ||
| + | <math>{C}</math> - жесткость пружины | ||
| + | <br /> | ||
| + | <math>{d}</math> - положение пружина на стержне | ||
| + | <br /> | ||
{{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Alexandrov/TwoMaya.html |width=1000 |height=640 |border=0 }} | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Alexandrov/TwoMaya.html |width=1000 |height=640 |border=0 }} | ||
Версия 11:14, 5 июня 2015
Виртуальная лаборатория>Два математических маятника, связанных пружинойЧто собой представляет система
Два математических маятника, связанных пружиной, совершаю малый колебания. Упругое звено служит неким инструментом для "перекачки" энергии с одной пружины на другую.
Постановка задачи
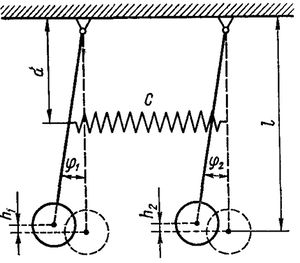
Математические маятники одинаковой длинны и массы совершают малые колебания. Пружина жесткости закреплена по центру стержней математических маятников. При отклонении первого маятника на малый угол под действием пружины происходит возбуждение колебаний второго маятника, а колебания первого затухают. Справедлив и обратный процесс.
Основные уравнения
где и
- обобщенные координаты
- начальный угол отклонения
- гравитационная постоянная
- длина маятников
- масса маятников
- жесткость пружины
- положение пружина на стержне