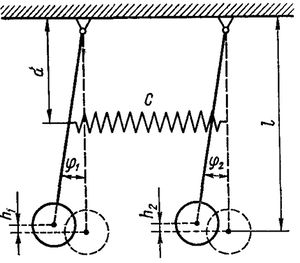
Два математических маятника, связанных пружиной
Материал из Department of Theoretical and Applied Mechanics
Виртуальная лаборатория>Два математических маятника, связанных пружиной
Что собой представляет система
Два математических маятника, связанные пружиной, совершают малые колебания. Упругое звено служит неким инструментом для "перекачки" энергии с одного маятника на другой.
Постановка задачи
Демонстрируются малые колебания математических маятников одинаковой длинны и массы . Пружина жесткости закреплена по центру стержней математических маятников. При отклонении первого маятника на малый угол под действием пружины происходит возбуждение колебаний второго маятника, а колебания первого затухают. Затем происходит обратный процесс.
Основные уравнения
где и
- обобщенные координаты
- начальный угол отклонения
- гравитационная постоянная
- длина маятников
- масса маятников
- жесткость пружины
- положение пружины на стержне
Скачать программу TwoMaya.rar.
Текст программы на языке JavaScript (разработчик Александров Сергей):
Файл "TwoMaya.js"
1 window.addEventListener("load", Main_Spring, true);
2 function Main_Spring() {
3
4 // *** Некие исходные данные ***
5
6 var canvas = spring_canvas;
7 canvas.onselectstart = function () {return false;}; // запрет выделения canvas
8 var ctx = canvas.getContext("2d"); // на ctx происходит рисование
9 var w = canvas.width; // ширина окна в расчетных координатах
10 var h = canvas.height; // высота окна в расчетных координатах
11
12 var Pi = 3.1415926; // число "пи"
13 var g = 9.8; // гравитационная постоянная
14
15 var T0 = 0.01; // масштаб времени (период колебаний исходной системы)
16 var k0 = 2 * Pi / T0; // масштаб частоты
17
18
19
20 var m0 = 1; // масштаб массы маятника
21 var l0 = 2; // масштаб длины маятника
22 var fiZero0 = 1; // масштаб начального угла отклонения
23 var d0 = 1; // масштаб местоположения пружины на маятнике
24 var C0 = 1; // масштаб жесткости пружины
25
26 var count = true; // проводить ли расчет системы
27 var v = 0; // скорость тела
28 var t = 0;
29 var f_1 = 0.1; // угл отклонения первого маятника от положения равновесия
30 var f_2 = 0.1; // угл отклонения второго маятника от положения равновесия
31 var q = 10; // маштабирующий коэффициент отклонения маятника
32
33 // параметры полученные из размеров холста
34 var rw = canvas.width / 100; var rh = canvas.height / 4;
35 //var x0 = (15 * rw - rw / 2); var y0 = (rh / 1.33 - rh / 2) * 10;
36 var x0 = canvas.width/5;
37 var y0 = canvas.height/8;
38 var rad0 = 15;
39
40 // параметры пружины
41 var coil = 10; // количество витков
42 var startX = 500; // закрепление пружины
43
44
45 // *** Задание вычислительных параметров ***
46
47 var fps = 60; // frames per second - число кадров в секунду (качечтво отображения)
48 var spf = 10; // steps per frame - число шагов интегрирования между кадрами
49 var dt = 50 * T0 / fps; // шаг интегрирования (качество расчета)
50 var steps = 0; // количество шагов интегрирования
51
52
53 // *** Задание физических параметров ***
54
55 var m = 1 * m0; // масса маятника
56 var C = 0.3 * C0; // жесткость пружины
57 var l = 8 * l0; // длина маятников
58 var fiZero = 0.3 * fiZero0; // начальное отклонение первого маятника
59 var d = l/2 * d0; // местоположение пружины на маятнике
60 var hole = canvas.width/2 + 50; // расстояние между закреплениями маятников по Х
61 var bound_x = x0; // координаты закрепления первого маятника по Х
62 var bound_y = 10; // координаты закрепления первого маятника по У
63
64 slider_m.value = (m / m0).toFixed(1); number_m.value = (m / m0).toFixed(1);
65 slider_C.value = (C / C0).toFixed(1); number_C.value = (C / C0).toFixed(1);
66 slider_l.value = (l / l0).toFixed(1); number_l.value = (l / l0).toFixed(1);
67 slider_fiZero.value = (fiZero / fiZero0).toFixed(1); number_fiZero.value = (fiZero / fiZero0).toFixed(1);
68 slider_spf.value = (spf).toFixed(1); number_spf.value = (spf).toFixed(1);
69
70 // *** Установка слайдеров для переменных величин ***
71
72 function setM(new_m) {m = new_m * m0;}
73 function setC(new_C) {C = new_C * C0;}
74 function setL(new_l) {l = new_l * l0;}
75 function setFiZero(new_fiZero) {fiZero = new_fiZero * fiZero0;}
76 function setSpf(new_spf) {spf = new_spf;}
77
78 slider_m.oninput = function() {number_m.value = slider_m.value; setM(slider_m.value);};
79 number_m.oninput = function() {slider_m.value = number_m.value; setM(number_m.value);};
80
81 slider_C.oninput = function() {number_C.value = slider_C.value; setC(slider_C.value);};
82 number_C.oninput = function() {slider_C.value = number_C.value; setC(number_C.value);};
83
84 slider_l.oninput = function() {number_l.value = slider_l.value; setL(slider_l.value);};
85 number_l.oninput = function() {slider_l.value = number_l.value; setL(number_l.value);};
86
87 slider_fiZero.oninput = function() {number_fiZero.value = slider_fiZero.value; setFiZero(slider_fiZero.value);};
88 number_fiZero.oninput = function() {slider_fiZero.value = number_fiZero.value; setFiZero(number_fiZero.value);};
89
90 slider_spf.oninput = function() {number_spf.value = slider_spf.value; setSpf(slider_spf.value);};
91 number_spf.oninput = function() {slider_spf.value = number_spf.value; setSpf(number_spf.value);};
92
93
94 // Параметры первого круга-грузика
95 var circ1 = {
96 x: x0,
97 y: y0,
98 rad: rad0,
99 fill: "rgba(0, 0, 255, 1)"
100 };
101
102 // Параметры второго круга-грузика
103 var circ2 = {
104 x: x0+hole,
105 y: y0,
106 rad: rad0,
107 fill: "rgba(0, 255, 0, 1)"
108 };
109
110 // *** Функция обеспечивающая "жизнь" маятников с пружиной ***
111
112 function control() {
113 calculate();
114 draw();
115 requestAnimationFrame(control);
116
117 }
118 control();
119
120 // график
121 var vGraph1 = new TM_graph( // определить график
122 "#vGraph1", // на html-элементе #vGraph
123 250, // сколько шагов по оси "x" отображается
124 -1, 1, 0.1); // мин. значение оси Y, макс. значение оси Y, шаг по оси Y
125
126 var vGraph2 = new TM_graph( // определить график
127 "#vGraph2", // на html-элементе #vGraph
128 250, // сколько шагов по оси "x" отображается
129 -1, 1, 0.1); // мин. значение оси Y, макс. значение оси Y, шаг по оси Y
130
131
132
133 // *** Функция расчетов координат ***
134
135 function calculate() {
136
137 //if (!count) return;
138
139 for (var s=1; s<=spf; s++) {
140
141 var k1 = Math.sqrt(g/l); // коэффициент первой пружины
142 var k2 = Math.sqrt(g/l + (2 * C * Math.pow(d,2))/m/(Math.pow(l,2))); // коэффициент второй пружины
143
144 t += dt;
145
146 f_1 = fiZero * Math.cos((k1 + k2)/2 * t) * Math.cos((k1 - k2)/2 * t); // закон изменения угла отклонения первого маятника от положения равновесия
147 f_2 = fiZero * Math.sin((k1 + k2)/2 * t) * Math.sin((k2 - k1)/2 * t); // закон изменения угла отклонения второго маятника от положения равновесия
148
149
150 // изменение координат первого грузика
151 circ1.x = (x0 + l * Math.sin(f_1) * q);
152 circ1.y = 100 + (y0 + l * Math.cos(f_1) * q);
153
154 // изменение координат второго грузика
155 circ2.x = (x0 + hole + l * Math.sin(f_2) * q);
156 circ2.y = 100 + (y0 + l * Math.cos(f_2) * q);
157
158
159 steps++;
160 if (steps % 80 == 0) {
161 vGraph1.graphIter(steps, (f_1))
162 vGraph2.graphIter(steps, (f_2))}; // подать данные на график
163 }
164
165 }
166
167 // *** Функция рисования объектов ***
168
169 function draw() {
170
171 ctx.clearRect(0, 0, w, h);
172
173
174 //!!! пружина
175 /* draw_spring(
176 100, // х-координата начала пружины
177 400, // х-координата конца пружины
178 300, // у-координата пружины
179 6, // количество витков пружины
180 100 // высота изгиба пружины (чем меньше, тем больше пружина похожа на линию)
181 ); */
182
183 // Пружина соединяющая два маятника
184 draw_spring((circ1.x - x0)/2 + x0, (circ2.x - x0 - hole)/2 + x0 + hole , (circ1.y + y0/2)/2 , 10, 30);
185
186
187 // Стержень первого маятника
188 ctx.lineWidth = 6;
189 ctx.strokeStyle = "#e1974d";
190 ctx.beginPath();
191 ctx.moveTo(circ1.x, circ1.y);
192 ctx.lineTo(x0, y0 - bound_y);
193 ctx.stroke();
194
195 // Стержень второго маятника
196 ctx.lineWidth = 6;
197 ctx.strokeStyle = "#e1974d";
198 ctx.beginPath();
199 ctx.moveTo(circ2.x, circ2.y);
200 ctx.lineTo(x0 + hole,y0 - bound_y);
201 ctx.stroke();
202
203 // Круглый грузик первого маятника
204 ctx.beginPath();
205 ctx.arc(circ1.x, circ1.y, rad0, 0, 2 * Math.PI, false);
206 ctx.fillStyle = 'red';
207 ctx.fill();
208 ctx.lineWidth = 7;
209 ctx.strokeStyle = '#003300';
210 ctx.stroke();
211
212 // Круглый грузик второго маятника
213 ctx.beginPath();
214 ctx.arc(circ2.x, circ2.y, rad0, 0, 2 * Math.PI, false);
215 ctx.fillStyle = 'blue';
216 ctx.fill();
217 ctx.lineWidth = 7;
218 ctx.strokeStyle = '#003300';
219 ctx.stroke();
220
221 // Рисование закрепления первого маятника
222 ctx.lineWidth = 6;
223 ctx.strokeStyle = "#7394cb";
224 ctx.beginPath();
225 ctx.moveTo(x0-20, y0 - bound_y);
226 ctx.lineTo(x0+20, y0 - bound_y);
227 ctx.stroke();
228
229 // Рисование закрепления второго маятника
230 ctx.lineWidth = 6;
231 ctx.strokeStyle = "#7394cb";
232 ctx.beginPath();
233 ctx.moveTo(x0-20 + hole, y0 - bound_y);
234 ctx.lineTo(x0+20 + hole, y0 - bound_y);
235 ctx.stroke();
236 }
237
238 // *** Функция рисования пружины ***
239
240 function draw_spring(x_start, x_end, y, n, h) {
241 ctx.lineWidth = 2;
242 ctx.strokeStyle = "#7394cb";
243 var L = x_end - x_start;
244 for (var i = 0; i < n; i++) {
245 var x_st = x_start + L / n * i;
246 var x_end = x_start + L / n * (i + 1);
247 var l = x_end - x_st;
248 ctx.beginPath();
249 ctx.bezierCurveTo(x_st, y, x_st + l / 4, y + h, x_st + l / 2, y);
250 ctx.bezierCurveTo(x_st + l / 2, y, x_st + 3 * l / 4, y - h, x_st + l, y);
251 ctx.stroke();
252 }
253 }
254 }
