Моделирование динамики толпы в областях со сложной геометрией — различия между версиями
Денис (обсуждение | вклад) (→Самое интересное) |
(→Ссылки) |
||
| (не показаны 24 промежуточные версии 1 участника) | |||
| Строка 2: | Строка 2: | ||
Научный руководитель: [[Антон_Кривцов|Кривцов А. М.]] | Научный руководитель: [[Антон_Кривцов|Кривцов А. М.]] | ||
| + | |||
| + | Презентация: [[media: Presentation7.ppt|Моделирование динамики толпы]] | ||
== Введение == | == Введение == | ||
| − | В работе исследуются способы | + | В работе исследуются способы оптимизации движения людей, особенно в условиях паники — ведь в таком случае появляется большой риск получения людьми увечий вследствие увеличения «давления» в толпе. |
| − | Актуальность данной проблемы подтверждается, например, событиями в 2010 году в Дуйсбурге на фестивале «Love Parade», в ходе которого образовалась давка, в результате которой погиб 21 человек, и было ранено около 500 человек. | + | Толпа — бесструктурное скопление людей, лишенных ясно осознаваемой общности целей, но взаимно связанных сходством эмоционального состояния и общим объектом внимания. <ref name="def"/> |
| + | |||
| + | Давка — Скопление теснящихся в беспорядке, давящих друг на друга людей. <ref name="def2"/> Давка может привести к получению увечий людьми, поэтому движение должно быть организовано так, чтобы обеспечить умеренное «давление» в толпе. | ||
| + | |||
| + | Актуальность данной проблемы подтверждается, например, событиями в 2010 году в Дуйсбурге на фестивале «Love Parade», в ходе которого образовалась давка, в результате которой погиб 21 человек, и было ранено около 500 человек. <ref name="LP"/> | ||
== Цель == | == Цель == | ||
| − | Цель работы | + | Цель работы — разработать математическую модель и с её помощью исследовать движение толпы при различных условиях, найти лучшие способы организации движения в таких местах, как проход в метрополитен, фойе театра, проход в концертный зал, и в других местах, предполагающих переход большого количества людей через некий узкий проём. |
| + | |||
| + | Данный вопрос рассматривается в книге <ref name="book"/>, а также в исследованиях группы «GAMMA research group» и некоторых других исследованиях, однако до сих пор нет ясности, как распределяется давление в толпе и как влияет геометрия прохода на время прохождения толпы. | ||
| + | |||
| + | В работе <ref name="cellular"/> для моделирования толпы людей, а также препятствий на их пути, используется клеточный автомат на основе окрестности фон Неймана. Всё пространство делится на “клетки”, состояние каждой клетки определяется её соседями, а также состоянием клетки на предыдущем шаге. Данная модель достаточно проста в реализации, однако, с её помощью трудно достаточно точно определить время, требуемое для прохождения толпой определенного препятствия. | ||
== Реализация == | == Реализация == | ||
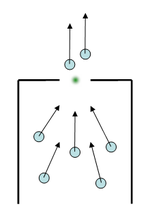
[[Файл: MDC_vect_field.png|150px|thumb|right|Векторное поле модели]] | [[Файл: MDC_vect_field.png|150px|thumb|right|Векторное поле модели]] | ||
Для моделирования данной задачи используется программа, написанная на языке Java с использованием библиотеки OpenGL. | Для моделирования данной задачи используется программа, написанная на языке Java с использованием библиотеки OpenGL. | ||
| − | Для описания взаимодействия частиц (людей) используется положительная часть потенциала Леннарда-Джонса | + | |
| − | + | Java - Объектно-ориентированный язык программирования. Приложения Java могут работать на любой виртуальной Java-машине (JVM) независимо от компьютерной архитектуры. | |
| + | |||
| + | OpenGL (Open Graphics Library — открытая графическая библиотека) — спецификация, определяющая независимый от языка программирования программный интерфейс для написания приложений, использующих двумерную и трёхмерную компьютерную графику. | ||
| + | |||
| + | Для описания взаимодействия частиц (людей) между собой (или со стенками геометрии) используется положительная часть потенциала Леннарда-Джонса <ref name="LJ"/> — частицы отталкиваются друг от друга (или от стенок), но не притягиваются: | ||
| + | |||
| + | <math>U_p (r) = \left\{ \begin{gathered} U(r), U(r)\ge 0 \hfill \\ 0, U(r)<0 \hfill \\ \end{gathered} \right.</math> | ||
| + | |||
| + | |||
| + | |||
---- | ---- | ||
| Строка 113: | Строка 132: | ||
[[MDCrowd_White_hall|Геометрия белого зала]], 90 частиц, модель человека | [[MDCrowd_White_hall|Геометрия белого зала]], 90 частиц, модель человека | ||
| − | [[Файл: MDC_1.7.0- | + | [[Файл: MDC_1.7.0-x300w.gif]] |
| + | |||
| + | {{#widget:YouTube|id=VjZEgjfEvcQ}} | ||
| + | |||
| + | [[media: MDC_1.7.0w.avi|Скачать видео]] | ||
| + | |||
[[Файл: MDC_Anim500.gif]] | [[Файл: MDC_Anim500.gif]] | ||
| − | {{#widget:YouTube|id= | + | {{#widget:YouTube|id=1N2bIw0QRWE}} |
| + | |||
| + | [[media: MDC_White_hall.avi|Скачать видео]] | ||
| + | |||
| + | == Список использованной литературы== | ||
| + | |||
| + | <references> | ||
| + | <ref name="def"> [http://vocabulary.ru/dictionary/852/word/tolpa Психологический лексикон. Энциклопедический словарь в шести томах] | ||
| + | </ref> | ||
| + | <ref name="def2"> [http://dic.academic.ru/dic.nsf/ogegova/44126 Толковый словарь Ожегова] </ref> | ||
| + | <ref name="LP"> [http://ru.wikipedia.org/wiki/Парад_любви Love Parade] </ref> | ||
| + | <ref name="book">Холщевников В. В., Самошин Д. А. Эвакуация и поведение людей при пожарах: Учеб. пособие. — М.: Академия ГПС МЧС России, 2009. — 212 с.</ref> | ||
| + | <ref name="cellular">Степанцов М.Е. Математическая модель направленного движения группы людей // Математическое моделирование, 2004, т.16, №3, с. 43-49</ref> | ||
| + | <ref name="LJ">Кривцов А. М. Деформирование и разрушение твердых тел с микроструктурой. — М.: ФИЗМАТЛИТ, 2007. — 304 с.</ref> | ||
| + | |||
| + | </references> | ||
| + | |||
| + | == Благодарности == | ||
| + | *[[Вита Денисова]] | ||
| + | *[[Виталий Кузькин]] | ||
| − | == | + | == См. также == |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | * [[Моделирование динамики толпы]] | |
| − | *[[ | ||
| − | |||
| − | |||
Текущая версия на 14:18, 26 июля 2014
Выполнил: Цветков Д. В.
Научный руководитель: Кривцов А. М.
Презентация: Моделирование динамики толпы
Содержание
Введение[править]
В работе исследуются способы оптимизации движения людей, особенно в условиях паники — ведь в таком случае появляется большой риск получения людьми увечий вследствие увеличения «давления» в толпе.
Толпа — бесструктурное скопление людей, лишенных ясно осознаваемой общности целей, но взаимно связанных сходством эмоционального состояния и общим объектом внимания. [1]
Давка — Скопление теснящихся в беспорядке, давящих друг на друга людей. [2] Давка может привести к получению увечий людьми, поэтому движение должно быть организовано так, чтобы обеспечить умеренное «давление» в толпе.
Актуальность данной проблемы подтверждается, например, событиями в 2010 году в Дуйсбурге на фестивале «Love Parade», в ходе которого образовалась давка, в результате которой погиб 21 человек, и было ранено около 500 человек. [3]
Цель[править]
Цель работы — разработать математическую модель и с её помощью исследовать движение толпы при различных условиях, найти лучшие способы организации движения в таких местах, как проход в метрополитен, фойе театра, проход в концертный зал, и в других местах, предполагающих переход большого количества людей через некий узкий проём.
Данный вопрос рассматривается в книге [4], а также в исследованиях группы «GAMMA research group» и некоторых других исследованиях, однако до сих пор нет ясности, как распределяется давление в толпе и как влияет геометрия прохода на время прохождения толпы.
В работе [5] для моделирования толпы людей, а также препятствий на их пути, используется клеточный автомат на основе окрестности фон Неймана. Всё пространство делится на “клетки”, состояние каждой клетки определяется её соседями, а также состоянием клетки на предыдущем шаге. Данная модель достаточно проста в реализации, однако, с её помощью трудно достаточно точно определить время, требуемое для прохождения толпой определенного препятствия.
Реализация[править]
Для моделирования данной задачи используется программа, написанная на языке Java с использованием библиотеки OpenGL.
Java - Объектно-ориентированный язык программирования. Приложения Java могут работать на любой виртуальной Java-машине (JVM) независимо от компьютерной архитектуры.
OpenGL (Open Graphics Library — открытая графическая библиотека) — спецификация, определяющая независимый от языка программирования программный интерфейс для написания приложений, использующих двумерную и трёхмерную компьютерную графику.
Для описания взаимодействия частиц (людей) между собой (или со стенками геометрии) используется положительная часть потенциала Леннарда-Джонса [6] — частицы отталкиваются друг от друга (или от стенок), но не притягиваются:
Для более наглядного отображения результатов моделирования разработаны средства визуализации, позволяющие отобразить достаточное количество частиц и требуемую геометрию области.
Для оценки ситуации измеряются две величины – время прохождения частиц через отверстие, и давление, возникающее в группе частиц. Требуется достичь минимального времени, однако при этом давление не должно превышать некоторого критического значения – чтобы максимально снизить риск травмирования людей в толпе.
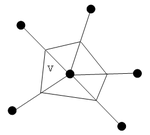
Для расчета давления в системе, используется формула из главы «Техника моделирования» книги А. М. Кривцова «Деформирование и разрушение твердых тел с микроструктурой».
где d – размерность задачи (в нашем случае d = 2),
Fα - воздействие на частицу от окружающих её частиц α,
Aα – расстояние от рассчитываемой частицы до окружающих её частиц,
V – собственное пространство частицы (площадь многоугольника, построенного на половинах расстояний до ближайших частиц)
Для визуализации давлений, действующих на частицу, используется цвет этой частицы – чем больше давление, тем больше смещение к красному концу спектра
Также есть режим демонстрации. В этом режиме вместо сферы используется модель человека, взятая с сайта 3dmodelfree.com. Шаги модели анимированы с использованием системы 3Ds Max, а повороты и скорость шага смоделированы с помощью специально разработанной программной системы визуализации.
Сбор результатов расчетов[править]
После каждого расчета полученные в ходе расчета данные записываются в файл результатов.
Программа может последовательно изменять какие-либо параметры начальной системы – например, можно задать начальное количество частиц – 30, конечное – 60 и шаг – 10. Тогда в автоматическом режиме будут посчитаны системы для 30, 40, 50 и 60 частиц, и после каждого расчета в файл результатов будут добавлены результаты эксперимента (время, затраченное частицами на «выход из комнаты», давления, возникающие в системе.) и его начальные условия. Таким же образом можно изменять и другие параметры – ширину прохода, количество расчетов одной системы, и др.
Для ускорения расчета ресурсоемких систем сделан режим запуска программы без визуализации, также предполагается сделать запись каждого шага в файл, чтобы можно было подробнее рассматривать шаги решения уже рассчитанной системы.
Результаты[править]
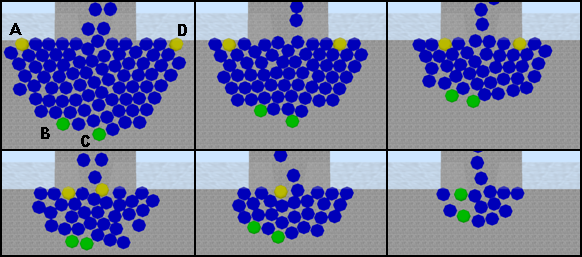
I. Время прохождения частиц в зависимости от начального положения.
Проведен ряд экспериментов, в ходе которых установлено, что отдельные частицы, находящиеся в точках A и D (см. рисунок), достигают прохода примерно на 25-30% быстрее, чем частицы, находящиеся в точках B и C.
Данные результаты близки к результатам исследований, проведенных В. А. Денисовой в работе «Моделирование социальных процессов», где был проведен и снят на видеокамеру ряд экспериментов у метро «Василеостровская»
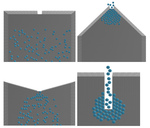
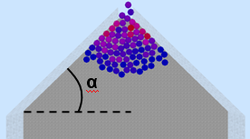
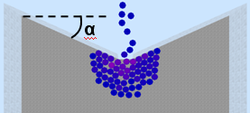
II. Время прохождения частиц в зависимости от геометрии прохода.
Проведены эксперименты, измеряющие зависимость скорости преодоления частицами прохода в зависимости от геометрии прохода. Единицей измерения времени в данном эксперименте взят шаг интегрирования N. В качестве изменяемой величины геометрии прохода взят угол наклона α стенок у прохода.
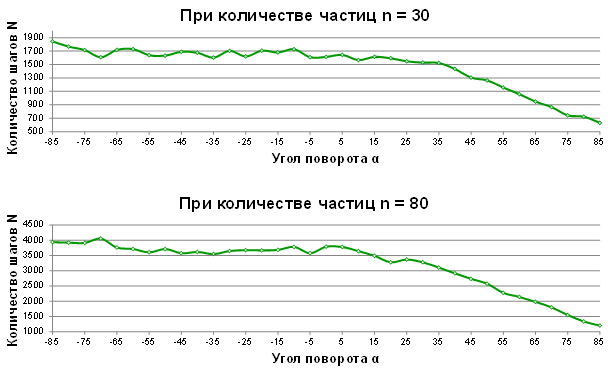
Эксперименты проводились в автоматическом режиме с выводом значений в файл. Для каждого угла α проведено 5 экспериментов, и проведено усреднение.
Результаты:
Видно, что при угле поворота от -85° до 15° время преодоления прохода практически одинаково, а при больших углах это время уменьшается с линейной зависимостью. Однако, визуально можно заметить, что при α < 0 давление у входа много меньше, чем при α > 0.
В предельной ситуации (при α = -90°) получаются вертикальные бортики, которые используются у входа некоторых станций метрополитена.
Самое интересное[править]
Здесь можно запустить саму программу в различных конфигурациях и посмотреть, как она работает. Чтобы запустить программу, нужно иметь установленный JRE (JAVA), скачать его можно отсюда [1]
Квадратная геометрия, 60 частиц, модель человека
Расширяющаяся геометрия, 60 частиц, модель шара
Сужающаяся геометрия, 60 частиц, модель шара
Геометрия с бортиками, 40 частиц, модель шара
Геометрия белого зала, 90 частиц, модель человека
Список использованной литературы[править]
- ↑ Психологический лексикон. Энциклопедический словарь в шести томах
- ↑ Толковый словарь Ожегова
- ↑ Love Parade
- ↑ Холщевников В. В., Самошин Д. А. Эвакуация и поведение людей при пожарах: Учеб. пособие. — М.: Академия ГПС МЧС России, 2009. — 212 с.
- ↑ Степанцов М.Е. Математическая модель направленного движения группы людей // Математическое моделирование, 2004, т.16, №3, с. 43-49
- ↑ Кривцов А. М. Деформирование и разрушение твердых тел с микроструктурой. — М.: ФИЗМАТЛИТ, 2007. — 304 с.