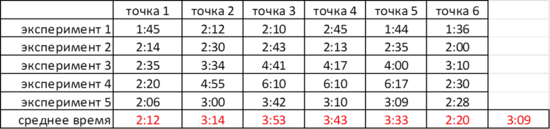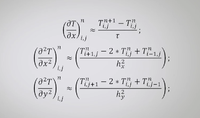Моделирование динамики толпы
Выполнил: Денисова Вита
Научный руководитель: Кривцов А.М., Кузькин В.А.
Введение[править]
В истории всегда существовал довольно большой интерес к попытке понять и управлять движением и поведением больших групп людей. Зачастую поведение толпы исследовалось в рамках социологии и психологии с целью исследования событий, случающихся в группах людей, объединенных общей целью, и функционирующих как единое целое. В таких случаях люди начинают частично терять свою индивидуальность и совершать поступки в рамках общего поведения толпы.
Толпа – бесструктурное скопление людей, лишенных ясно осознаваемой общности целей, но взаимно связанных сходством эмоционального состояния и общим объектом внимания.
Паника – эмоциональное состояние, возникающее как следствие или дефицита информации о какой-то ситуации, или ее чрезмерного избытка и проявляющееся в импульсивных действиях.
С ростом населения крупных городов, исследования поведения массовых скоплений людей в последнее время становятся все важнее. Следующие проблемы могут быть решены только на основе математического моделирования толпы:
- оптимизация пропускной способности транспортных систем;
- действия толпы в экстремальных ситуациях (например, пожар или террористический акт);
- создание поведенчески-реалистичных виртуальных толп в компьютерной графике в кино и играх.
Разработкой и усовершенствованием моделей, методов и средств компьютерного моделирования толпы занимаются многие отечественные и зарубежные исследователи, среди которых В.М. Предтеченский, М.Я. Ройтман, В.В. Холщевников, С.В. Беляев, А.Н. Овсянников, Д. Толлман (D. Thallmann), С. Мусс (S. Musse), Д. Терзопулос (D. Terzopoulos), Д. Хелбинг (D. Helbing), Р. Хагс (R. Hughes), А. Трюи (A. Treuille), С. Рейнолдс (C. Reynolds) и др.
Сущность толпы можно трактовать несколькими методами, но среди всех исследований на эту тему существует два подхода:
- дискретный
- континуальный
В первом толпа представляется в качестве совокупности множества независимых элементов, каждый из которых действует на основании каких-либо правил. В континуальном случае толпа рассматривается либо как жидкость, подчиняющаяся и описываемая гидро- и газодинамическими законами (например, уравнениями Бернулли или Навье-Стокса), либо в форме другой сплошной среды.
На основании данных подходов существует множество методов создания моделей поведения толпы, и их можно разделить на несколько классов:
- Методы на основе клеточных автоматов. В подобных методах пространство, по которому перемещаются агенты, представляется в виде набора клеток, образующих некоторую периодическую решетку с заданными правилами перехода, определяющими состояние клетки в следующий момент времени через состояние клеток, находящимися от нее на расстоянии не больше некоторого, в текущий момент времени
- Методы на основе физических процессов динамики жидкости. В данном случае каждый элемент толпы представляет собой частицу, состояние которой описывается уравнениями динамики жидкости (например, уравнениями Навье-Стокса)
- Методы на основе ньютоновской механики. В подобных методах все социальные силы, действующие на агента в толпе, выражаются в виде сил. Движение агента же описывается на основе второго закона Ньютона
- Мультиагентные методы. В соответствии с этим подходом, в процессе моделирования не описывается динамическая система в целом, а создается набор элементарных правил, которым подчиняется любой агент в толпе.
- Методы, основанные на данных, полученных из реальных наблюдений за поведением толп в различных условий. Зачастую подобные методы имеют узкую направленность (применимы, например, только для моделирования пожарной эвакуации).
- Гибридные методы, использующие комбинацию нескольких вышеперечисленных подходов.
Моделирование поведения толпы позволяет разработать рекомендации специалистам, помогающие обеспечивать высокий уровень безопасности в обыденных и экстремальных ситуациях, оптимизировать различные здания и сооружения с точки зрения эффективности прохождения людского потока, а также эффективно управлять транспортным потоком.
Целью работы является исследование поведения толпы для оптимизации движения в местах скопления людей.
Объект исследования
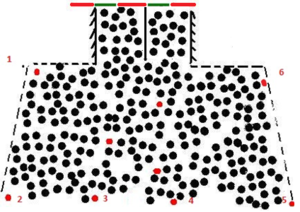
Поведение толпы на станция «Василеостровская» Петербургского метрополитена, где из-за особенностей проектирования и строительства станции существуют ограничения на вход-выход и, как следствие, давка в час-пик.
Эксперимент[править]
Суть эксперимента: толпа людей входила в метро на станции в час-пик. В эксперименте принимали участие студенты, которые выделялись из толпы наличием красных шапочек на голове. Каждый из них засекал время. Процесс продвижения толпы к входу в метро снимался на фото и видео-камеру.
Задача эксперимента заключалась в измерении времени, которое потребуется, чтобы зайти в здание метро, нахождении оптимальных точек начала движения, определении пропускной способности каждой двери.
Результаты эксперимента:
Среднее время 3:09
Наибольшее время 6:17 (5)
Лучшее время 1:36 (6)
Пропускная способность:
левая дверь – 67 чел/мин
правая дверь – 77 чел/мин
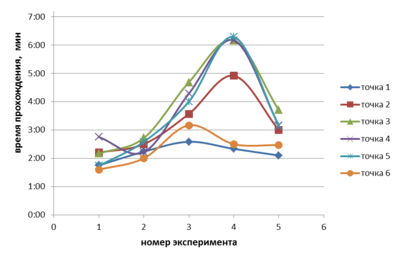
- Во время четвертого эксперимента был самый «час-пик»
- Точка 1 и точка 6 – самые выгодные места начала движения
- В правом коридоре при большей пропускной способности время прохождения тоже больше, это явление объясняется появление случайных людей с боку (со Среднего пр.), перелезающих через ограждение, которые не тратят время на прохождение всего пути, но несколько увеличивают среднее время прохождения.
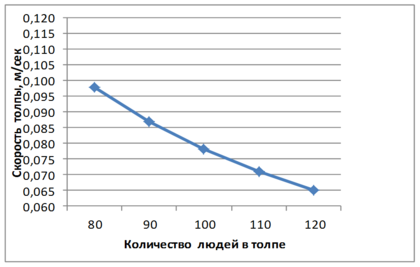
, где N −количество людей в толпе, f − площадь проекции человека (м2), б – ширина (м), l – длина толпы (м)
Зная среднюю пропускную способность Q из эксперимента , можно посчитать скорость толпы.
Полученные результаты близки к исследованиям Д. В. Цветкова, в своей работе Моделирование динамики толпы в областях со сложной геометрией он получил, что отдельные частицы, находящиеся в точках A и D (1 и 6 в данной работе), достигают прохода примерно на 25-30% быстрее, чем частицы, находящиеся в точках B и C (2 и 3)
Моделирование[править]
Использовался метод динамики частиц, язык программирования С#.
Конечная толпа, n – частиц, взаимодействующих между собой с силой
Частицы взаимодействуют со стенками по аналогичному закону, но с другой контактной жесткостью.
Внешняя силы в направлении выхода
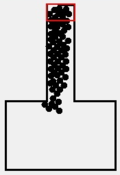
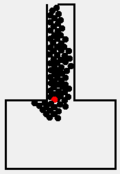
Результаты моделирования
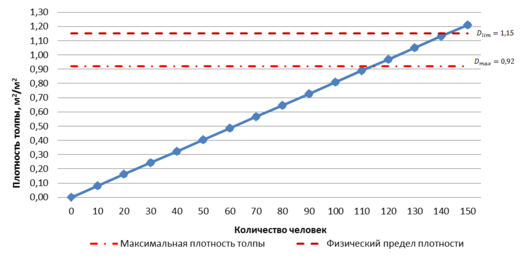
- В геометрии 1 D=0,79м2/м2 в выделенной области, а геометрии 2 плотность толпы превышает физический предел, поэтому не смотря на то что среднее время прохождения геометрии 1 больше, это форма безопаснее, т.е. геометрия 1 (c вертикальными ограждениями) является оптимальной, что сходится с аналитическими расчетами.
- Среднее время прохождения частицей 2:55, что совпадает с экспериментальными результатами с погрешностью не > 8%
Заключение[править]
В результате проделанной работы:
- Определены точки – наиболее выгодные места начала движения по результатам эксперимента
- Построена модель, имитирующая движение толпы в заданном пространстве, позволяющая вычислять время, скорости, плотность и др. показатели толпы
- Определена оптимальная форма геометрии объекта
- Результаты моделирования сходятся с экспериментальными данными и аналитическими расчетами и другими работами.
Направления дальнейших исследований
- Усовершенствование написанной программы, усложнение геометрии, увеличение количества входов/выходов, внедрение индивидуального, нестандартного поведения частиц
- Исследование других объектов, сравнение данных модели и эксперимента
Презентации[править]
- 14 октября 2012. В. Денисова. Моделирование социальных процессов. Научный руководитель В.А. Кузькин. Скачать презентацию, pptx: 721 kb
- 16 марта 2012. В. Денисова. Моделирование динамики поведения толпы. Подробнее. Научный руководитель В.А. Кузькин. Скачать презентацию, pptx: 5745 kb
- 11 мая 2012. В. Денисова. Моделирование социальных процессов. Научный руководитель В.А. Кузькин. Скачать презентацию, pptx: 7875 kb
СМИ[править]
См. также[править]
- Моделирование динамики толпы в областях со сложной геометрией
- Турбулентность толпы: согласно исследованиям ученых из технологического института в Цюрихе причинами гибели людей в давке на Love Parade в Дуйсбурге являлись не паника или массовое бегство, а турбулентные процессы в толпе при превышении критической плотности.
- Толпа металлистов - идеальный газ? (скачать статью из ArXive)
- Crowd and Multi-agent Simulation