КП: Тензор жесткости кристалла — различия между версиями
(→Решение) |
(→Решение) |
||
| Строка 38: | Строка 38: | ||
== Решение == | == Решение == | ||
''Первый этап'' | ''Первый этап'' | ||
| + | |||
Нахождение тензора жесткости второго порядка для плоской задачи, при равномерном радиальном расположении пружин одинаковой жесткости. | Нахождение тензора жесткости второго порядка для плоской задачи, при равномерном радиальном расположении пружин одинаковой жесткости. | ||
| + | |||
| + | <math>\sum^{n}_{i=0} {c_{i}e_{i}e_{i}}</math> | ||
| + | |||
| + | Результат: | ||
| + | <math>C = \frac{cn} {2} E </math> - общая формула, для нахождения тензора жесткости в этом случае, где Е -плоский единичный тензор 2-го ранга. | ||
''Второй этап'' | ''Второй этап'' | ||
| + | |||
Нахождение тензора жесткости 2-го, 3-го и 4-го порядков для основных типов кристаллических решеток.(ОЦК, ГЦК, Кубическая) | Нахождение тензора жесткости 2-го, 3-го и 4-го порядков для основных типов кристаллических решеток.(ОЦК, ГЦК, Кубическая) | ||
Версия 23:06, 27 мая 2013
А.М. Кривцов > Теоретическая механика > Курсовые проекты 2013 > Тензор жесткости кристалла
Курсовой проект по Теоретической механике
Исполнитель: Ванюшкина Валентина
Группа: 07 (20510)
Семестр: весна 2013
Содержание
Аннотация проекта
Проект посвящен тензору жесткости в кристаллах.
Постановка задачи
Необходимо вывести формулу тензора жесткости для наиболее часто-встречающихся кристаллических решеток. (ГЦК, ОЦК, кубическая).
Общие сведения по теме
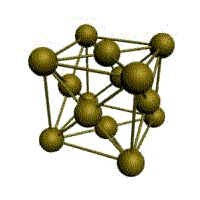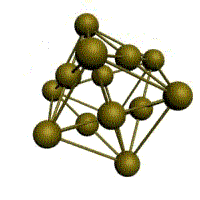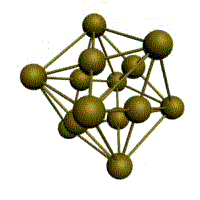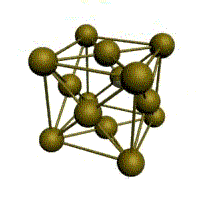
Гранецентрированная кубическая решетка
Атомы расположены в центрах граней и вершинах кубов, плотно заполняющих пространство. Соответствует одной из возможных плотных упаковок шаров в пространстве. Этой решеткой обладает ряд металлов(алюминий, золото, медь, серебро, никель, платина и др.) ее образуют при конденсации инертные газы.
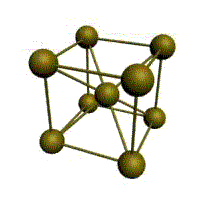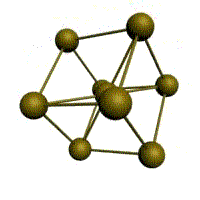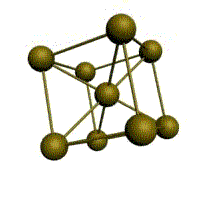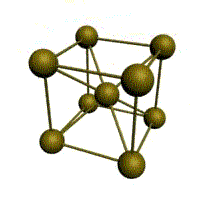
Объемно центрированная решётка
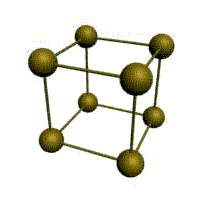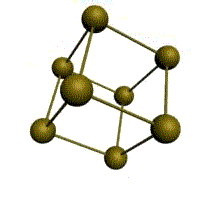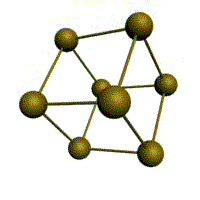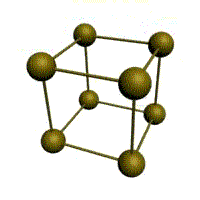
Основу ОЦК-решетки составляет элементарная кубическая ячейка (рис. 1.2,б), в которой положительно заряженные ионы металла находятся в вершинах куба, и еще один атом в центре его объема, т. е. на пересечении его диагоналей. Такой тип решетки в определенных диапазонах температур имеют железо, хром, ванадий, вольфрам, молибден и др. металлы.
Кубическая решетка
Простейший, но редко встречающийся тип решетки. Атомы расположены на вершинах куба.
Решение
Первый этап
Нахождение тензора жесткости второго порядка для плоской задачи, при равномерном радиальном расположении пружин одинаковой жесткости.
Результат: - общая формула, для нахождения тензора жесткости в этом случае, где Е -плоский единичный тензор 2-го ранга.
Второй этап
Нахождение тензора жесткости 2-го, 3-го и 4-го порядков для основных типов кристаллических решеток.(ОЦК, ГЦК, Кубическая)