Курсовые работы по ТОМДЧ: 2012-2013 — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
Строка 132: Строка 132:
  
 
<br style="clear: both" />
 
<br style="clear: both" />
 +
 +
 +
== Моделирование растяжения стержня квадратного сечения с концентратором напряжения ==
 +
 +
''' Исполнители ''' [[Клак Максим]]
 +
---
 +
 +
Рассматривается стержень квадратного сечения с канавкой, которая является концентратором напряжений. К торцевым граням стержня прикладывается продольная, растягивающая сила
 +
 +
[[Файл:Beam.gif]]
 +
 +
Для описания взаимодействия между частицами использовался потенциал Леонарда-Джонса.
 +
 +
<math>    U(r) = 4\varepsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^{6} \right], </math>
 +
 +
Радиус обрезания:
 +
 +
<math> r_{cut} = 1.3 </math>
 +
 +
Стержень состоит из 50 х 11 х 11 частиц, для расчета понадобилось ~ 1 000 - 1 400 шагов
 +
 +
В результате нагружения видно, что разрыв происходит в месте внедрения канавки (концентратора напряжений).
  
 
== См. также ==
 
== См. также ==

Версия 16:39, 25 января 2013

Общие сведения

Предмет: "Теоретические основы метода динамики частиц"

Лектор: Виталий Андреевич Кузькин

Группа: 40510

Учебный год: 2012-2013

Семестр: осень 2012

Моделирование кручения стержня квадратного сечения

Исполнители: Чебышев Игорь

Взаимодействие частиц:

[math]\varPi(r) [/math] - потенциал Леннарда-Джонса (парный силовой потенциал взаимодействия) и определяется формулой:

[math]\varPi(r) = D\left[\left(\frac{a}{r}\right)^{12}-2\left(\frac{a}{r}\right)^{6}\right][/math]

Сила взаимодействия определяется формулой:

[math]\vec{F}(\vec{r})= -\nabla\varPi(r) = \frac{12D}{a^2}\left[\left(\frac{a}{r}\right)^{14}-\left(\frac{a}{r}\right)^{8}\right]\vec{r}[/math]

Радиус обрезания:

[math]a_{cut}=1.3[/math]

Начальные условия:

[math]\vartheta = 0.001\vartheta_0[/math]

где

[math]\vartheta_0[/math] - скорость распространения длинных волн в среде.

Структура кристалла: ГЦК
Отношение сторон стержня:

[math]X/Y/Z = 8/1/1[/math]

Всего частиц:

[math]62500[/math]

Граничные условия:

Крайние сечения ( 2 ряда ) поворачиваем на угол [math]\alpha = 0,005/-0,005 [/math] радиан относительно оси симметрии, которая проходит вдоль стержня (Ось X)

Для поворота сечения используются следующие формулы:

[math]Y = y \cos(\alpha) - z \sin (\alpha)[/math]
[math]Z = y \sin (\alpha) + z \cos(\alpha)[/math]




Моделирование деформирования прямоугольной пластины под действием силы на группу частиц

‎

Исполнители: Цветков Денис

Рассматривается пластина, закрепленная сверху, под действием некоторой силы, действующей по оси х вдоль нижней грани пластины.

Для описания взаимодействия между частицами использовался потенциал Леннард-Джонса. На каждую частицу действует объемная сила, имитирующая гравитационные силы.

Пластина состоит из 15 х 40 х 4 частиц, для расчета понадобилось ~ 2000 шагов

Моделирование течения двухфазной жидкости

Исполнители: Буковская Карина

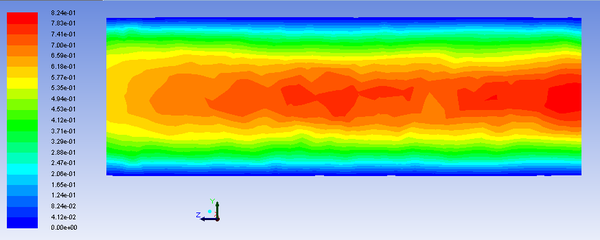
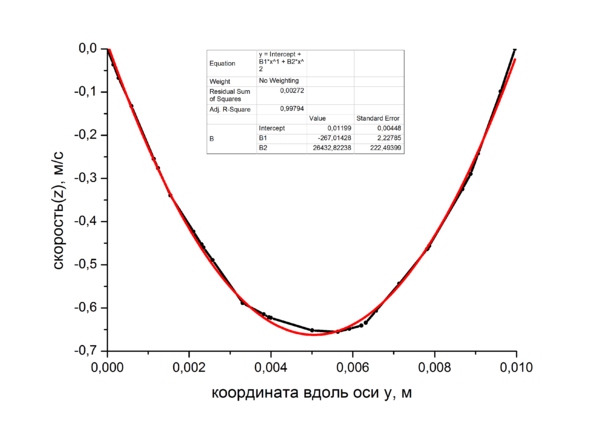
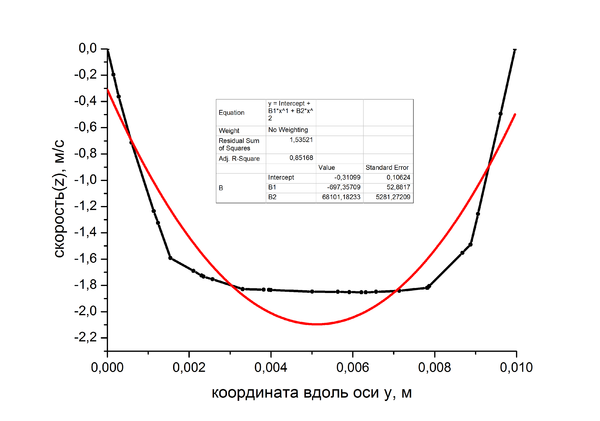
Одним из методов интенсификации работы нефтяных и газовых скважин является гидроразрыв пласта,который включает в себя создание трещины в целевом пласте для обеспечения притока нефти или газа к забою скважины.В данной работе проведено моделирование двухфазной жидкости (несущая жидкость и проппант) с использованием алгоритма совмещения пакетов ANSYS FLUENT и EDEM (Coupling Module). Целью является установление зависимости вязкости смеси от концентрации частиц проппанта. Для этого измеряются скорости модельной смеси при различных концентрациях твердой фазы и различных давлениях. Рассматривается установившееся течение несжимаемой жидкости с постоянной вязкостью в тонкой цилиндрической трубке круглого сечения под действием постоянной разности давлений. Если предположить, что течение будет ламинарным и одномерным, то уравнение решается аналитически, и для скорости получается параболический профиль (часто называемый профилем Пуазейля) — распределение скорости в зависимости от расстояния до оси канала 

                v=(ρ_1-ρ_1)/4μl(1-r^2)

v — скорость жидкости вдоль трубопровода, м/с;r — расстояние от оси трубопровода, м;p1 − p2 — разность давлений на входе и на выходе из трубы, Па;μ — вязкость жидкости, Н•с/м²;l — длина трубы, м. Закон Хагена — Пуазейля, определяющий расход жидкости при установившемся течении вязкой несжимаемой жидкости в тонкой цилиндрической трубе круглого сечения. 

               Q=(π∙d^4∙(ρ_(1-) ρ_2))/(128∙μ∙l)=(π∙r^4∙(ρ_(1-) ρ_2))/(8∙μ∙l)

Q — расход жидкости в трубопроводе, м³/с;d — диаметр трубопровода, м;r — радиус трубопровода, м;p1 − p2 — разность давлений на входе и на выходе из трубы, Па;μ — вязкость жидкости, Н•с/м²;l — длина трубы, м.

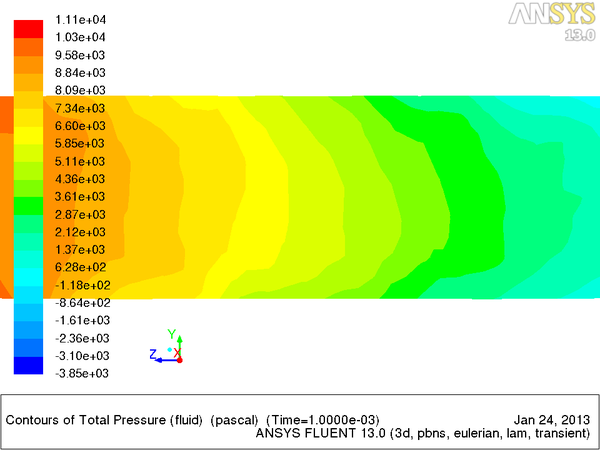
Расчет течения Пуазейля во FLUENT Рассматривается цилиндрическая трубка с диаметром основания 10мм ,длиной 30мм. В качестве жидкости было выбрано подобие воды с вязкостью в 20 раз больше воды (0.2 кг/(м*с)). Граничные условия:на входе давление 1000 Па,на выходе 0 Па. Сходимость решения достигалась за 70 итераций.


Vel.png

  • график показателей скорости

Pres.png

  • график показателей давления

Graf.png


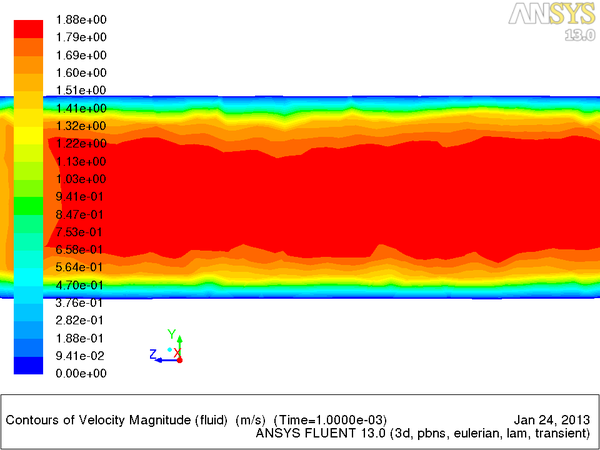
Расчет Coupling Module EDEM Была выбрана трубка тех же геометрических размеров,параметры жидкости неизменные.Граничные условия на входе скорость 1.5 м/с ,на выходе 0 Па. Количество частиц 5% от объема цилиндра (28125 частиц) размер : 1*10e-4, плотность 2500 кг/м^3. заданы периодические граничные условия. Добавление частиц привело к увеличению скорости потока предположительно из-за уменьшения общей вязкости потока.Построены профили распределения скоростей жидкости и смеси. Так же на представленных видео ,что распределение скоростей частиц по сечению соответствует распределению скоростей жидкости.

Velo pat.png

  • график показателей скорости с частицами

Pres pat.png

  • график показателей давления с частицами

Graph3.png



Моделирование продольного изгиба стержня. Потеря устойчивости под действием осевой силы

Исполнители: Дмитрий Ершов

рис. 1‎


В рассмотрении находится тонкий стержень, который покоится в начальный момент времени. На стержень начинает действовать постоянная продольная сжимающая сила P с разных концов стержня. Схема нагружения на рис.1. Необходимо проанализировать поведение стержня под действием сжимающей силы. Определить, при каком значении силы (критическая сила) будет происходить потеря устойчивости.

  • r=0.01‎

  • ‎r=0.005

  • r=0.003‎

  • r=0.001

  • r=0.0005‎

  • r=0.0001‎

Для описания взаимодействия между частицами использовался метод молекулярной динамики. Сила задается через перемещения концов стержня Стержень состоит из 800 частиц (400x2x2).

Рассмотрим перемещение противоположных концов с заданной скоростью. Ниже представлены разные формы потери устойчивости, зависящие от скорости перемещения противоположных концов стержня. Из моделирования видно, что при больших значениях скоростей происходит разрушение стержня, с уменьшением скорости наступает излом. Когда скорость мала, стержень приобретает криволинейную форму (синусоида).



Моделирование растяжения стержня квадратного сечения с концентратором напряжения

Исполнители Клак Максим ---

Рассматривается стержень квадратного сечения с канавкой, которая является концентратором напряжений. К торцевым граням стержня прикладывается продольная, растягивающая сила

Beam.gif

Для описания взаимодействия между частицами использовался потенциал Леонарда-Джонса.

[math] U(r) = 4\varepsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^{6} \right], [/math]

Радиус обрезания:

[math] r_{cut} = 1.3 [/math]

Стержень состоит из 50 х 11 х 11 частиц, для расчета понадобилось ~ 1 000 - 1 400 шагов

В результате нагружения видно, что разрыв происходит в месте внедрения канавки (концентратора напряжений).

См. также

Источник — «http://tm.spbstu.ru/?title=Курсовые_работы_по_ТОМДЧ:_2012-2013&oldid=16511»