Фролова Ксения. Курсовой проект по теоретической механике — различия между версиями
(→Решение) |
(→Решение) |
||
| (не показано 47 промежуточных версий этого же участника) | |||
| Строка 7: | Строка 7: | ||
* статические параметры: сила натяжения тетивы, величина рабочего хода<br> | * статические параметры: сила натяжения тетивы, величина рабочего хода<br> | ||
* динамические параметры: скорость распрямления дуг, амплитуда и длительность колебаний в дуге<br> | * динамические параметры: скорость распрямления дуг, амплитуда и длительность колебаний в дуге<br> | ||
| − | В рамках данной курсовой работы необходимо составить модель лука. Интересующей нас величиной является дальность полета стрелы. Задачей является выведение и последующее рассмотрение зависимости этой дальности от вышеуказанных параметров конструкции лука.<br> | + | В рамках данной курсовой работы необходимо составить модель прямого лука (плечи которого в состоянии без тетивы представляют собой палку). Интересующей нас величиной является дальность полета стрелы. Задачей является выведение и последующее рассмотрение зависимости этой дальности от вышеуказанных параметров конструкции лука.<br> |
'''Конкретизация:'''<br> | '''Конкретизация:'''<br> | ||
Стоит рассмотреть две модификации лука: в первом случае можно принять тетиву за нерастяжимую нить, а плечи за плоские пружины изгиба или же за стрержни, поместив пружину между ними; во втором случае стоит учитывать растяжимость тетивы. Далее необходимо рассчитать дальность полета стрелы.<br> | Стоит рассмотреть две модификации лука: в первом случае можно принять тетиву за нерастяжимую нить, а плечи за плоские пружины изгиба или же за стрержни, поместив пружину между ними; во втором случае стоит учитывать растяжимость тетивы. Далее необходимо рассчитать дальность полета стрелы.<br> | ||
| Строка 20: | Строка 20: | ||
Потенциальная энергия деформируемых плеч преобразуется не только в кинетическую энергию полета стрелы, но также и в ''кинетическую энергию тетивы, кинетическую энергию плеч, отдачу стрелку, колебания дуги, преодоление силы трения стрелы о "полочку".''<br> | Потенциальная энергия деформируемых плеч преобразуется не только в кинетическую энергию полета стрелы, но также и в ''кинетическую энергию тетивы, кинетическую энергию плеч, отдачу стрелку, колебания дуги, преодоление силы трения стрелы о "полочку".''<br> | ||
Так, необходимо ввести в рассмотрение КПД лука:<br> | Так, необходимо ввести в рассмотрение КПД лука:<br> | ||
| − | <math>\eta = \frac{T}{U}</math> | + | <math>\eta = \frac{T}{U}*100</math>%<br> |
Кинетическая энергия снаряда T:<br> | Кинетическая энергия снаряда T:<br> | ||
<math>T = \frac{mv_0^2}{2} </math><br> | <math>T = \frac{mv_0^2}{2} </math><br> | ||
Рассмотрим зависимость <math>\eta \sim m</math>:<br> | Рассмотрим зависимость <math>\eta \sim m</math>:<br> | ||
- если m очень мало, то выстрел "как бы холостой" <math>\Rightarrow \eta</math> мало;<br> | - если m очень мало, то выстрел "как бы холостой" <math>\Rightarrow \eta</math> мало;<br> | ||
| − | - если m слишком велико, то уменьшается ускорение, сообщаемое стреле, увеличивается отдача лука, увеличивается сила трения <math>\Rightarrow T \searrow \Rightarrow \eta \searrow</math><br> | + | - если m слишком велико, то уменьшается ускорение, сообщаемое стреле, увеличивается отдача лука, увеличивается сила трения <math>\Rightarrow \quad T \searrow \quad \Rightarrow \quad \eta \searrow</math><br> |
Таким образом, нужно искать баланс. Опыты показывают, что КПД составляет 30% - 85%<br> | Таким образом, нужно искать баланс. Опыты показывают, что КПД составляет 30% - 85%<br> | ||
Начальная скорость стрелы обратно пропорциональна времени, а время, в течение которого накапливается потенциальная энергия для последующего перехода в кинетическую зависит от величины рабочего хода (или же просто от смещения тетивы, если лук натягивается не до "упора"), а также от массы стрелы. В современных луках начальная скорость составляет 40 - 80 м/с.<br> | Начальная скорость стрелы обратно пропорциональна времени, а время, в течение которого накапливается потенциальная энергия для последующего перехода в кинетическую зависит от величины рабочего хода (или же просто от смещения тетивы, если лук натягивается не до "упора"), а также от массы стрелы. В современных луках начальная скорость составляет 40 - 80 м/с.<br> | ||
'''Мощность лука'''<br> | '''Мощность лука'''<br> | ||
| − | <math>P = \frac{U}{t} | + | <math>P \ =\ \frac{U}{t} \quad P \sim \frac{1}{t},\quad \frac{1}{m}</math><br> |
| − | Так, для того, чтобы <math>P \searrow</math>, необходимо, чтобы <math>t \searrow, m \searrow</math><br> | + | Так, для того, чтобы <math>P \searrow</math>, необходимо, чтобы <math>t \searrow,\quad m \searrow</math><br> |
| − | Для того, чтобы <math>v_0 \ | + | Для того, чтобы <math>v_0 \nearrow </math>, необходимо, чтобы <math>t \searrow \quad \Rightarrow \quad l \searrow,\quad m \searrow</math>, но при этом масса стрелы не должна быть слишком мала. Опыты показывают, что ее величина должна составлять 15 - 40 г<br> |
'''Баллистика'''<br> | '''Баллистика'''<br> | ||
Наглядное сравнение стрельбы из огнестрельного оружия и стрельбы из лука. Дело в том, что в огнестрельном оружии не учитывается баллистика, в отличие от лука и арбалета.<br> | Наглядное сравнение стрельбы из огнестрельного оружия и стрельбы из лука. Дело в том, что в огнестрельном оружии не учитывается баллистика, в отличие от лука и арбалета.<br> | ||
Рассмотрим прямой выстрел(начальная скорость направлена параллельно земле):<br> | Рассмотрим прямой выстрел(начальная скорость направлена параллельно земле):<br> | ||
| − | Пусть известны следующие величины: <math>v_0 = 800</math>м/с - скорость пули, <math>v_1 = 80</math>м/с - скорость стрелы, расстояние s = 200 м<br> | + | Пусть известны следующие величины: <math>v_0 = 800\quad </math> м/с - скорость пули, <math>v_1 = 80 \quad </math> м/с - скорость стрелы, расстояние s = 200 м<br> |
| − | Время полета пули:<math>t = \frac{200}{800} = \frac{1}{4}</math> с, время полета стрелы: <math>t = \frac{200}{80} = \frac{5}{2}</math> с<br> | + | Время полета пули:<math>t =\frac{200}{800} = \frac{1}{4}\quad </math> с, время полета стрелы: <math>t = \frac{200}{80} = \frac{5}{2}\quad </math> с<br> |
| − | <math>h = \frac{gt^2}{2} </math>, высота, на которую пуля окажется ниже мишени, составит <math>h = \frac{10}{32} = 0.3125</math>м<br> | + | <math>h = \frac{gt^2}{2} </math>, высота, на которую пуля окажется ниже мишени, составит <math>h = \frac{10}{32} = 0.3125\quad </math> м<br> |
Таким образом, если брать в расчет высоту снайпера, то пуля не "войдет в землю" и, в зависимости от масштабов мишени, может попасть в нее.<br> | Таким образом, если брать в расчет высоту снайпера, то пуля не "войдет в землю" и, в зависимости от масштабов мишени, может попасть в нее.<br> | ||
| − | Высота же, на которую стрела окажется ниже мишени составит: <math>h = \frac{250}{82} = 31.25</math>м, откуда сразу же видно, что, учитывая высоту стрелка, пуля войдет в землю и не достигнет мишени.<br> | + | Высота же, на которую стрела окажется ниже мишени составит: <math>h = \frac{250}{82} = 31.25\quad </math> м, откуда сразу же видно, что, учитывая высоту стрелка, пуля войдет в землю и не достигнет мишени.<br> |
'''Факторы стрельбы''' | '''Факторы стрельбы''' | ||
| − | *дальность стрельбы (450 м | + | *дальность стрельбы (450 м - рекорд для спортивных луков);<br> |
| − | *дальность поражения (60 - 80 м для поражения защищенного доспехами человека, 250 | + | *дальность поражения (60 - 80 м для поражения защищенного доспехами человека, 180 - 250 м для незащищенного человека)<br> |
Существует эффективная прицельная дальность стрельбы - дистанция, на которой возможно гарантированное попадание стрелы в реальную подвижную цель, не успевающую выйти из зоны поражения. Эта величина составляет примерно 30 - 40 м)<br> | Существует эффективная прицельная дальность стрельбы - дистанция, на которой возможно гарантированное попадание стрелы в реальную подвижную цель, не успевающую выйти из зоны поражения. Эта величина составляет примерно 30 - 40 м)<br> | ||
'''Поправки'''<br> | '''Поправки'''<br> | ||
| Строка 50: | Строка 50: | ||
Пусть скорость ветра <math>v_0 \approx 1</math> м/с, скорость стрелы <math>v_1 \approx 80</math> м/с, пусть скорость ветра перпендикулярна начальной скорости стрелы<br> | Пусть скорость ветра <math>v_0 \approx 1</math> м/с, скорость стрелы <math>v_1 \approx 80</math> м/с, пусть скорость ветра перпендикулярна начальной скорости стрелы<br> | ||
Рассмотрим дистанцию в 40 м<br> | Рассмотрим дистанцию в 40 м<br> | ||
| − | + | <math>\tan\alpha = \frac{1}{80} = \frac{h}{40} \quad \Rightarrow\quad h = \frac{40}{80} = 0.5 </math>, где h - смещение<br> | |
== Решение == | == Решение == | ||
| + | '''Рассмотрим следующую модификацию лука:плечи приняты за стрежни, между ними находится пружина, тетива рассматривается как нерастяжимая нить'''<br> | ||
'''От каких параметров зависит силовая характеристика лука?'''<br> | '''От каких параметров зависит силовая характеристика лука?'''<br> | ||
| − | <math>M = \gamma*\varphi\triangle</math><br> | + | <math>M \ =\ \gamma*\triangle\varphi</math>, где M - момент пружины, действующий на плечо лука, <math>\frac{\triangle\varphi}{2}</math> - угол смещения плеча от начального положения при натяжении тетивы. В силу симметрии картины изгиба плеч лука в уравнение для момента входит величина угла изгиба плеча, умноженная на 2.<br> |
| − | <math>T*h = M = \gamma*\triangle\varphi</math><br> | + | <math>T*h \ =\ M =\ \gamma*\triangle\varphi</math>, где T - сила упругости тетивы, h - плечо силы T.<br> |
| − | <math>T = \gamma*\frac{\triangle\varphi}{h}</math><br> | + | <math>T \ =\ \gamma*\frac{\triangle\varphi}{h}</math><br> |
| − | <math>F = 2*T*\cos\beta | + | <math>F \ =\ 2*T*\cos\beta \ =\ 2*\gamma*\frac{\triangle\varphi}{h}*\cos\beta</math>, F - сила, приложенная к тетиве и затем передающаяся стреле при спускании тетивы<br> |
'''Геометрия'''<br> | '''Геометрия'''<br> | ||
| − | *Найдем <math>\angle\beta</math>, а точнее <math>\cos\beta</math>:<br> | + | <gallery widths=150px heights=150px perrow = 1> |
| − | По обобщенной теореме косинусов и при последующем упрощении получается, что <math>\cos\beta = \frac{\triangle x^2 + 2\triangle xx_0}{2\sqrt{l^2 - x_0^2}*(\triangle x + x_0)}</math><br> | + | Файл:Ang.1.bmp |
| + | </gallery> | ||
| + | |||
| + | *Найдем <math>\angle\beta</math>, а точнее, <math>\cos\beta</math>:<br> | ||
| + | По обобщенной теореме косинусов и при последующем упрощении получается, что <math>\cos\beta \ =\ \frac{\triangle x^2 + 2\triangle xx_0}{2\sqrt{l^2 - x_0^2}*(\triangle x + x_0)}</math><br> | ||
*Найдем h - плечо силы натяжения тетивы:<br> | *Найдем h - плечо силы натяжения тетивы:<br> | ||
| − | <math>h = (\triangle x + x_0)\sin\beta \Rightarrow h = \frac{\sqrt{4(l^2 - x_0^2)^2*(\triangle x + x_0)^2 - (\triangle x^2 + 2\triangle xx_0)^2}}{2\sqrt{l^2 - x_0^2}}</math><br> | + | <math>h \ =\ (\triangle x + x_0)\sin\beta \quad \Rightarrow \quad h \ =\ \frac{\sqrt{4(l^2 - x_0^2)^2*(\triangle x + x_0)^2 - (\triangle x^2 + 2\triangle xx_0)^2}}{2\sqrt{l^2 - x_0^2}}</math><br> |
*Найдем <math>\triangle \varphi</math>:<br> | *Найдем <math>\triangle \varphi</math>:<br> | ||
| − | <math>\varphi = \chi - \gamma = 2*(\arcsin(\frac{\sqrt{l^2 - x_0^2}}{l^2}*(\sqrt{l^2 - (l^2 - x_0^2)\sin\beta^2}) -\sin\beta*x_0)))</math><br> | + | <gallery widths=150px heights=150px perrow = 1> |
| + | Файл:Ang2.PNG | ||
| + | </gallery> | ||
| + | <math>\varphi \ =\ \chi - \gamma \ =\ 2*(\arcsin(\frac{\sqrt{l^2 - x_0^2}}{l^2}*(\sqrt{l^2 - (l^2 - x_0^2)\sin\beta^2}) -\sin\beta*x_0)))</math><br> | ||
*Найдем <math>\frac{\triangle\varphi}{h}*\cos\beta</math>:<br> | *Найдем <math>\frac{\triangle\varphi}{h}*\cos\beta</math>:<br> | ||
| − | <math>\frac{\triangle\varphi}{h}*\cos\beta = \frac{\triangle x^2 + 2\triangle xx_0}{(\triangle x + x_0)\sqrt{4(l^2 - x_0^2)(\triangle x + x_0)^2 - (\triangle x + 2\triangle xx_0)^2}}*2\arcsin(\frac{\sqrt{l^2 - x_0^2}}{l^2}*(\sqrt{l^2 - (l^2 - x_0^2)\sin\beta^2}) -\sin\beta*x_0))</math><br> | + | <math>\frac{\triangle\varphi}{h}*\cos\beta \ =\ \frac{\triangle x^2 + 2\triangle xx_0}{(\triangle x + x_0)\sqrt{4(l^2 - x_0^2)(\triangle x + x_0)^2 - (\triangle x + 2\triangle xx_0)^2}}*2\arcsin(\frac{\sqrt{l^2 - x_0^2}}{l^2}*(\sqrt{l^2 - (l^2 - x_0^2)\sin\beta^2}) -\sin\beta*x_0))</math><br> |
'''Нахождение силовой характеристики лука'''<br> | '''Нахождение силовой характеристики лука'''<br> | ||
| − | <math>F = F(\triangle x) = \frac{\partial F}{\partial 0}(0)\triangle x+ \frac{1}{2}*\frac{\partial^2F}{\partial \triangle x^2}(0)(\triangle x)^2 + \frac{1}{6}*\frac{\partial^3F}{\partial \triangle x^3}(0)(\triangle x)^3</math><br> | + | <math>F = F(\triangle x) \ =\ \frac{\partial F}{\partial 0}(0)\triangle x+ \frac{1}{2}*\frac{\partial^2F}{\partial \triangle x^2}(0)(\triangle x)^2 + \frac{1}{6}*\frac{\partial^3F}{\partial \triangle x^3}(0)(\triangle x)^3</math><br> |
Проведенные расчеты показали, что | Проведенные расчеты показали, что | ||
| − | <math>\frac{\partial F}{\partial 0}(0) = 0 ;\frac{\partial^2F}{\partial \triangle x^2}(0) = 0</math><br> | + | <math>\frac{\partial F}{\partial 0}(0) \ =\ 0 ;\quad \frac{\partial^2F}{\partial \triangle x^2}(0) \ =\ 0</math><br> |
| − | <math>\frac{\partial^3F}{\partial \triangle x^3}(0) = \frac{12\gamma(l^2 - 2x_0^2)}{l^2x_0^2\sqrt{(l^2 - x_0^2)}} </math><br> | + | <math>\frac{\partial^3F}{\partial \triangle x^3}(0) \ =\ \frac{12\gamma(l^2 - 2x_0^2)}{l^2x_0^2\sqrt{(l^2 - x_0^2)}} </math><br> |
| − | Таким образом, <math>F(\triangle x) = \ | + | Таким образом, <math>F(\triangle x) \ =\ \frac{2\gamma(l^2 - 2x_0^2)}{l^2x_0^2(l^2 - x_0^2)}*\triangle x^3</math><br> |
'''Решение задачи на непосредственно нахождение дальности полета стрелы'''<br> | '''Решение задачи на непосредственно нахождение дальности полета стрелы'''<br> | ||
''Весь процесс стрельбы из лука можно разделить на два этапа: натяжение тетивы и полет выпущенной стрелы. Для нахождения интересующей нас дальности полета стрелы необходимо знать начальную скорость, с которой выпущена стрела. Для нахождения же этой скорости необходимо рассматривать процесс натяжения тетивы. Итак, рассмотрим два этапа.''<br> | ''Весь процесс стрельбы из лука можно разделить на два этапа: натяжение тетивы и полет выпущенной стрелы. Для нахождения интересующей нас дальности полета стрелы необходимо знать начальную скорость, с которой выпущена стрела. Для нахождения же этой скорости необходимо рассматривать процесс натяжения тетивы. Итак, рассмотрим два этапа.''<br> | ||
*Этап натяжения тетивы<br> | *Этап натяжения тетивы<br> | ||
| − | По второму закону Ньютона <math>F = mw</math><br> | + | По второму закону Ньютона <math>F\ =\ mw</math><br> |
| − | С другой стороны сила равна найденной величине: <math>F(\triangle x) = \frac{2\gamma(l^2 - 2x_0^2)}{l^2x_0^2\sqrt{(l^2 - x_0^2)}*\triangle x^3 | + | С другой стороны, сила равна найденной величине: <math>F(\triangle x) \ =\ \frac{2\gamma(l^2 - 2x_0^2)}{l^2x_0^2\sqrt{(l^2 - x_0^2)}}*\triangle x^3</math><br> |
Отсюда можно найти ускорение, переданное стреле:<br> | Отсюда можно найти ускорение, переданное стреле:<br> | ||
| − | <math>w = \frac{2\gamma(l^2 - 2x_0^2)}{ml^2x_0^2\sqrt{(l^2 - x_0^2)}*\triangle x^3}</math><br> | + | <math>w \ =\ \frac{2\gamma(l^2 - 2x_0^2)}{ml^2x_0^2\sqrt{(l^2 - x_0^2)}*\triangle x^3}</math><br> |
| − | <math>\triangle x = \frac{1}{2}wt^2 + x_0 \Rightarrow w = \frac{2\gamma(l^2 - 2x_0^2)}{ml^2x_0^2\sqrt{(l^2 - x_0^2)}*\triangle x^3}*(\frac{1}{8}w^3t^6 + x_0^3)</math><br> | + | <math>\triangle x \ =\ \frac{1}{2}wt^2 + x_0 \quad \Rightarrow \quad w \ =\ \frac{2\gamma(l^2 - 2x_0^2)}{ml^2x_0^2\sqrt{(l^2 - x_0^2)}*\triangle x^3}*(\frac{1}{8}w^3t^6 + x_0^3)</math><br> |
| − | <math>v_0 = wt = | + | <math>v_0 \ =\ wt \ =\ \frac{2\gamma(l^2 - 2x_0^2)}{ml^2x_0^2\sqrt{(l^2 - x_0^2)}*\triangle x^3}*(\frac{1}{8}w^3t^6 + x_0^3)*t</math><br> |
Выразим одну неизвестную величину через другую (ускорение через время). В луке величину квадрата начального смещения, а также куб этой величины можно cчитать малой в сравнении со степенями величины длины плеча лука.<br> | Выразим одну неизвестную величину через другую (ускорение через время). В луке величину квадрата начального смещения, а также куб этой величины можно cчитать малой в сравнении со степенями величины длины плеча лука.<br> | ||
| − | <math>w = \frac{2lx_0\sqrt{m}}{t^3\sqrt{\gamma}}</math><br> | + | <math>w \ =\ \frac{2lx_0\sqrt{m}}{t^3\sqrt{\gamma}}</math><br> |
Тогда | Тогда | ||
| − | <math>v_0 = \frac{2\sqrt{m}lx_0}{t^2\sqrt{\gamma}}</math><br> | + | <math>v_0 \ =\ \frac{2\sqrt{m}lx_0}{t^2\sqrt{\gamma}}</math><br> |
| − | <math>t = \frac{lx_0\sqrt{m}}{ | + | <math>t \ =\ \frac{lx_0\sqrt{m}}{\triangle x \sqrt{\gamma}}</math><br> |
Тогда | Тогда | ||
| − | <math>v_0 = \frac{2\sqrt{\gamma} | + | <math>v_0 \ =\ \frac{2\sqrt{\gamma}\triangle x^2}{lx_0\sqrt{m}}</math><br> |
*Этап полета стрелы<br> | *Этап полета стрелы<br> | ||
| − | <math>s = v_0\cos\alpha*t</math><br> | + | <math>s \ =\ v_0\cos\alpha*t</math><br> |
Найдем время полета стрелы.<br> | Найдем время полета стрелы.<br> | ||
| − | <math>g = \frac{v_0\sin\alpha}{t/2} \Rightarrow t = \frac{ | + | <math>g \ =\ \frac{v_0\sin\alpha}{t/2} \quad \Rightarrow \quad t \ =\ \frac{4\sqrt{\gamma}\triangle x^2\sin\alpha}{lx_0\sqrt{m}g}</math><br> |
| − | <math>s = v_0\cos\alpha\frac{ | + | <math>s \ =\ v_0\cos\alpha\frac{4\sqrt{\gamma}\triangle x^2\sin\alpha}{lx_0\sqrt{m}g} \ =\ \frac{4\gamma\triangle x^4\sin2\alpha}{l^2x_0^2mg}</math><br> |
| + | '''Рассмотрим модификацию лука, когда тетива принимается за растяжимую нить'''<br> | ||
| + | Если принимать тетиву за растяжимую нить, то при смещении тетивы и накоплении потенциальной энергии <math>\angle\beta</math> будет отличен от вычисленного для нерастяжимой нити. Также изменится угол отклонения плеч от положения, рассматриваемого в качестве начального - когда тетива натянула на лук и не деформирована стрелком. В следствие изменения <math>\angle\beta</math> изменится и плечо силы натяжения тетивы. Так, изменится вся величина силы.<br> | ||
| + | Сила натяжения нити: <math>T \ =\ c*\triangle p \ =\ c*(p - p_0)</math>, где величина p - длина тетивы в натянутом состоянии, а <math>p_0</math> - длина тетивы в положении, рассматриваемом в качестве начального<br> | ||
| + | Для вычисления длины нити в промежуточный момент времени мы введем систему из трех уравнений. Первое уравнение заключается в обобщенной теореме Пифагора,второе уравнение получается из рассмотрения статического равновесия в середине тетивы (месте приложения силы, действующей на стрелу), а третье из рассмотрения положения статического равновесия системы тетива - плечо лука в некоторый момент времени.<br> | ||
| + | Итак, <math>p^2 \ =\ (\triangle x + x_0)^2 + l^2 - 2*(\triangle x + x_0)l\cos(\chi - \frac{\triangle\varphi}{2})\quad</math><br> | ||
| + | <math>M \ =\ Th \quad \Rightarrow \quad \gamma\triangle\varphi \ =\ c(p - \sqrt{l^2 - x_0^2})*h</math><br> | ||
| + | Так, <math>p^2 \ =\ \frac{(\gamma\triangle\varphi)^2}{c^2} + (\triangle x + x_0) - l\cos(\chi - \frac{\triangle\varphi}{2})</math><br> | ||
| + | <math>F \ \ = 2T\cos\beta \ =\ 2c(p - \sqrt{l^2 - x_0^2}\cos\beta)</math>, с другой стороны, <math>F \ =\ 2\gamma\frac{\triangle\varphi}{h}*\cos\beta</math><br> | ||
| + | Так, получаем, что <math>c \ =\ \frac{\gamma\triangle\varphi}{h(p - \sqrt{l^2 - x_0^2}}</math><br> | ||
| + | Решение системы получается весьма нетривиальным, а потому можно прибегнуть к упрощению полученного уравнения для величины угла смещения плеч. Упрощение происходит посредством отбрасывания малых величин.<br> | ||
| + | Уравнение для силы, действующей на стрелу, выглядит следующим образом:<math>F \ =\ 4\gamma*\arccos(\frac{\sqrt{l^2 - x_0^2}}{l}*\sqrt{1 + \frac{l}{2(\triangle x + x_0)}})*\frac{\sqrt{4(\triangle x + x_0)^2 + l^2}}{l(\triangle x + x_0)})</math><br> | ||
| + | '''Случай малых углов'''<br> | ||
| + | Рассмотрим случай, когда смещение тетивы от положения равновесия мало, то есть <math>\angle\kappa</math> и <math>\angle \xi</math> малы.<br> | ||
| + | |||
| + | <gallery widths=150px heights=150px perrow = 1> | ||
| + | Файл:Ang_new.bmp | ||
| + | </gallery> | ||
| + | |||
| + | Выразим величину <math>\triangle x</math> через малые углы.<br> | ||
| + | <math>\triangle x + x_0 \ =\ p\sin\kappa + l\sin\xi</math><br> | ||
| + | Выразим малые углы через известные:<br> | ||
| + | <math>\angle\kappa \ =\ \frac{\pi}{2} - \beta</math><br> | ||
| + | <math>\angle\xi \ =\ \frac{\pi}{2} - \arcsin(\frac{p}{l}\sin\beta)</math><br> | ||
| + | Итак, <math>\triangle x \ =\ \frac{\pi}{2}(l - p) - x_0</math><br> | ||
| + | Сила, прикладываемая к середине тетивы, в таком случае выражается следующим образом:<br> | ||
| + | <math>F \ =\ \frac{2\gamma(l^2 - 2x_0^2)}{l^2x_0^2(l^2 - x_0^2)}*(\frac{\pi}{2}(l - \sqrt{l^2 - x_0^2})- x_0)^3</math><br> | ||
| + | Дальность же полета окажется равной:<br> | ||
| + | <math>s \ =\ \frac{4\gamma\triangle x^4\sin2\alpha}{l^2x_0^2mg}\ =\ \frac{4\gamma(\frac{\pi}{2}(l - \sqrt{l^2 - x_0^2}) - x_0)^4\sin2\alpha}{l^2x_0^2mg}</math><br> | ||
| + | |||
| + | '''Небольшое исследование зависимостей в полученной модели'''<br> | ||
| + | <math>P \ =\ \frac{U}{t}</math><br> | ||
| + | Интегрирование полученного выражения для силы натяжения тетивы по смещению даст следующее выражение для мощности:<br> | ||
| + | <math>P \ =\ v_0*\frac{F}{4}</math><br> | ||
| + | Поскольку <math>U \ =\ \frac{F*\triangle x}{4}</math>, получаем, что<br> | ||
| + | <math>v_0 \ =\ \frac{\triangle x}{t}</math><br> | ||
| + | <math>m \ =\ \eta *\frac{2U}{v_0^2}</math><br> | ||
| + | <math>m \ =\ \eta*\frac{F*\triangle x}{2*v_0^2}</math><br> | ||
| + | <math>m \ = \eta*\frac{F*t^2}{2*\triangle x}</math><br> | ||
| + | |||
| + | '''Нахождение изгибающего момента в сечении плеча лука'''<br> | ||
| + | <math>M \ =\ EI(K - K_0)</math><br> | ||
| + | <math>K \ =\ \frac{y^{\prime\prime}}{\sqrt{((1 + (y^\prime)^2)^3)}}</math><br> | ||
| + | <math>K \ =\ \frac{1}{r} \ =\ ms</math><br> | ||
| + | <math>y^\prime \ =\ \sqrt{\frac{m^2*(\frac{s^2 + 2c_1}{2})^2}{1 - m^2*(\frac{s^2 + 2c_1}{2})^2 }}</math><br> | ||
== Обсуждение результатов и выводы == | == Обсуждение результатов и выводы == | ||
| + | Одним из основных вопросов, влияющих на вычисления, было выявление характера зависимости прикладываемой к тетиве силы от смещения тетивы. Из ранее проведенного опыта (''Искусство стрельбы из лука. Фролова Ксения.(скачать презентацию: ppt,[[Медиа:Prsl.ppt| 1.09 MB]])'') можно наглядно увидеть динамическую кривую (изображение данной характеристики на графике) простого прямого лука (ролевого с текстолитовыми плечами), имеющегося в наличии, а также из проделанной работы по классификации различных модификаций обсуждаемого метательного оружия можно выделить для рассмотрения динамические кривые опять же прямого прямого лука, рекурсивного лука и современного блочного лука. Вычисления в рамках данной курсовой работы велись для наиболее простой модели лука - прямого лука, плечи которого в состоянии без тетивы представляют собой прямую палку. Полученная зависимость оказалось отнюдь нелинейной. Оказалось, что прикладываемая к тетиве сила зависит от куба величины смещения тетивы, от квадрата величины длины плеча лука, от квадрата величины начального смещения тетивы (когда тетива одета на лук, к которому не прикладывается сила), от жесткости материала, из которого сделаны плечи лука.<br> | ||
| + | Также в качестве исследования нужно было рассмотреть тетиву как нерастяжимую нить и как растяжимую, выяснив, что более влияет на полет стрелы при спуске - сила упругости плеч или же тетивы лука. Полученные результаты показали, что величина силы, действующей на стрелу при спуске различна для этих случаев. В следствие этого можно сделать вывод, что пренебрегать удлинением нити не следует.<br> | ||
| + | Используя полученную модель лука, мы четко видим поведение стрелы в предельных случаях. При стрельбе из лука в горизонтальном направлении мы получаем нулевую дальность, равно, как и при вертикальной стрельбе. Реально же дальность полета снаряда зависит от высоты человека (расстояния от земли до уровня середины тетивы, в месте которой прикладывается сила). Также из полученной модели видно, что при малых углах (малом оттягивании тетивы от положения равновесия), дальность полета - малая величина. При обращении же величины смещения тетивы в ноль, дальность полета оказывается также равной нулю, то есть, полета стрелы не будет.<br> | ||
| − | == Ссылки по теме == | + | == Ссылки по теме == |
| + | *Искусство стрельбы из лука. Фролова Ксения.(скачать презентацию: ppt,[[Медиа:Prsl.ppt| 1.09 MB]]) | ||
| + | *[http://www.dial-engineering.ru/0ftp/files/Energy&mass-2.pdf Энергия метательного снаряда] | ||
| + | *[http://engineerd.narod.ru/ Луки и стрелы, современные и древние] | ||
== См. также == | == См. также == | ||
Текущая версия на 20:06, 7 декабря 2012
Содержание
Тема проекта[править]
Моделирование стрельбы из лука
Модель лука
Постановка задачи[править]
Существуют статические и динамические параметры конструкции лука.
- статические параметры: сила натяжения тетивы, величина рабочего хода
- динамические параметры: скорость распрямления дуг, амплитуда и длительность колебаний в дуге
В рамках данной курсовой работы необходимо составить модель прямого лука (плечи которого в состоянии без тетивы представляют собой палку). Интересующей нас величиной является дальность полета стрелы. Задачей является выведение и последующее рассмотрение зависимости этой дальности от вышеуказанных параметров конструкции лука.
Конкретизация:
Стоит рассмотреть две модификации лука: в первом случае можно принять тетиву за нерастяжимую нить, а плечи за плоские пружины изгиба или же за стрержни, поместив пружину между ними; во втором случае стоит учитывать растяжимость тетивы. Далее необходимо рассчитать дальность полета стрелы.
Краткий экскурс[править]
Общий принцип
Причиной движения стрелы является переход потенциальной энергии деформируемого тела в кинетическую энергию полета снаряда. Реализация происходит посредством сравнительно медленного оттягивания тетивы, в течение которого накапливается потенциальная энергия упругости плеч лука, последующего спуска тетивы, когда плечи, разгибаясь, преобразуют накопленную энергию в кинетическую энергию полета стрелы, а также непосредственно полета стрелы, происходящего за счет полученной кинетической энергии.
Преобразование потенциальной энергии деформируемого тела в кинетическую энергию полета стрелы
Одним из основных боевых качеств лука является его силовая характеристика - зависимость силы натяжения, прикладываемой к тетиве, от смещения тетивы из положения равновесия. Изображая данную зависимость на графике, мы получаем динамическую кривую.
Пусть силовая характеристика известна (эту зависимость нетрудно получить экспериментальным путем, оттягивая тетиву на горизонтально покоящемся луке с помощью гирек разных масс). Тогда мы можем вычислить потенциальную энергию, накапливаемую за счет оттягивания тетивы путем взятия интеграла:
, где является величиной рабочего хода (максимальной величиной смещения тетивы)
Потенциальная энергия деформируемых плеч преобразуется не только в кинетическую энергию полета стрелы, но также и в кинетическую энергию тетивы, кинетическую энергию плеч, отдачу стрелку, колебания дуги, преодоление силы трения стрелы о "полочку".
Так, необходимо ввести в рассмотрение КПД лука:
%
Кинетическая энергия снаряда T:
Рассмотрим зависимость :
- если m очень мало, то выстрел "как бы холостой" мало;
- если m слишком велико, то уменьшается ускорение, сообщаемое стреле, увеличивается отдача лука, увеличивается сила трения
Таким образом, нужно искать баланс. Опыты показывают, что КПД составляет 30% - 85%
Начальная скорость стрелы обратно пропорциональна времени, а время, в течение которого накапливается потенциальная энергия для последующего перехода в кинетическую зависит от величины рабочего хода (или же просто от смещения тетивы, если лук натягивается не до "упора"), а также от массы стрелы. В современных луках начальная скорость составляет 40 - 80 м/с.
Мощность лука
Так, для того, чтобы , необходимо, чтобы
Для того, чтобы , необходимо, чтобы , но при этом масса стрелы не должна быть слишком мала. Опыты показывают, что ее величина должна составлять 15 - 40 г
Баллистика
Наглядное сравнение стрельбы из огнестрельного оружия и стрельбы из лука. Дело в том, что в огнестрельном оружии не учитывается баллистика, в отличие от лука и арбалета.
Рассмотрим прямой выстрел(начальная скорость направлена параллельно земле):
Пусть известны следующие величины: м/с - скорость пули, м/с - скорость стрелы, расстояние s = 200 м
Время полета пули: с, время полета стрелы: с
, высота, на которую пуля окажется ниже мишени, составит м
Таким образом, если брать в расчет высоту снайпера, то пуля не "войдет в землю" и, в зависимости от масштабов мишени, может попасть в нее.
Высота же, на которую стрела окажется ниже мишени составит: м, откуда сразу же видно, что, учитывая высоту стрелка, пуля войдет в землю и не достигнет мишени.
Факторы стрельбы
- дальность стрельбы (450 м - рекорд для спортивных луков);
- дальность поражения (60 - 80 м для поражения защищенного доспехами человека, 180 - 250 м для незащищенного человека)
Существует эффективная прицельная дальность стрельбы - дистанция, на которой возможно гарантированное попадание стрелы в реальную подвижную цель, не успевающую выйти из зоны поражения. Эта величина составляет примерно 30 - 40 м)
Поправки
- ветер;
- подвижная цель;
Наглядное представление:
Пусть скорость ветра м/с, скорость стрелы м/с, пусть скорость ветра перпендикулярна начальной скорости стрелы
Рассмотрим дистанцию в 40 м
, где h - смещение
Решение[править]
Рассмотрим следующую модификацию лука:плечи приняты за стрежни, между ними находится пружина, тетива рассматривается как нерастяжимая нить
От каких параметров зависит силовая характеристика лука?
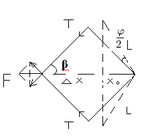
, где M - момент пружины, действующий на плечо лука, - угол смещения плеча от начального положения при натяжении тетивы. В силу симметрии картины изгиба плеч лука в уравнение для момента входит величина угла изгиба плеча, умноженная на 2.
, где T - сила упругости тетивы, h - плечо силы T.
, F - сила, приложенная к тетиве и затем передающаяся стреле при спускании тетивы
Геометрия
- Найдем , а точнее, :
По обобщенной теореме косинусов и при последующем упрощении получается, что
- Найдем h - плечо силы натяжения тетивы:
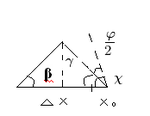
- Найдем :
- Найдем :
Нахождение силовой характеристики лука
Проведенные расчеты показали, что
Таким образом,
Решение задачи на непосредственно нахождение дальности полета стрелы
Весь процесс стрельбы из лука можно разделить на два этапа: натяжение тетивы и полет выпущенной стрелы. Для нахождения интересующей нас дальности полета стрелы необходимо знать начальную скорость, с которой выпущена стрела. Для нахождения же этой скорости необходимо рассматривать процесс натяжения тетивы. Итак, рассмотрим два этапа.
- Этап натяжения тетивы
По второму закону Ньютона
С другой стороны, сила равна найденной величине:
Отсюда можно найти ускорение, переданное стреле:
Выразим одну неизвестную величину через другую (ускорение через время). В луке величину квадрата начального смещения, а также куб этой величины можно cчитать малой в сравнении со степенями величины длины плеча лука.
Тогда
Тогда
- Этап полета стрелы
Найдем время полета стрелы.
Рассмотрим модификацию лука, когда тетива принимается за растяжимую нить
Если принимать тетиву за растяжимую нить, то при смещении тетивы и накоплении потенциальной энергии будет отличен от вычисленного для нерастяжимой нити. Также изменится угол отклонения плеч от положения, рассматриваемого в качестве начального - когда тетива натянула на лук и не деформирована стрелком. В следствие изменения изменится и плечо силы натяжения тетивы. Так, изменится вся величина силы.
Сила натяжения нити: , где величина p - длина тетивы в натянутом состоянии, а - длина тетивы в положении, рассматриваемом в качестве начального
Для вычисления длины нити в промежуточный момент времени мы введем систему из трех уравнений. Первое уравнение заключается в обобщенной теореме Пифагора,второе уравнение получается из рассмотрения статического равновесия в середине тетивы (месте приложения силы, действующей на стрелу), а третье из рассмотрения положения статического равновесия системы тетива - плечо лука в некоторый момент времени.
Итак,
Так,
, с другой стороны,
Так, получаем, что
Решение системы получается весьма нетривиальным, а потому можно прибегнуть к упрощению полученного уравнения для величины угла смещения плеч. Упрощение происходит посредством отбрасывания малых величин.
Уравнение для силы, действующей на стрелу, выглядит следующим образом:
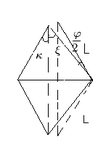
Случай малых углов
Рассмотрим случай, когда смещение тетивы от положения равновесия мало, то есть и малы.
Выразим величину через малые углы.
Выразим малые углы через известные:
Итак,
Сила, прикладываемая к середине тетивы, в таком случае выражается следующим образом:
Дальность же полета окажется равной:
Небольшое исследование зависимостей в полученной модели
Интегрирование полученного выражения для силы натяжения тетивы по смещению даст следующее выражение для мощности:
Поскольку , получаем, что
Нахождение изгибающего момента в сечении плеча лука
Обсуждение результатов и выводы[править]
Одним из основных вопросов, влияющих на вычисления, было выявление характера зависимости прикладываемой к тетиве силы от смещения тетивы. Из ранее проведенного опыта (Искусство стрельбы из лука. Фролова Ксения.(скачать презентацию: ppt, 1.09 MB)) можно наглядно увидеть динамическую кривую (изображение данной характеристики на графике) простого прямого лука (ролевого с текстолитовыми плечами), имеющегося в наличии, а также из проделанной работы по классификации различных модификаций обсуждаемого метательного оружия можно выделить для рассмотрения динамические кривые опять же прямого прямого лука, рекурсивного лука и современного блочного лука. Вычисления в рамках данной курсовой работы велись для наиболее простой модели лука - прямого лука, плечи которого в состоянии без тетивы представляют собой прямую палку. Полученная зависимость оказалось отнюдь нелинейной. Оказалось, что прикладываемая к тетиве сила зависит от куба величины смещения тетивы, от квадрата величины длины плеча лука, от квадрата величины начального смещения тетивы (когда тетива одета на лук, к которому не прикладывается сила), от жесткости материала, из которого сделаны плечи лука.
Также в качестве исследования нужно было рассмотреть тетиву как нерастяжимую нить и как растяжимую, выяснив, что более влияет на полет стрелы при спуске - сила упругости плеч или же тетивы лука. Полученные результаты показали, что величина силы, действующей на стрелу при спуске различна для этих случаев. В следствие этого можно сделать вывод, что пренебрегать удлинением нити не следует.
Используя полученную модель лука, мы четко видим поведение стрелы в предельных случаях. При стрельбе из лука в горизонтальном направлении мы получаем нулевую дальность, равно, как и при вертикальной стрельбе. Реально же дальность полета снаряда зависит от высоты человека (расстояния от земли до уровня середины тетивы, в месте которой прикладывается сила). Также из полученной модели видно, что при малых углах (малом оттягивании тетивы от положения равновесия), дальность полета - малая величина. При обращении же величины смещения тетивы в ноль, дальность полета оказывается также равной нулю, то есть, полета стрелы не будет.
Ссылки по теме[править]
- Искусство стрельбы из лука. Фролова Ксения.(скачать презентацию: ppt, 1.09 MB)
- Энергия метательного снаряда
- Луки и стрелы, современные и древние