Ковалев Олег. Курсовой проект по теоретической механике — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
(→‎Обсуждение результатов и выводы)
 
(не показана 51 промежуточная версия 3 участников)
Строка 1: Строка 1:
 
== Тема проекта ==
 
== Тема проекта ==
  
−
Вычисление энергии напряженного состояния у платоновых углеводородов
+
Вычисление энергии напряженного состояния для платоновых углеводородов
  
 
== Постановка задачи ==
 
== Постановка задачи ==
Строка 10: Строка 10:
  
 
* Тетраэдран
 
* Тетраэдран
−
Представляет собой химическое соединение С4H4, в котором атомы углерода расположены в вершинах тетраэдра. Длина связи C-C равна 0,1522 нм, С-H равна 0,1068 нм. Энергия связи, полученная аналитически, равна 3,90 эВ/атом [3]. Проблема синтеза остается нерешенной.
+
Представляет собой химическое соединение <math>C_4H_4</math>, в котором атомы углерода расположены в вершинах тетраэдра. Длина связи C-C равна 0,1522 нм, С-H равна 0,1068 нм. Проблема синтеза остается нерешенной.
 
[[Файл:Tetraedran.jpg|thumb|справа|150px|Tetraedran]]
 
[[Файл:Tetraedran.jpg|thumb|справа|150px|Tetraedran]]
  
 
*Кубан
 
*Кубан
−
Представляет собой химическое соединение С8H8, в котором атомы углерода расположены в вершинах куба. Длина связи C-C равна 0,157 нм, C-H равна 0,1082. Энергия связи, полученная экспериментально, равна 4,47 эВ/атом [1]. Синтезированы.
+
Представляет собой химическое соединение <math>C_8H_8</math>, в котором атомы углерода расположены в вершинах куба. Длина связи C-C равна 0,157 нм, C-H равна 0,1082. Синтезированы.
 
[[Файл:Cubane.jpg|thumb|справа|150px|Cubane]]
 
[[Файл:Cubane.jpg|thumb|справа|150px|Cubane]]
  
 
* Додекаэдран
 
* Додекаэдран
−
Представляет собой химическое соединение С20H20, в котором атомы углерода расположены в вершинах додекаэдра. Синтезированы.
+
Представляет собой химическое соединение <math>C_{20}H_{20}</math>, в котором атомы углерода расположены в вершинах додекаэдра. Синтезированы.
 
[[Файл:Dodecahedrane.jpg|thumb|справа|150px|Dodecahedrane]]
 
[[Файл:Dodecahedrane.jpg|thumb|справа|150px|Dodecahedrane]]
  
 
== Решение ==
 
== Решение ==
  
−
Рассмотрим следующую модель молекулы. Предположим, что связи между C-C можно заменить линейными пружинками жесткости <math>к = 660 H/м</math> (соответствует графиту). Также, предположим, что связи C-C и С-С скреплены угловыми пружинками жесткости <math> с = 101 H*м</math> (соответствует алмазу). Тогда, в силу симметрии молекул, можно записать простые соотношение для энергии.
+
Существует три подхода расчета энергии напряжения: экспериментальный, основанный на вычислении тепловой энергии, образующейся при сжигании материала; приближенные квантовохимические расчеты; методом расчета механической модели молекулы [6]. В данной работе используется третий подход.
 +
 
 +
Рассмотрим следующую модель молекулы. Предположим, что связи между C-C можно заменить линейными пружинами жесткости <math> k = 660 H/m</math> (соответствует графиту). Также, предположим, что связи C-C и С-С скреплены угловыми пружинами жесткости <math> c = 1,35\cdot 10^{-18} H\cdot m</math> (соответствует алмазу). Тогда упрощенное уравнение расчета энергии напряжения в рамка механической модели будет иметь следующий вид [5]:
 +
 
 +
<math>
 +
U=1/2kn_a(a - a_0)^2 + 1/2cn_\alpha(sin^2(\alpha - \alpha_0)),
 +
</math>
 +
 
 +
Здесь каждое слагаемое относится к отдельным компонентам напряжения: деформациям расстояний (<math>a</math>) и валентных углов <math>\alpha</math>.
 +
Тогда, в силу симметрии молекул, можно записать простые соотношение для энергии.
  
 
* Для тэтраэдрана
 
* Для тэтраэдрана
  
 
<math>
 
<math>
−
U_t=3k(a - a_0)^2 + 6c(cos^2(\alpha - \alpha_0)),
+
U_t=3k(a - a_0)^2 + 6c(sin^2(\alpha - \alpha_0)),
 
</math>
 
</math>
  
−
где <math>\alpha = 60^0</math> - угол между связями C-C и С-H в молекуле тетраэдрана, <math>\alpha_0 = 109,5^0</math> - угол между С-С и С-H, в недеформированном состоянии; <math>a</math> - длина связи С-С в молекуле тетраэдрана, <math>a_0</math> - длина связи C-C в алканах.
+
где <math>\alpha = 60^0</math> - валентный угол в молекуле тетраэдрана, <math>\alpha_0 = 109,5^0</math> - валентный угол в недеформированном состоянии; <math>a</math> - длина связи С-С в молекуле тетраэдрана, <math>a_0</math> - длина связи C-C в алканах.
  
 
* Для кубана
 
* Для кубана
  
 
<math>
 
<math>
−
U_k=6k(a - a_0)^2 + 12c(cos^2(\alpha - \alpha_0)),
+
U_k=6k(a - a_0)^2 + 12c(sin^2(\alpha - \alpha_0)),
 
</math>
 
</math>
  
−
где <math>\alpha = 90^0</math> - угол между связями C-C и С-H в молекуле кубана, <math>\alpha_0 = 109,5^0</math> - угол между С-С и С-H, в недеформированном состоянии; <math>a</math> - длина связи С-С в молекуле кубана, <math>a_0</math> - длина связи C-C в алканах.
+
где <math>\alpha = 90^0</math> - валентный угол в молекуле кубана, <math>\alpha_0 = 109,5^0</math> - валентный угол в недеформированном состоянии; <math>a</math> - длина связи С-С в молекуле кубана, <math>a_0</math> - длина связи C-C в алканах.
  
 
* Для додекаэдрана
 
* Для додекаэдрана
  
 
<math>
 
<math>
−
U_d=15k(a - a_0)^2 + 30c(cos^2(\alpha - \alpha_0)),
+
U_d=15k(a - a_0)^2 + 30c(sin^2(\alpha - \alpha_0)),
 
</math>
 
</math>
  
−
где <math>\alpha = 108^0</math> - угол между связями C-C и С-H в молекуле додекаэдрана, <math>\alpha_0 = 109,5^0</math> - угол между С-С и С-H, в недеформированном состоянии; <math>a</math> - длина связи С-С в молекуле додекаэдрана, <math>a_0</math> - длина связи C-C в алканах.
+
где <math>\alpha = 108^0</math> - валентный угол между в молекуле додекаэдрана, <math>\alpha_0 = 109,5^0</math> - валентный угол в недеформированном состоянии; <math>a</math> - длина связи С-С в молекуле додекаэдрана, <math>a_0</math> - длина связи C-C в алканах.
  
 
== Обсуждение результатов и выводы ==
 
== Обсуждение результатов и выводы ==
 +
 +
{| class="wikitable"
 +
|-
 +
!'''Молекула'''
 +
!'''Длина связи, nm'''
 +
!'''Валентный угол'''
 +
!'''Энергия напряжения, kcal/mol'''
 +
|-
 +
| Тэтраэдран
 +
| <center><math>0.152</math></center>
 +
| <center><math>60.0^0</math></center>
 +
| <center><math>676.0</math></center>
 +
|-
 +
| Кубан
 +
| <center><math>0.157</math></center>
 +
| <center><math>90.0^0</math></center>
 +
| <center><math>265.3</math></center>
 +
|-
 +
| Додекаэдран
 +
| <center><math>0.154</math></center>
 +
| <center><math>108.0^0</math></center>
 +
| <center><math>4.0</math></center>
 +
|-
 +
| Алмаз
 +
| <center><math>0.154</math></center>
 +
| <center><math>109.5^0</math></center>
 +
| <center><math>0.0</math></center>
 +
|}
 +
 +
{| class="wikitable"
 +
|-
 +
!'''Вещество'''
 +
!'''Энергия, выделяемая при сгорании (разложении) вещества, мДж/кг'''
 +
|-
 +
| Водород
 +
| <center><math>120.9</math></center>
 +
|-
 +
| Бензин
 +
| <center><math>42-43</math></center>
 +
|-
 +
| Тэтраэдран
 +
| <center><math>35.2</math></center>
 +
|-
 +
| Кубан
 +
| <center><math>27.6</math></center>
 +
|-
 +
| Тротил
 +
| <center><math>4.2</math></center>
 +
|-
 +
| Порох
 +
| <center><math>3.8</math></center>
 +
|-
 +
| Додекаэдран
 +
| <center><math>1.0</math></center>
 +
|}
 +
 +
В результате работы были вычислены энергии напряжения для тетраэдрана, кубана и додекаэдрана (значения приведены в таблице).
 +
Из таблицы видно, что с ростом валентного угла, растет энергия напряжения. Это связано с тем, что основной вклад в энергию вносят деформации валентных углов (у додекаэдрана наименьшая, у тетраэдрана наибольшая). Вклад межатомных связей мал, так как мала их деформация. Значение энергии для кубана отличается от значения 150 kcal/mol, приведенного в работе [6] на 43%, однако в работе не указан способ получения данного значения.
  
 
== Ссылки по теме ==  
 
== Ссылки по теме ==  
  
−
* Термическая устойчивость кубана C8H8. М.М. Маслов, Д.А. Лобанов, А.И. Подливаев, Л.А. Опенов. http://journals.ioffe.ru/ftt/2009/03/p609-612.pdf
+
* 1. Термическая устойчивость кубана C8H8. М.М. Маслов, Д.А. Лобанов, А.И. Подливаев, Л.А. Опенов. http://journals.ioffe.ru/ftt/2009/03/p609-612.pdf
−
* Термическая устойчивость линейных олигомеров, построенных из кубиленовых единиц. М.М. Маслов. http://journals.ioffe.ru/ftt/2009/03/p609-612.pdf
+
* 2. Термическая устойчивость линейных олигомеров, построенных из кубиленовых единиц. М.М. Маслов. http://journals.ioffe.ru/ftt/2009/03/p609-612.pdf
−
* Термическая устойчивость молекулы тетраэдрана C4H4. М.М. Маслов.
+
* 3. Термическая устойчивость молекулы тетраэдрана C4H4. М.М. Маслов.
−
 
+
* 4. Description of elastic properties of diamond using angular atomic interaction. S. S. Khakalo A. M. Krivtsov O. S. Loboda.
 +
* 5. Энергия напряжения, геометрическое строение и контакты спин - спинового взаимодействия циклических углеводородов. Козина М. П., Мастрюков В. С, Мильвицкая Ε. М. http://www.uspkhim.ru/php/getFT.phtml?jrnid=rc&paperid=2906&year_id=1982
 +
* 6. Vibrations of the cubane molecule: inelastic neutron scattering study and theory. T. Yildirim. Kılıc, S. Ciraci, P.M. Gehring, D.A. Neumann, P.E. Eaton, T. Emrick. http://webster.ncnr.nist.gov/instruments/fans/fans_pdf_files/yildirim1999.pdf
 +
*[[Ковалев Олег. Проект "Фуллерены С20 и С60".|"Фуллерены С20 и С60"]]
  
 
== См. также ==
 
== См. также ==
Строка 64: Строка 134:
 
* [[Кафедра "Теоретическая механика"]]
 
* [[Кафедра "Теоретическая механика"]]
 
* [[Ковалев Олег]]
 
* [[Ковалев Олег]]
−
 
  
 
[[Category: Студенческие проекты]]
 
[[Category: Студенческие проекты]]

Текущая версия на 13:44, 27 июня 2012

Тема проекта[править]

Вычисление энергии напряженного состояния для платоновых углеводородов

Постановка задачи[править]

Рассчитать энергию напряженного состояния для молекул тетраэдрана, кубана и додекаэдрана.

Общие сведения о платоновых углеводородах[править]

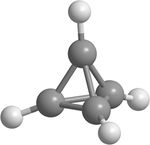
  • Тетраэдран

Представляет собой химическое соединение [math]C_4H_4[/math], в котором атомы углерода расположены в вершинах тетраэдра. Длина связи C-C равна 0,1522 нм, С-H равна 0,1068 нм. Проблема синтеза остается нерешенной.

Tetraedran
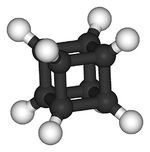
  • Кубан

Представляет собой химическое соединение [math]C_8H_8[/math], в котором атомы углерода расположены в вершинах куба. Длина связи C-C равна 0,157 нм, C-H равна 0,1082. Синтезированы.

Cubane
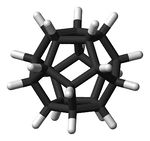
  • Додекаэдран

Представляет собой химическое соединение [math]C_{20}H_{20}[/math], в котором атомы углерода расположены в вершинах додекаэдра. Синтезированы.

Dodecahedrane

Решение[править]

Существует три подхода расчета энергии напряжения: экспериментальный, основанный на вычислении тепловой энергии, образующейся при сжигании материала; приближенные квантовохимические расчеты; методом расчета механической модели молекулы [6]. В данной работе используется третий подход.

Рассмотрим следующую модель молекулы. Предположим, что связи между C-C можно заменить линейными пружинами жесткости [math] k = 660 H/m[/math] (соответствует графиту). Также, предположим, что связи C-C и С-С скреплены угловыми пружинами жесткости [math] c = 1,35\cdot 10^{-18} H\cdot m[/math] (соответствует алмазу). Тогда упрощенное уравнение расчета энергии напряжения в рамка механической модели будет иметь следующий вид [5]:

[math] U=1/2kn_a(a - a_0)^2 + 1/2cn_\alpha(sin^2(\alpha - \alpha_0)), [/math]

Здесь каждое слагаемое относится к отдельным компонентам напряжения: деформациям расстояний ([math]a[/math]) и валентных углов [math]\alpha[/math]. Тогда, в силу симметрии молекул, можно записать простые соотношение для энергии.

  • Для тэтраэдрана

[math] U_t=3k(a - a_0)^2 + 6c(sin^2(\alpha - \alpha_0)), [/math]

где [math]\alpha = 60^0[/math] - валентный угол в молекуле тетраэдрана, [math]\alpha_0 = 109,5^0[/math] - валентный угол в недеформированном состоянии; [math]a[/math] - длина связи С-С в молекуле тетраэдрана, [math]a_0[/math] - длина связи C-C в алканах.

  • Для кубана

[math] U_k=6k(a - a_0)^2 + 12c(sin^2(\alpha - \alpha_0)), [/math]

где [math]\alpha = 90^0[/math] - валентный угол в молекуле кубана, [math]\alpha_0 = 109,5^0[/math] - валентный угол в недеформированном состоянии; [math]a[/math] - длина связи С-С в молекуле кубана, [math]a_0[/math] - длина связи C-C в алканах.

  • Для додекаэдрана

[math] U_d=15k(a - a_0)^2 + 30c(sin^2(\alpha - \alpha_0)), [/math]

где [math]\alpha = 108^0[/math] - валентный угол между в молекуле додекаэдрана, [math]\alpha_0 = 109,5^0[/math] - валентный угол в недеформированном состоянии; [math]a[/math] - длина связи С-С в молекуле додекаэдрана, [math]a_0[/math] - длина связи C-C в алканах.

Обсуждение результатов и выводы[править]

Молекула Длина связи, nm Валентный угол Энергия напряжения, kcal/mol
Тэтраэдран
[math]0.152[/math]
[math]60.0^0[/math]
[math]676.0[/math]
Кубан
[math]0.157[/math]
[math]90.0^0[/math]
[math]265.3[/math]
Додекаэдран
[math]0.154[/math]
[math]108.0^0[/math]
[math]4.0[/math]
Алмаз
[math]0.154[/math]
[math]109.5^0[/math]
[math]0.0[/math]
Вещество Энергия, выделяемая при сгорании (разложении) вещества, мДж/кг
Водород
[math]120.9[/math]
Бензин
[math]42-43[/math]
Тэтраэдран
[math]35.2[/math]
Кубан
[math]27.6[/math]
Тротил
[math]4.2[/math]
Порох
[math]3.8[/math]
Додекаэдран
[math]1.0[/math]

В результате работы были вычислены энергии напряжения для тетраэдрана, кубана и додекаэдрана (значения приведены в таблице). Из таблицы видно, что с ростом валентного угла, растет энергия напряжения. Это связано с тем, что основной вклад в энергию вносят деформации валентных углов (у додекаэдрана наименьшая, у тетраэдрана наибольшая). Вклад межатомных связей мал, так как мала их деформация. Значение энергии для кубана отличается от значения 150 kcal/mol, приведенного в работе [6] на 43%, однако в работе не указан способ получения данного значения.

Ссылки по теме[править]

См. также[править]

Источник — «http://tm.spbstu.ru/?title=Ковалев_Олег._Курсовой_проект_по_теоретической_механике&oldid=13193»