Веренинов Игорь. Курсовой проект по теоретической механике — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
Строка 12: Строка 12:
 
Составим соотношение скоростей при движении по эллиптической траектории. Скорость всегда направлена по касательной к пути, обозначим за <math>\gamma</math> угол между скоростью и радиус-вектором из фокуса.
 
Составим соотношение скоростей при движении по эллиптической траектории. Скорость всегда направлена по касательной к пути, обозначим за <math>\gamma</math> угол между скоростью и радиус-вектором из фокуса.
  
−
<math>Vsin\gamma =\omega r \mid\cdot r</math>
+
<math>V\sin\gamma =\omega r \mid\cdot r</math>
  
 
По 2-ому закону Кепплера, площадь отсекаемая радиус-вектором за единицу времени постоянна.
 
По 2-ому закону Кепплера, площадь отсекаемая радиус-вектором за единицу времени постоянна.
  
−
<math>rVsin\gamma =\omega r^2=const</math>
+
<math>rV\sin\gamma =\omega r^2=const</math>
  
−
<math>r_{1}V_{1}sin\gamma_{1} =r_{2}V_{2}sin\gamma_{2} </math>
+
<math>r_{1}V_{1}\sin\gamma_{1} =r_{2}V_{2}\sin\gamma_{2} </math>
  
 
В точках А и В
 
В точках А и В
  
−
<math>sin\gamma_{1}=sin\gamma_{2}=1</math>
+
<math>\sin\gamma_{1}=\sin\gamma_{2}=1</math>
  
 
<math>V_{2}=\frac{R_{1}V_{1}}{R_{2}}</math>
 
<math>V_{2}=\frac{R_{1}V_{1}}{R_{2}}</math>
Строка 33: Строка 33:
  
 
<math> V_{1}=\sqrt{\frac{2GMR_{2}}{R_{1}(R_{2}+R_{1})}}</math>
 
<math> V_{1}=\sqrt{\frac{2GMR_{2}}{R_{1}(R_{2}+R_{1})}}</math>
 +
 +
Разложим в ряд  до второго порядка с заменой
 +
 +
<math> R_{2}=R_{1}+dR </math>
 +
 +
<math>dR \ll R1 </math>
 +
 +
<math> V_{1}=\sqrt{2GM}\frac{R_{2}}{dR} </math>
 +
 +
<math> \sqrt{2GM}=2.8238*10^7 </math>
  
 
Скорость тела на геостационарной орбите
 
Скорость тела на геостационарной орбите

Версия 23:07, 31 мая 2012

Тема проекта

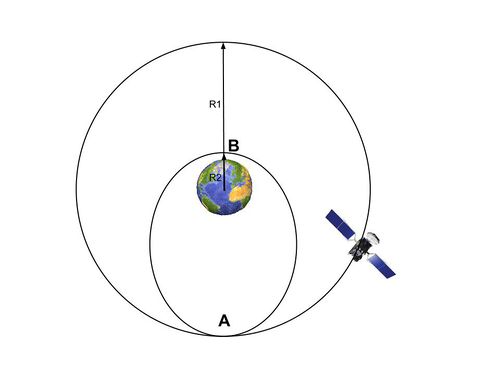
Расчет траектории схода спутника с геостационарной орбиты.

Постановка задачи

Задача связана с решение проблемы космического мусора: множество спутников, выработавовших свой ресурс, вращаются по орбите представляя опасность для других аппаратов. Требуется рассчитать по какой траектории должен лететь спутник, чтобы попасть в атмосферу и какая энергия требуется для торможения.

Решение

Untitled drawing (1).jpg

Составим соотношение скоростей при движении по эллиптической траектории. Скорость всегда направлена по касательной к пути, обозначим за [math]\gamma[/math] угол между скоростью и радиус-вектором из фокуса.

[math]V\sin\gamma =\omega r \mid\cdot r[/math]

По 2-ому закону Кепплера, площадь отсекаемая радиус-вектором за единицу времени постоянна.

[math]rV\sin\gamma =\omega r^2=const[/math]

[math]r_{1}V_{1}\sin\gamma_{1} =r_{2}V_{2}\sin\gamma_{2} [/math]

В точках А и В

[math]\sin\gamma_{1}=\sin\gamma_{2}=1[/math]

[math]V_{2}=\frac{R_{1}V_{1}}{R_{2}}[/math]

Подставляем в закон сохранения энергии

[math]V_{1}^2-\frac{R_{1}^2V_{1}^2}{R_{2}^2}=2GM\left(\frac{1}{R_{1}}-\frac{1}{R_{2}} \right )[/math]

Получаем скорость, которую должно иметь тело в точке А для попадания в В

[math] V_{1}=\sqrt{\frac{2GMR_{2}}{R_{1}(R_{2}+R_{1})}}[/math]

Разложим в ряд до второго порядка с заменой

[math] R_{2}=R_{1}+dR [/math]

[math]dR \ll R1 [/math]

[math] V_{1}=\sqrt{2GM}\frac{R_{2}}{dR} [/math]

[math] \sqrt{2GM}=2.8238*10^7 [/math]

Скорость тела на геостационарной орбите

[math] V_{orbit}=\sqrt{\frac{GM}{R_{1}}} [/math]

Теперь рассчитаем затраты энергии на совершение торможения.

[math] E=\frac{mV_{\delta}^2}{2} [/math]

[math] V_{\delta}=\sqrt{\frac{GM}{R_{1}}} - \sqrt{\frac{2GMR_{2}}{R_{1}(R_{2}+R_{1})}} [/math]


Обсуждение результатов и выводы

В приведенные формулы были подставлены значения для спутника вращающегося на 300 км орбите и имеющего массу 10 кг. Для того чтобы его траектория прошла через атмосферу потребовалось бы 20МДж, что соответствует сгоранию 2кг бензина в воздухе. Потребовалось бы снизить скорость до 5.65 км/c .

Ссылки по теме

См. также

Источник — «http://tm.spbstu.ru/?title=Веренинов_Игорь._Курсовой_проект_по_теоретической_механике&oldid=12524»